В финансовой деятельности при значительных размерах задолженности долг обычно погашается в рассрочку, частями. Такой метод погашения часто называют амортизацией долга.
Есть два способа погашения долга в рассрочку:
1) погашение основного долга равными суммами (долями);
2) погашение всей задолженности равными или переменными суммами по обслуживанию долга (срочными уплатами).
Погашение основного долга равными суммами. Пусть долг в размере D погашается в течение n лет. В этом случае сумма, ежегодно идущая на его погашение, составит:
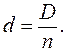
Размер долга последовательно сокращается: D, D – d, D – 2d и т.д. Соответственно уменьшаются и выплачиваемые проценты, так как они начисляются на остаток долга. Пусть проценты выплачиваются раз в конце года по ставке g. Тогда за первый и последующие годы они равны Dg,(D – d)g,(D – 2d)g и т.д.
Срочная уплата в конце первого года находится как:
Y1= D×g + d.
Для конца года t находим:
Yt = Dt-1×g + d, t = 1,…, n, (9.5)
где Dt – остаок долга на конец года t.
Остаток долга можно определять последовательно:
.
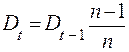Если долг погашается p раз в году постнумерандо и с такой же частотой выплачиваются проценты, каждый раз по ставке g/p, то срочная уплата составит:
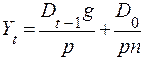, t = 1,…, pn. (9.6)
Остаток задолженности на конец года t в этом случае составит:
.
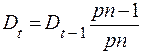Пример 9.3. Разработать план погашения долга в сумме 1000 тыс.руб., который необходимо погасить последовательными равными суммами за 5 лет платежами постнумерандо. За заем выплачиваются 10% годовых, погашение и начисление процентов раз в год.
Решение. 1) Размер погашения основного долга:
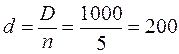тыс. руб. в год.
2) Ежегодные процентные платежи составят:
I1 = 1000×0,1 = 100 тыс. руб.;
I2 = (1000 – 200)×0,1 = 80 тыс. руб. и т.д.
План погашения представим в виде табл. 9.2.
Таблица 9.2
| Год | Остаток долга на начало года | Проценты | Погашение долга | Расходы по займу |
Как видно, последовательно уменьшаются как расходы по займу, так и соотношения процентов и суммы основного долга. ·
Пример 9.4.Продолжим пример 9.3. Пусть проценты начисляются ежеквартально, а погашаются раз в год. Остальные условия сохраняются. В этом случае ежегодные процентные платежи составят:
I1 = (1000×0,1)/4 = 25 тыс. руб. в квартал.
I2 = [(1000 – 200)×0,1]/4 = 20 тыс. руб. и т.д.
План погашения представим в виде табл. 9.3.
Таблица 9.3
| Год | Квартал | Остаток долга на начало года | Проценты | Погашение долга | Расходы по займу |
| 1 кв. | - | ||||
| 2 кв. | - | ||||
| 3 кв. | - | ||||
| 4 кв. | |||||
| 1 кв. | - | ||||
| 2 кв. | - | ||||
| 3 кв. | - | ||||
| 4 кв. | |||||
| 1 кв. | - | ||||
| 2 кв. | - | ||||
| 3 кв. | - | ||||
| 4 кв. | |||||
| 1 кв. | - | ||||
| 2 кв. | - | ||||
| 3 кв. | - | ||||
| 4 кв. |
Окончание табл. 9.3
| Год | Квартал | Остаток долга на начало года | Проценты | Погашение долга | Расходы по займу |
| 1 кв. | - | ||||
| 2 кв. | - | ||||
| 3 кв. | - | ||||
| 4 кв. |
Рассмотренный метод амортизации отличается простотой расчетов, но часто является нежелательным для должника, так как в начале срока срочные уплаты погашения выше, чем в конце его.
Погашение долга равными срочными уплатами. В соответствии с этим методом расходы должника по обслуживанию долга постоянны на протяжении всего срока погашения. Из общей суммы расходов должника часть идет на уплату процентов, остаток – на погашение основного долга. По определению:
Y = Dt-1×g + Rt = const,
где Dt-1×g – проценты по долгу; Rt – сумма выплаты основного долга.
План погашения обычно разрабатывается для двух случаев:
а) если задан срок погашения долга;
б) заданы расходы по обслуживанию долга.
Рассмотрим оба случая.
А) Задан срок погашения. Первый этап разработки плана погашения – определение размера срочной уплаты. Далее полученная величина разбивается на процентные платежи и сумму, идущую на погашение долга. После чего определяется остаток задолженности.
Периодическая выплата постоянной суммы Y равнозначна ренте с заданными параметрами, или:
, 
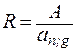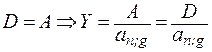, (9.7)
где an;g – коэффициент приведения годовой ренты со ставкой g и сроком n.
Все величины, необходимые для разработки плана, можно рассчитать на основе величины Y и данных финансового контракта. Найдем сумму первого погасительного платежа:
d1= Y – D×g,
…………….
dt = dt-1 (1+g). (9.8)
Платежи по погашению долга образуют ряд d1, d1 (1+g), ……., d1 (1+g)n-1. По этим данным можно определить сумму погашенной задолженности на конец года t после очередной выплаты:
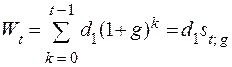, (9.9)
где st;g – коэффициент наращения постоянной ренты постнумерандо.
Пример 9.5.Сумму долга в 1 млн. руб. необходимо погасить в течение 4 лет равными срочными уплатами. Срочные уплаты производятся в конце каждого года. Проценты на долг начисляются по ставке 12% годовых. Составить план погашения долга.
Решение. 1) Ежегодные срочные уплаты по погашению долга вычисляются по формуле (9.7):
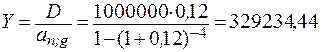руб.
2) Значение выплаты в конце первого года определяется соотношением (9.8):
d1= Y – D×g = 329234 – 1000000×0,12 = 209234,44 руб.
3) Проценты в конце первого года:
I1 = 1000000×0,12 = 120 000 руб.
4) Остаток долга после первого погашения:
D1 = 1000000 – 209234 = 790765,56 руб.
5) Отсюда I2 = 790765,56×0,12 = 94891,87 руб. и т.д.
План погашения представим в виде табл. 9.4.
Таблица 9.4
| Год | Остаток долга на начало года | Расходы по займу | Проценты | Погашение долга |
| 1 000 000 | 329 234,44 | 120 000 | 209 234,44 | |
| 790 765,56 | 329 234,44 | 94 891,87 | 234 342,57 | |
| 556 422,99 | 329 234,44 | 66 770,77 | 262 463,67 | |
| 293 959,32 | 329 234,44 | 35 275,12 | 293 959,32 |
Процентные платежи уменьшаются во времени, а суммы погашения основного долга систематически увеличиваются. ·
Аналогичным образом разрабатываются планы погашения и для случаев, когда выплата процентов и погашение основного долга производятся не один, а несколько раз в году:
.
.
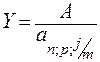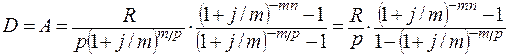Б) Заданы расходы по обслуживанию долга. Решение данной задачи заключается в определении срока погашения долга и достижении полной сбалансированности платежей.
Срок погашения находится как срок постоянной ренты. Пусть выплаты производятся раз в году постнумерандо, тогда применим формулу из табл. 7.1 (стр. 64), где символ R заменен на Y, а i – на g:
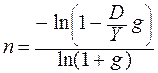. (9.10)
Пример 9.6. Долг равен 1000 тыс. руб. и выдан под 10% годовых. Для его погашения предполагается выделять сумму порядка 200 тыс. руб. в год. Оценим величину срока, необходимого для погашения задолженности:
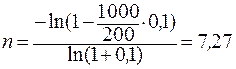года.
Округлим расчетный срок до 7 лет. Для того, чтобы полностью рассчитаться, необходимо несколько повысить срочные уплаты:
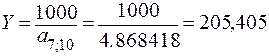тыс. руб.
Альтернативой является адекватная компенсация недостающего покрытия долга при выплате ренты с членом 200 тыс. руб. и сроком 7 лет. ·
Погашение задолженности с использованием переменных расходов по займу. В ситуациях, когда погашение долга связано с поступлением средств из каких либо источников, удобнее погашать долг переменными расходами (выгодно должнику).
Есть два варианта работы с переменными расходами:
1. срочные уплаты образуют ряд, члены которого задаются заранее (график погашения);
2. срочные уплаты образуют ряд, члены которого следуют какому либо формальному закону (прогрессии, заданной функции).
Пусть ряд срочных уплат представляет собой геометрическую прогрессию со знаменателем q, тогда этот ряд можно записать в виде членов переменной ренты Y, Yq, Yq2, …, Yqn-1. Приравняв современную стоимость этой ренты сумме первоначального долга, находим:
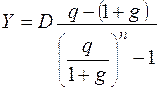, (9.11)
где q = 1+k – годовой темп роста платежей, k – темп прироста, g – процентная ставка по займу.
Далее находятся срочные уплаты и разрабатывается детальный план погашения.
Пример 9.7.Пусть расходы по займу (сумма долга – 1000 тыс. руб.) уменьшаются каждый год на 10%; общий срок погашения 5 лет, ставка процента по долгу – 6% годовых. Определить срочную уплату и составить план погашения долга.
Решение. D = 1000 тыс. руб., n = 5 лет, g = 6%, q = 1 – k = 0,9. Согласно формуле (9.11) срочная уплата составит:
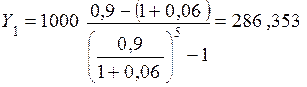тыс. руб.
Отсюда определим остаток долга:
I1 = 1000×0,06 = 60 тыс. руб.
d1 = 286,353 – 60 = 226,353 тыс. руб.
D2 = 1000 – 226,353 = 773,647 тыс. руб.
Y1 = Y1× 0,9t-1 – расчет срочной уплаты для 1-го года, Yt = Yt-1×0,9 – для 2-го и последующих лет.
План погашения долга представлен в табл. 9.5.
Таблица 9.5
| Год | Остаток долга на начало года | Расходы по займу | Проценты | Погашение долга |
| 1000,000 | 286,353 | 60,000 | 226,353 | |
| 773,667 | 257,717 | 46,419 | 211,298 | |
| 562,349 | 231,946 | 33,741 | 198,205 | |
| 364,144 | 208,751 | 21,849 | 186,902 | |
| 177,241 | 187,875 | 10,634 | 177,241 |
В ряде случаев размеры срочной уплаты связываются с ожидаемыми поступлениями средств и задаются заранее в виде графика погашения. Размер последней срочной уплаты не задается. Она определяется как сумма остатка долга на начало последнего периода.
Пример 9.8.Долг в размере 100 000 руб. решено погасить по специальному графику за 4 года – суммы расходов по погашению долга по годам: 40, 20 и 30 тыс. руб. Остаток выплачивается в конце четвертого года. Ставка процента по долгу установлена в размере 10% годовых. Разработать план погашения.
Решение.
План погашения долга представлен в табл. 9.6.
Таблица 9.6
| Год | Остаток долга на начало года | Расходы по займу | Проценты | Погашение долга |
| 100 000 | 40 000 | 10 000 | 30 000 | |
| 70 000 | 20 000 | 13 000 | ||
| 57 000 | 30 000 | 24 300 | ||
| 32 700 | 35 970 | 32 700 |
Льготные займы и кредиты
В ряде случаев долгосрочные займы и кредиты выдаются по тем или иным причинам под льготные для заемщика условия. Низкая (относительно ставки на рынке кредитов) процентная ставка в сочетании с большим его сроком и льготным периодом дают должнику существенную выгоду, которую можно рассматривать как субсидию. Кредитор в этих условиях несет некоторые потери, так как он мог бы инвестировать деньги на более выгодных условиях.
Льготные займы главным образом используются при оказании международными организациями финансовой помощи ряду развивающихся стран.
Грант-элемент – это условная потеря кредитора, которая связана с применением более низкой процентной ставки, чем существующие ставки кредитного рынка.
Грант-элемент определяется в абсолютной и относительной величинах.
Абсолютный грант-элемент рассчитывается как разность номинальной суммы займа и современной величины платежей по погашению займов, рассчитанной по рыночной ставке. Обычно используют ставку, превалирующую на рынке долгосрочных кредитов.
Размер абсолютного грант-элемента находим следующим образом:
W = D – A, (9.12)
где W – абсолютный грант-элемент, D – сумма долга, A – современная стоимость платежей, поступающих в счет погашения займа, рассчитанная по реальной ставке кредитного рынка.
Относительный грант-элемент характеризует отношение абсолютного грант-элемента к сумме займа:
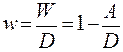, (9.13)
где w – относительный грант-элемент.
Выведем рабочие формулы для расчета W и w при условии, что долг и проценты выплачиваются в виде постоянных срочных уплат.
Пусть займ выдан на n лет и предусматривает выплату процентов по ставке g. На денежном рынке аналогичные по сроку и величине займы выдаются по ставке r. В этом случае при отсутствии льготного периода срочная уплата составит:
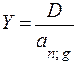, (9.14)
а современная величина всех выплат должника очевидно равна Yan;r. В итоге
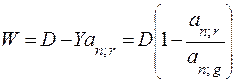, (9.15)
,
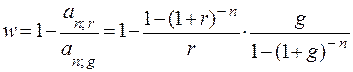где an;r, an;g – коэффициенты приведения постоянных годовых рент постнумерандо, определенные для процентных ставок r и g, r > g.
Пример 9.9.Льготный займ выдан на 10 лет под 3,8%. Предусматривается погашение долга равными срочными уплатами. Известно, что обычная рыночная ставка для такого займа равна 8%. В этом случае
.
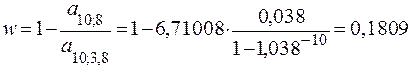Допустим, исходная сумма займа равна 10 млн. руб. Тогда абсолютный грант-элемент или условная сумма потерь для кредитора и, соответственно, выгода для должника, составят:
W = 10 × 0,1809 = 1,809 млн. руб. ·
Наличие льготного периода увеличивает грант-элемент. Если в льготном периоде должник выплачивает проценты, то современная стоимость поступлений по долгу определяется как сумма двух элементов: современных величин процентных платежей в льготном периоде и срочных уплат в оставшееся время. Таким образом,
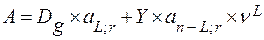, (9.16)
где n – L – продолжительность периода погашения задолженности;
L – продолжительность льготного периода.
После преобразований формулы (9.13) получим:
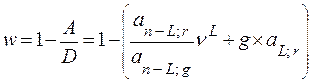, (9.17)
где an-L;r, an-L;g – коэффициенты приведения постоянных рент со сроком n – L лет и ставками r и g;
n L – дисконтный множитель по ставке r.
Рассмотрим еще одни вариант. Пусть в льготном периоде проценты начисляются, но не выплачиваются. Они присоединяются к основному долгу, который погашается в течении n – L лет. Условия такого займа более льготны для должника, чем при последовательной выплате процентов.
Срочные уплаты и их современная величина в данном случае находятся как:
, 
.
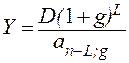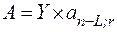На основе этих выражений относительный грант-элемент будет равен:
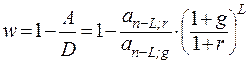. (9.18)
Пример 9.10. Пусть заем в примере 9.9 предусматривает льготный период 3 года, в течение которого выплачиваются проценты. Для расчета относительного грант-элемента находим:
a7;8 = 5,20637, a7;3,8 = 6,04667, a3,8 = 2,5771, n 3 = 1,08–3 = 0,79383.
Подставив в формулу (9.17) получим:
.
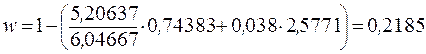Если проценты в льготном периоде не выплачиваются, а присоединяются к основной сумме долга, то
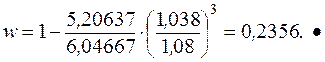
Как было показано выше, грант-элемент – условная обобщающая характеристика льготности займа (потерь кредитора и выигрыша должника). Сумма, которая равна грант-элементу, существенно зависит от принятой при ее определении процентной ставки.
Предельным случаем льготного займа является беспроцентный заем. Выдача такого займа связана с потерями, которые определим, полагая, что соответствующие средства можно было бы разместить под проценты по рыночной ставке r. Например, уже при 15-тилетнем сроке беспроцентного займа и рыночной ставке 10% кредитор теряет 50% от суммы долга.