Аннуитет (рента) пренумерандо
| Наращенная сумма ренты | Современное значение | |
| годовая | ||
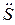 = S (1 + i) = S (1 + i) | Ä = A (1 + i) | |
| годовая, начисление процентов m раз в году | ||
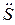 = S (1 + = S (1 + 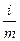 )m )m | Ä = A (1 + 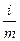 )m )m | |
| p-срочная, начисление процентов один раз в году | ||
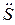 = S (1 + i) = S (1 + i) 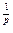 | Ä = A (1 + i) 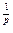 | |
| p-срочная, начисление процентов m раз в году (m = p) | ||
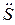 = S (1 + = S (1 + 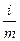 ) ) | Ä = A (1 + 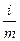 ) ) | |
Пример 23.
В пенсионный фонд ежегодно в начале года вносятся суммы в размере 25 тыс.руб., на которые начисляются сложные проценты по ставке 3% годовых. Определите сумму, накопленную в фонде через 10 лет и сумму начисленных процентов.
Решение:
Рента пренумерандо, годовая, начисление процентов один раз в год. Используем формулу
S = S (1 + i) = 25000 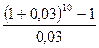
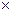 1,03 = 295194 (руб.)
1,03 = 295194 (руб.)
I = 295194 – 25000 = 270194 (руб.)
Исчисление современной стоимости финансовых рент имеет большее практическое значение, чем вычисление наращенной стоимости. Рассмотрим задачу по оценке инвестиционного проекта.
Пример 24.
В течение 4 лет ожидаются поступления от реализации проекта в размере 2 млн. руб. в конце каждого полугодия. Единовременные вложения в проект в начале первого года составили 10 млн. руб. Будут ли данные вложения убыточны или принесут прибыль, при использовании годовой процентной ставки 6%.
Решение:
Поступления в размере 2 млн. руб. ожидаются в течение четырех лет. Поскольку это разновременные выплаты, необходимо привести их к одной дате. Оценим стоимость этих выплат на начало первого года. Для этого используем формулу современной стоимости р-срочной ренты постнумерандо с начислением процентов один раз в году (См. Справочник, Таблица «Аннуитет постнумерандо».)
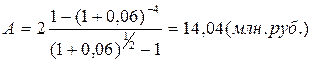
Данный проект можно считать прибыльным, так как вложения 10 млн.руб. обеспечивают ежегодный доход, который на начало первого года оценивается суммой в 14,04 млн. руб.
Теория современной стоимости аннуитета нашла прикладное значение в задачах погашения задолженности равными срочными выплатами. Выше в главе 1 мы уже рассматривали составление плана погашения кредита равными суммами. В данной главе остановимся на задаче погашения задолженности с помощью применения формул финансовой ренты. Экономическая постановка задачи заключается в следующем. Задолженность на начало срока определена в сумме А, ее необходимо погасить равными срочными уплатами R, которые включают в себя начисленные проценты по ставке i. Очевидно, данная задача может быть решена с помощью формул современного значения финансовой ренты.
Пример 25.
Пусть задолженность на текущий момент равна 250000 руб. Долг предлагается погасить в течение 5 лет при использовании процентной ставки 30% годовых. Долг погашается равными срочными уплатами, включающими начисленные проценты Составить план погашения задолженности.
Решение:
Очевидно, что текущая задолженность 250000 руб. представляет собой современную стоимость финансовой ренты с ежегодными платежами R. Рассчитаем срочные выплаты R на основе формулы современного значения годовой ренты постнумерандо (См. Справочник, Таблица «Аннуитет – постнумерандо»).
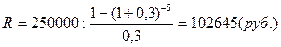
Суммы 102645 руб. выплачиваются в течение пяти лет ежегодно и включают начисленные проценты. Рассчитаем начисленные проценты за первый год:
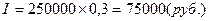
Сумма погашения долга в первом году составляет:
102645-75000=27645 (руб.)
Во втором году остаток долга равен:
250000-27645=222355 (руб.)
На эту сумму во втором году начисляются проценты:

Сумма к погашению во втором году равна:
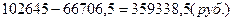
Общий план погашения задолженности можно представить в таблице 2.
Таблица 2.
План погашения задолженности равными срочными выплатами (руб.)
| Год | Остаток на начало года | Погашение долга | Проценты | Срочная выплата |
| 66706,5 | ||||
| 186416,5 | ||||
| 139696,5 | ||||
| Итого: | - | - | - |
Контрольные вопросы
1. Дайте определение финансовой ренты. Назовите параметры ренты.
2. В чем отличие ренты постнумерандо от ренты пренумерандо?
3. Приведите примеры финансовых рент.
4. Как определить наращенную сумму постоянной ренты постнумерандо и сумму начисленных процентов?
5. Как определить современное значение постоянной ренты постнумерандо, ренты пренумерандо?
Специальные виды рент
