Свойства хорд и касательных

МЕТОДИЧЕСКАЯ РАЗРАБОТКА

Материалы для самоподготовки

К ЕГЭ и ГИА

по планиметрии

Часть 2

(окружности)

Автор-составитель :

СМИРНОВА

ГАЛИНА ВАСИЛЬЕВНА

АННОТАЦИЯ

Учебно-методические материалы, представленные в данном пособии, предназначаются для самоподготовки школьников и абитуриентов к ЕГЭ и ГИА по математике.

По каждой теме в пособии содержится практически весь необходимый для решения задач теоретический материал, формулы и методические рекомендации. Представлено подробное решение основных видов задач по теме , а также приведено большое количество заданий для самостоятельного решения.

Надеемся, что данное пособие поможет учащимся быстро систематизировать знания и овладеть методами решения задач по планиметрии

СОДЕРЖАНИЕ:

Занятие 8

Окружность и круг . Основные понятия и свойства.

Длина окружности и площадь круга

Углы, связанные с окружностью.

Касательная к окружности, хорды, секущие. Их свойства.

Занятие 9

Теорема синусов. Теорема косинусов.

Теорема о биссектрисе внутреннего угла треугольника

Занятие 10

Вписанные и описанные около треугольника окружности. Вневписанная окружность.

Занятие 11

Вписанные и описанные около четырехугольника окружности.

Занятие 12

Правильные многоугольники и соотношения в них.

Занятие 8

Окружность и круг . Основные понятия и свойства.

Длина окружности и площадь круга

Углы, связанные с окружностью.

Касательная к окружности, хорды, секущие. Их свойства.

Окружность и круг. Основные понятия и свойства. Длина окружности и площадь круга

Окружность — замкнутая кривая, все точки которой одинаково удалены от данной точки (центра).

Круг — часть плоскости, ограниченная окружностью.

Радиус— отрезок прямой, соединяющий центр окружности с какой-либо её точкой/

Отрезок, соединяющий две точки окружности, называется хордой.

Хорда, проходящая через центр окружности называется диаметром. Диаметр окружности равен двум радиусам.

Отношение длины окружности к её диаметру одинаково для всех окружностей. Это отношение есть трансцендентное число, обозначаемое греческой буквой пи: π=3,14159...

Длина окружности: С = 2πR

Площадь круга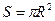

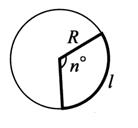
Сектором круга называется часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга.

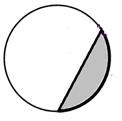
Сегментом называется часть круга, ограниченная дугой и стягивающей её хордой.

Площадь сектора равна 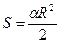, где α — угловая величина дуги в радианах, R — радиус. Длина дуги такого сектора вычисляется по формуле 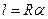. Если угол 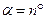, то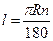

Свойства хорд и касательных

ТЕОРЕМА Диаметр, перпендикулярный к хорде, делит эту хорду и обе стягиваемые ею дуги пополам.

ТЕОРЕМА Диаметр, проведенный через середину хорды (дуги) , перпендикулярен этой хорде.

ТЕОРЕМА Дуги, заключенные между параллельными хордами, равны.

ТЕОРЕМА В одном круге ( или в равных кругах) если дуги равны, то равны и стягиваемые ими хорды и наоборот.

ТЕОРЕМА В одном круге ( или в разных кругах) равные хорды равноудалены от центра, и наоборот, если хорды равноудалены от центра , то они равны.

Прямая, имеющая с окружностью ровно одну общую точку называется касательной к окружности.

ТЕОРЕМА Если прямая касательная к окружности, то она перпендикулярна к радиусу, проведенному и точку касания.

ТЕОРЕМА Если прямая перпендикулярна радиусу, проведенному через общую точку прямой и окружности, то прямая касательная к окружности.

ТЕОРЕМА Две касательные, проведенные к окружности из одной точки, равны и образуют равные углы с прямой, соединяющей эту точку с центром окружности.

ТЕОРЕМА Если две окружности имеют общую точку, расположенную вне линии центров, то они имеют и другую общую точку, симметричную с данной относительно линии центров.

ТЕОРЕМА Общая хорда двух пересекающихся окружностей перпендикулярна к линии центров и делится ею пополам.

ТЕОРЕМА Если две окружности касаются, то точка касания лежит на линии их центров.

ТЕОРЕМА Если через точку, взятую внутри круга, проведены хорда и диаметр, то произведение отрезков хорды равно произведению отрезков диаметра.

Следствие: если через точку внутри круга проведены хорды, то произведение отрезков этих хорд есть величина постоянная.

ТЕОРЕМА Если из точки вне круга проведены к нему касательная и секущая, то квадрат касательной равен произведению секущей на ее внешнюю часть.

Следствие: если из точки вне круга проведены к нему секущие, то произведение секущей на ее внешнюю часть есть величина постоянная.