Уточнение корней методом хорд

В отличие от метода дихотомии, обращающего внимание лишь на знаки значений функции, но не на сами значения, метод хорд использует пропорциональное деление интервала. Название метода происходит из того, что конструируемые по ходу дела прямые являются хордами по отношению к графику функции.

Итак, пусть функция f(x) удовлетворяет условиям теоремы о существовании корней непрерывной функции (см. с.5) и, тем самым, найден отрезок [a,b], содержащий по крайней мере один корень. Получим формулу для двухшагового метода хорд. Вычисляем значения функции на концах отрезка, и строим "хорду", соединяющую точки А(a,f(a)) и В(b,f(b)). В методе хорд процесс итераций состоит в том, что в качестве приближения к корню уравнения (1) принимают значение x₀ точки пересечения хорды, соединяющей точки А(a,f(a)) и В(b,f(b)) c осью абсцисс. Уравнение хорды выписывается как каноническое уравнение прямой между этими точками:

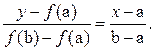( 3)

Для точки пересечения с осью абсцисс x=x₀, y=0 получим уравнение: 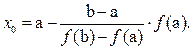Сравнивая знаки произведений f(a)×f(x₀) и f(b)×f(x₀), находим произведение, которое меньше 0, и сужаем интервал до [a,x₀] или [x₀ ,b]. Проводим соответствующие переобозначения концов отрезка. Продолжаем процесс построения хорд до тех пор, пока разница между очередными приближениями не окажется достаточно малой (в пределах допустимой погрешности)
|b-a|<e . Метод называется двухшаговым, так как для его реализации требуется не одно, а два начальных приближения (начало отрезка а и конец отрезка b).

На практике чаще применяется одношаговый метод хорд. Потребуем, чтобы функция f(x) удовлетворяла условиям следствия 3 теоремы о существовании корней непрерывной функции (см. с. 6). Также, как и выше, заменяем функцию f(x) на каждом шаге итерационного процесса поиска хордой, пересечение которой с осью абсцисс дает приближение корня x₀. При этом в процессе поиска семейство хорд можно строить:

а) при фиксированном левом конце хорд;

б) при фиксированном правом конце хорд.

Метод обеспечивает быструю сходимость, если f(x₀) × f ''(x) > 0, поэтому хорды
фиксируются на том конце интервала [a,b], где знаки функции и ее кривизны
совпадают.

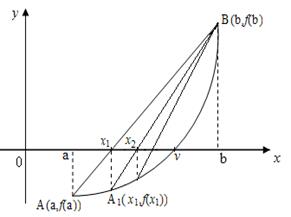
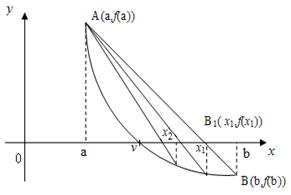
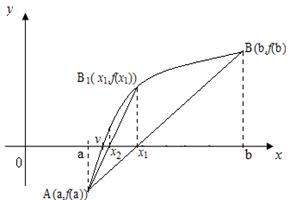
Рассмотрим случай (рис.7), когда первая и вторая производные имеют одинаковые знаки на [a,b], т.е. 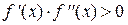, "xÎ[a,b]. Это означает, что либо f '(x) > 0 и f ''(x) > 0, то есть функция возрастает и выпукла вниз на этом отрезке (рис.7 а)), либо f '(x) < 0 и f ''(x) < 0, то есть функция убывает и выпукла вверх на этом отрезке (рис.7 б)). В этом случае граница b зафиксирована, а x₀=a. Пусть, далее, x₁ - точка пересечения хорды (3) с осью Оx. Так как y = 0, то

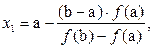
и x₁ может считаться приближенным значением корня.

a) б)

Рис. 7. Случай, когда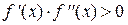

Аналогично для хорды, проходящей через точки A₁( x₁,f(x₁)) и B(b,f(b)), вычисляется следующее приближение корня:

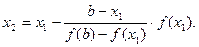
В общем случае формула метода хорд имеет вид:

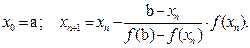( 4)

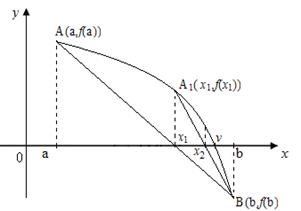
Другой случай, когда первая и вторая производные имеют разные знаки, т.е. 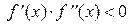,"xÎ[a,b] (рис.8). В этом случае, либо f '(x) < 0 и f ''(x) > 0, то есть функция убывает и выпукла вниз на этом отрезке (рис.8 а)), либо
f '(x) > 0 и f ''(x) < 0, то есть функция возрастает и выпукла вверх на этом отрезке (рис.8 б)). Тогда все приближения к корню x=v выполняются со стороны правой границы отрезка [a,b] (конец а неподвижен, рис.8) и вычисляются по формуле (5):

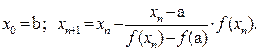( 5)

a) б)

Рис. 8. Случай, когда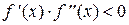

Выбор формулы в каждом конкретном случае зависит от вида функции f(x) и осуществляется по правилу: неподвижной является такая граница отрезка [a,b] изоляции корня, для которой знак функции совпадает со знаком второй производной. Формула (4) используется в том случае, когда 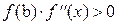. Если справедливо неравенство 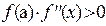, то целесообразно применять формулу (5).

Итерационный процесс метода хорд продолжается до тех пор, пока не будет получен приближенный корень x^* с заданной степенью точности e. В качестве приближенного значения корня следует взять x^*= x_n . Реализация алгоритма метода хорд представлена на блок-схеме в прил.2. При оценке погрешности приближения можно пользоваться соотношением

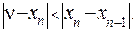
Если обозначить через m наименьшее значение |f '(x)| на промежутке [a, b], которое можно определить заранее, то получим формулу для оценки точности вычисления корня:

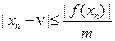или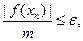

где e - заданная погрешность вычислений.