Тема 2.1.-2.2. Вычисление наращенной суммы на основе сложных дискурсивных процентов. Сравнение интенсивности процессов наращивании и дисконтирования по разным видам процентных ставок.

В финансовой практике значительная часть расчетов ведется с использованием схемы сложных процентов. Применение схемы сложных процентов целесообразно в тех случаях, когда:

− проценты не выплачиваются по мере их начисления, а присоединяются к первоначальной сумме долга. Присоединение начисленных процентов к сумме долга, которая служит базой для их начисления, называется капитализацией процентов;

− срок ссуды более года.

Если процентные деньги не выплачиваются сразу по мере их начисления, а присоединяются к первоначальной сумме долга, то долг, таким образом, увеличивается на невыплаченную сумму процентов, и последующее начисление процентов происходит на увеличенную сумму долга:

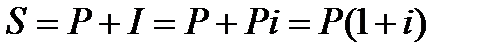– за один период начисления;

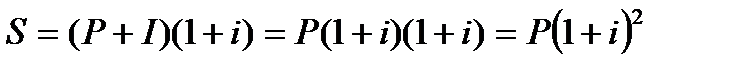– за два периода начисления;

отсюда, за n периодов начисления формула примет вид: ,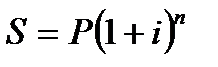

где 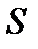– наращенная сумма долга; 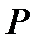– первоначальная сумма долга; i – ставка процентов в периоде начисления; n – количество периодов начисления. Эта формула называется формулой сложных процентов.

Различие начисления простых и сложных процентов в базе их начисления. Если простые проценты начисляются все время на одну и ту же первоначальную сумму долга, т.е. база начисления является постоянной величиной, то сложные проценты начисляются на увеличивающуюся с каждым периодом начисления базу.

Графическая иллюстрация соотношения наращенной суммы по простым и сложным процентам представлена на рисунке.

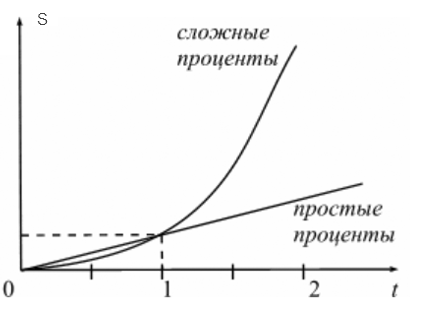Рис.1 Наращение по простым и сложным процентам

Как видно из рисунка, при краткосрочных ссудах начисление по простым процентам предпочтительнее, чем по сложным процентам; при сроке в один год разница отсутствует, но при среднесрочных и долгосрочных ссудах наращенная сумма, рассчитанная по сложным процентам значительно выше, чем по простым.

При любом i,

если 0 < n < 1, то (1 + ni) > (1 + i)ⁿ

если n > 1, то (1 + ni) < (1 + i)ⁿ

если n = 1, то (1 + ni) = (1 + i)ⁿ

Таким образом, для лиц, предоставляющих кредит:

− более выгодна схема простых процентов, если срок ссуды менее года (проценты начисляются однократно в конце года);

− более выгодной является схема сложных процентов, если срок ссуды превышает один год;

− обе схемы дают одинаковый результат при продолжительности периода один год и однократном начислении процентов.

Достаточно часто финансовые контракты заключаются на период, отличающийся от целого числа лет.

В случае, когда срок финансовой операции выражен дробным числом лет, начисление процентов возможно с использованием двух методов:

− общий метод заключается в прямом расчете по формуле сложных процентов:

, ,

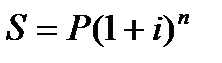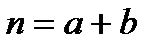где n – период сделки; a – целое число лет; b – дробная часть года.

− смешанныйметод расчета предполагает для целого числа лет периода начисления процентов использовать формулу сложных процентов, а для дробной части года – формулу простых процентов:

.

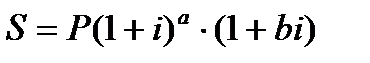Поскольку b < 1, то (1 + bi) > (1 + i)^a, следовательно, наращенная сумма будет больше при использовании смешанной схемы.

Cмешанная схема более выгодна кредитору.