Формирование оптимального портфеля ценных бумаг

На финансовом рынке обращается множество ценных бумаг: государственные ценные бумаги, муниципальные облигации, корпоративные акции и т.д. Если у участника рынка есть свободные деньги, то их можно отнести в банк и получать проценты или купить на них ценные бумаги и получать дополнительный доход. Но в какой банк отнести? Какие ценные бумаги купить? Малорисковые ценные бумаги, как правило, и малодоходны, высокодоходные, как правило, более рисковые. Экономическая наука может дать некоторые рекомендации для решения этого вопроса

Рассмотрим общую задачу распределения капитала, который участник рынка хочет потратить на покупку ценных бумаг, по различным видам ценных бумаг. Предваряя точные математические постановки, констатируем очевидную общую цель инвестора – вложить деньги так, чтобы сохранить свой капитал, а при возможности и нарастить его.

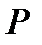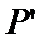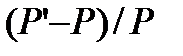Набор ценных бумаг, находящихся у участника рынка, называется его портфелем. Стоимость портфеля – это суммарная стоимость всех составляющих его бумаг. Если сегодня его стоимость есть , а через год она окажется равной , то естественно назвать доходностью портфеля в процентах годовых. Т.е. доходность портфеля – это доходность на единицу его стоимости.

Пусть 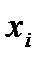– доля капитала, потраченная на покупку ценных бумаг 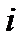-го вида. Рассуждения о долях эквивалентны тому, что весь выделенный капитал принимается за единицу. Пусть 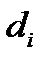– доходность в процентах годовых ценных бумаг 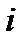-го вида в расчете на одну денежную единицу.

Найдем доходность всего портфеля 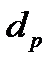. С одной стороны, через год капитал портфеля будет равен 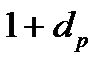, с другой - стоимость бумаг 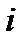-го вида увеличиться с 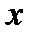до 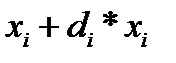, так что суммарная стоимость портфеля будет равна 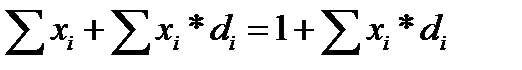. Приравнивая оба выражения для стоимости портфеля, получаем .

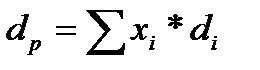Итак, задача увеличения капитала портфеля эквивалентна аналогичной задаче о доходности портфеля, выраженной через доходности бумаг и их доли.

Как правило, доходность бумаг колеблется во времени, так что будем считать ее случайной величиной. Пусть 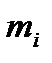, 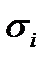– средняя ожидаемая доходность и среднее квадратическое отклонение (СКО) этой случайной доходности, т.е. 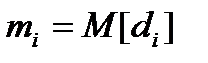- математическое ожидание доходности и 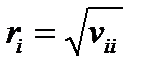, где 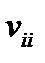– вариация или дисперсия 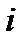-ой доходности. Будем называть 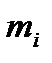, 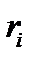соответственно эффективностью и риском 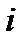-ой ценной бумаги. Через 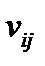обозначим ковариацию доходностей ценных бумаг 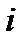-го и 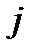-го вида (или корреляционный момент ).

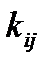Так как доходность составляющих портфель ценных бумаг случайна, то и доходность портфеля есть также случайная величина. Математическое ожидание доходности портфеля есть 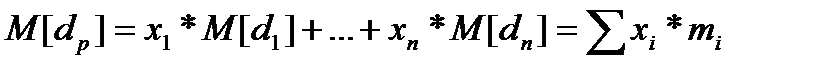обозначим его через 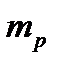. Дисперсия доходности портфеля есть 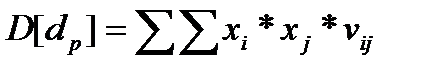. Так же, как и для ценных бумаг, назовем 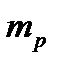эффективностью портфеля, а величину 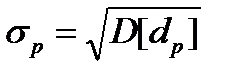– риском портфеля 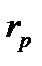. Обычно дисперсия доходности портфеля называется его вариацией .

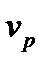Итак, эффективность и риск портфеля выражены через эффективности составляющих его ценных бумаг и их совместные ковариации.

Портфель Марковица минимального риска. Существует несколько вариантов задач оптимизации рискового портфеля. Мы рассмотрим только одну. Это так называемый «портфель Марковица». Эта задача была сформулирована и решена американским экономистом Г. Марковицем (H. Markovitz) в 1952 году , за что позднее он получил нобелевскую премию.

Пусть имеются 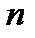видов ценных бумаг, из которых инвестор хочет сформировать портфель. Необходимо найти 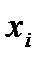, минимизирующие вариацию портфеля

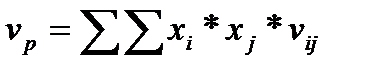(3.4.1)

при условии, что обеспечивается заданное значение эффективности портфеля ,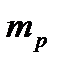

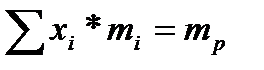. (3.4.2)

Поскольку 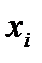– доли, то в сумме они должны составлять единицу:

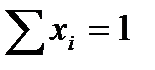. (3.4.3)

Оставив за инвестором выбор средней эффективности портфеля и помогая ему минимизировать в этом случае неопределенность, получаем следующую задачу по оптимизации портфеля ценных бумаг:

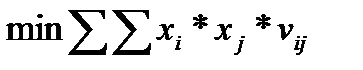
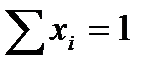(3.4.4)

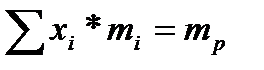
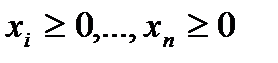
Это задача квадратичного программирования. Опустив условия неотрицательности переменных, получаем собственно задачу Марковица.

Решение.

С помощью функции Лагранжа сведем задачу на условный экстремум к задаче на безусловный экстремум:

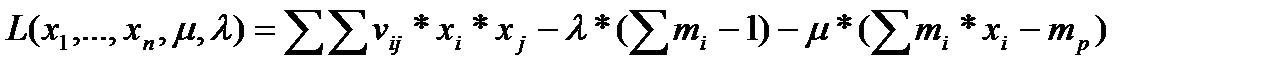(3.4.5),

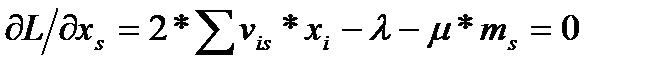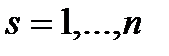, . (3.4.6)

производные по 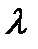, 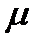воспроизводят указанные выше два соотношения, тем самым для 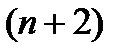переменных 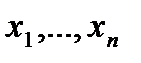, , 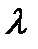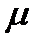получаем 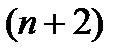уравнения.

Запишем полученные уравнения в матричной форме, используя следующие обозначения:

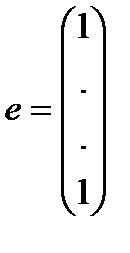
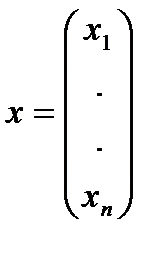
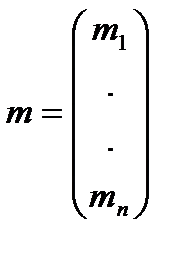
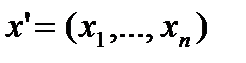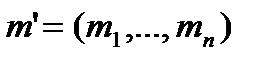, (3.4.7)

Штрих применяется для обозначения операции транспонирования матрицы.

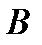- матрица ковариаций, 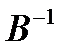– обратная ей матрица. Следовательно уравнения (3.4.6) примут вид:

,

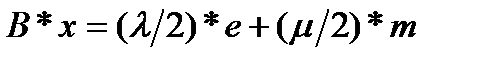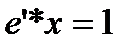, (3.4.8)

.

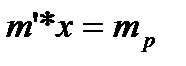Основное допущение этой модели состоит в том, что между эффективностями 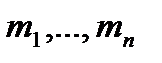нет линейной связи, поэтому ковариационная матрица 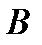невырождена 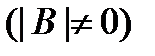, следовательно, существует обратная матрица 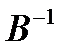. Используя этот факт разрешим в матричной форме относительно :

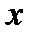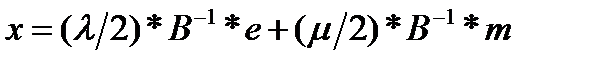, (3.4.9)

подставив это решение в первое и второе условия, получим два уравнения для определения 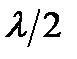и :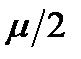

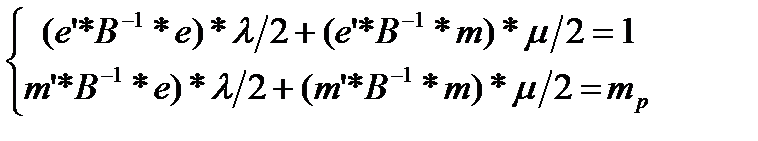(3.4.10)

Решая два последних уравнения по правилу Крамера, находим

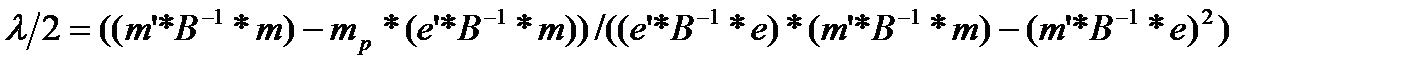(3.4.11)

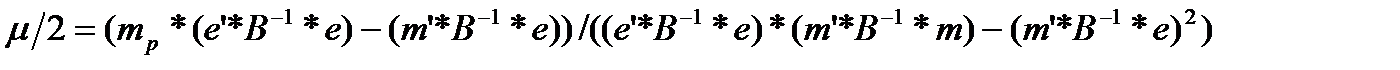
Подставляя это решение в (3.4.9) получаем следующую структуру оптимального портфеля:

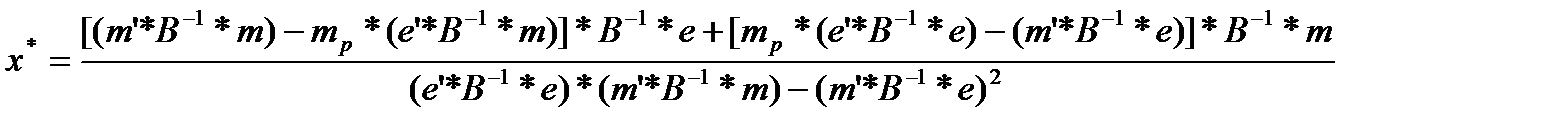(3.4.12)

Простой подстановкой убеждаемся, что 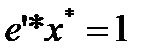и .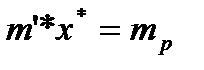

Кроме того, находим минимальную дисперсию, соответствующую оптимальной структуре:

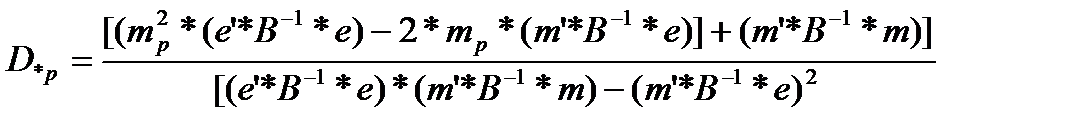(3.4.13)

Тогда 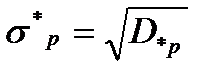, что и является минимальным риском портфеля.

Если 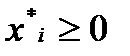, то это означает рекомендацию вложить долю 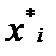наличного капитала в ценные бумаги 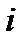-го вида. Если же 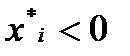, то содержательно это означает провести операцию “short sale” (“короткая продажа”).

Что это за операция? Инвестор, формирующий портфель, обязуется через какое-то время поставить ценные бумаги 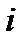-го вида (вместе с доходом, какой они принесли бы их владельцу за это время). За это сейчас он получает их денежный эквивалент. Эти деньги он присоединяет к своему капиталу и покупает рекомендуемые оптимальным решением ценные бумаги. Так как ценные бумаги других видов (т.е. не 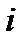-го вида) более эффективны, то инвестор оказывается в выигрыше.

Математически эта операция значит, что нужно исключить этот вид ценных бумаг из рассмотрения и решить задачу заново.

Пример.

Дано: 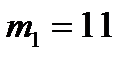, , 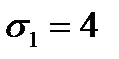, , 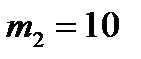, , 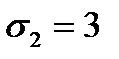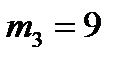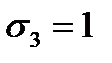ценные бумаги не коррелированы. Определить оптимальный портфель при .

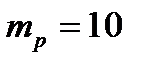Ответ: Доли ценных бумаг: 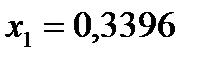; ; 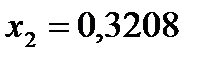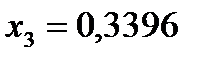. Минимальный риск 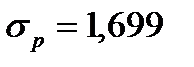. Эффект диверсификации портфеля наглядно виден на данном примере. Портфель имеет такую же эффективность, как если бы он был составлен только из бумаг 2-го вида, но его риск значительно меньше, чем у бумаг 2-го вида ( ).

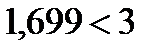В Приложении 1 приведен листинг программы, которая рассчитывает структуру портфеля ценных бумаг при заданной эффективности и его минимальный риск. В Приложениях 2-5 наглядно представлен интерфейс программы.

В качестве экспериментального представления задачи в данной работе представлен расчет доходности акций ОАО «Газпром». Расчет произведен в файле Microsoft Excel.

В Приложении 6 и приложении 7 представлены графики изменения цены и доходности акций ОАО «Газпром» за период с 11.04.2011 по 11.04.2012.

Заключение

Широкое внедрение электронно-вычислительной техники во все сферы нашей жизни в последнее время, вызвало бурный рост технологий, связанных с применением в них средств вычислительной техники. Одной из наиболее крупных отраслей развития технологий с применением ЭВМ, является математическое моделирование, которое достаточно просто (в отличие от аналогового моделирования) может быть реализовано на ЭВМ разных модификаций и возможностей. Связано это с тем, что при математическом моделировании модель представляет собой определенную последовательность математических зависимостей и динамика такой модели представляет собой изменение параметров зависимостей в результате выполнения расчетов. Математическое моделирование тесно связано с имитационным моделированием. Одним из разделов математического моделирования, являются модели систем массового обслуживания и их изучение.

В данной дипломной работе были рассмотрены методы прикладной математике, применяемые в моделировании банковской деятельности. Большинство распространенных математических технологий тем или иным образом воплощены в информационных технологиях.

Информационные системы являются комплексом моделей предметной области (реального или виртуального мира). Информационные системы могут включать в себя в качестве компонент (подмоделей) как базы данных, так и математические, логические, имитационные модели объектов и/или процессов.

Кроме того, широко распространены программные продукты (пакеты прикладных программ), поддерживающие (и поддерживаемые) определенные информационно-математические технологии. Например, модели системной динамики (глобального моделирования), программы статистической обработки и регрессионного анализа (построения статистических моделей), программные средства экономико-математического моделирования, информационно-поисковые и информационно-логические системы и пр.

По всей видимости, серьезные исследования исторических, демографических, экологических, экономических и пр. процессов невозможны без использования в качестве информационного и математического обеспечения баз данных и пакетов прикладных программ.

В дипломном проекте мною были рассмотрены и решены многие задачи математического моделирования банковской деятельности, поставленные в начале работы. Произведено исследование методов экономико-математического моделирования в прогнозировании деятельности кредитной организации. Обобщая проведенную работу, считаю, основные проблемы в сфере банковского дела и связанного с ним математического моделирования рассмотрены в полной мере, методы рассмотрены в полном объеме.

Также была реализована программа, которая формирует оптимальный портфель ценных бумаг по заданным параметрам. Для написания программы был использован язык программирования Visual Basic for Applications.

Список использованной литературы

1. Амелин И.Э.,Царьков В.А. «План-матрица развития Банка», журнал «Банки и технологии», РЕГ. №012846, №1 2002. – 49 с.

2. Андреев М.Ю., Пильник Н.П., Поспелов И.Г.Эконометрическое исследование и модельное описание деятельности современной российской банковской системы. М., ВЦ РАН,2008. – 171 с.

3. Базара М., Шетти К. Нелинейное программирование. Теория и алгоритмы М.: Мир, 1982. – 583 с.

4. Банди Б. Основы линейного программирования: Пер. с англ. – М.: Радио и связь, 1989.- 176 с.: ил

5. Беляков А.В. Банковские риски. Проблемы учета, управления и регулирования. - М.: БДЦ-Пресс, 2003. – 305 с.

6. Джон Уокенбах. Профессиональное программирование на VBA в Excel 2002: Пер. с англ.-М.: Издательский дом «Вильямс», 2004 .-784 с.

7. Дяченко О. Рейтинг банковских рисков: Что пугает банкиров\\ Банковское обозрение, №1, 2005. –203 с.

8. Егорова Н. Е., Смулов А.М., Математические методы финансового анализа банковской деятельности. Аудит и финансовый анализ. Международной конференции, посвященной 90-летию Л. С. Понтрягина – М.: МГУ, сентябрь 1998. – 208 с.

9. Егорова Н.Е., Смулов А.С.Предприятия и банки: взаимодействие, экономический анализ и моделирование.-М.;Дело,2002. –457 с.

10. Жуков Е.Ф. Банки и банковские операции: Учебник для вузов. М.: Банки и биржи, ЮНИТИ ,1997 . – 471 с.

11. Иода Е.В., Мешкова Л.Л., Болотина Е.Н. Классификация банковских рисков и их оптимизация. – Тамбов, 2002. –432 с.

12. Канаев А.В.Стратегическое управление коммерческим банком. Концептуальные основы. Монография.СПбГУ,2006. –221 с.

13. Кинг М. Политика независимости центрального банка. Central Banking, №3, 2001. – 150 с. (перевод СИЦ Банка России).

14. Колесников В. И., Кроливецкая Л. П. «Банковское дело», М.: Финансы и статистика, 2006 . – 428 с.

15. Конюховский П. В. Микроэкономическое моделирование банковской деятельности. – СПб: Питер, 2001. –224 с.: ил. – (Серия «Ключевые вопросы»).

16. Кристиан Олбрайт. Моделирование с помощью Microsoft Excel и VBA: разработка систем принятия решений.: Пер. с англ.- Издательский дом «Вильямс», 2005 . –672 с.

17. Кузнецов А. В. И др. Высшая математика: Математическое программирование.: Учеб./А.В. Кузнецов, В. А. Сакович, Н. И. Холод; Под общ. ред. А. В. Кузнецова. – Мн.: Выш. шк., 2001. –286 с.: ил.

18. Ластра Р. Центральные банки между подотчетностью и независимостью. Central Banking, 2001. –234 с. (перевод СИЦ Банка России).

19. Малюгин В. Оценка устойчивости банков на основе эконометрических моделей. Малюгин В., Пытляк Е. // Банковской вестник. – 2007. – №1. – 36 с.

20. Масленников В.В. Зарубежные банковские системы. Иваново: Талка, 2007. – 360 с.

21. Мещеряков Г.Ю. Общебанковская система риск-менеджмента // Вестник АРБ, №15, 2009. –342 с.

22. Ольхова Р.Г.Банковское дело. Управление в современном банке. Учебное пособие. М.,КноРус,2008. –252 с.

23. Партыка Т. Л., Попов И. И. Математические методы: учебник. 2-е изд., испр. И доп. – М.: ФОРУМ: ИНФРА-М, 2007. – 464 с.: ил.

24. Первозванский А.А Финансовый рынок: расчет и риск. – М., 2009. –320 с.

25. Поляков В.П., Московкина Л.А. Структура и функции центральных банков. Зарубежный опыт. М., ИНФРА-М, 1996. – 427 с.

26. Смирнов С.Н. Риски рыночной ликвидности: измерение и управление, Международная конференция «Международный опыт риск-менеджмента и особенности развивающихся рынков», М., 2004. – 543 с.

27. Смит Вера. Происхождение центральных банков. Институт национальной модели экономики. 1990. – 724 с.

28. Тосунян Г.А. Конституционная экономика и статус Центрального банка. М., ММВБ. 2001. – 462 с.

29. Туркин О.В. VBA. Практическое программирование. М.: САЛОН-ПРЕСС, 2007. –128с.

30. Хелферт Э. Техника финансового анализа. М.: Аудит: ЮНИТИ, 2007. –123 с.

31. Центральные банки и банковские системы. ЦПП Банка России. М., 2000. – 433 с.

32. Центральный банк в условиях рыночной экономики: мировой и российский опыт. (По материалам заседания за круглым столом, проведенного в Финансовой академии при Правительстве Российской Федерации в апреле 2002г.). Деньги и кредит, 31.07.2002. – 233 с.

33. Шапкин А.С., Шапкин В.А. – Теория риска и моделирование рисковых ситуаций – М: Дашков и К, 2007. –620 с.

34. Шарп У., Александер Г., Бэйли Дж. Инвестиции: Пер. с англ. - М.: ИНФРА-М, 2008. – 1028 с.

35. Шелобаев С. И. Математические методы и модели в экономике, финансах, бизнесе: Учеб. Пособие для вузов. – М.: ЮНИТИ-ДАНА, 2001. – 367с.

36. Шоломицкий, А.Г. Теория риска. Выбор при неопределенности и моделирование риска. – М.: Изд. дом ГУ ВШЭ, 2005. –450 с.

37. Baltensperger, Ernst Alternative Approaches to the Theory of the Banking Firm / Baltensperger, Ernst // Journal of Monetary Economics. – 1980. – №1 – Р. 37.

38. Murphy, Neil B. Costs of Banking Activities: Interactions Between Risk and Operating Costs: A comment Murphy, Neil B. // Journal of Money, Credit and Banking. – 2009. – August. – Р. 722.

Приложения

Приложение 1

Листинг программы

'объявление переменных

Dim n%, st$ 'количество и строка для вывода

Dim t As Object 'объекты для просматривания текстбоксов

Dim t1(10) As Object '

Dim t2(10) As Object

Dim t3(9, 10) As Object

Dim Cont As Control 'контрол , для просмотра контролов на форме

'====

Dim a! 'переменные для расчетов

Dim m!(), be!(), Bm!()

Dim b(), E(), B1(), E1()

Dim i%, k%, c%, v%, l%, j%

Dim mp!, ebe!, mbm!, ebm!, X!, mbe!

Dim u As Boolean 'логическая переменная - индикатор корректности ввода

'процедура общая для расчетов

Sub riski()

ReDim m!(10), be!(10), Bm!(10) 'объявления массивов

ReDim b(10, 10), E(10, 10), B1(10, 10), E1(10, 10)

'обнуление переменных (необходимо после предыдущего расчета)

mp = 0: ebe = 0: mbm = 0: ebm = 0: X = 0: mbe = 0

c = 0: v = 0: l = 0

Продолжение приложения 1

'вызов процедуры

Call vvod 'ввода

If Not (u) Then 'если ввод корректен , то

Call base 'базовую или расчетную

Call vivod 'вывод

End If

End Sub

Sub base() ' процедура базовую или расчетную

For i = 1 To n 'обращение матрицы B

For c = 1 To n

For v = 1 To n

B1(c, v) = b(c, v)

E1(c, v) = E(c, v) 'дублирование матриц

Next

Next

For k = 1 To n

b(i, k) = B1(i, k) / B1(i, i) 'деление строки на разрешающий элемент

E(i, k) = E1(i, k) / B1(i, i)

For l = 1 To n

'нахождение остальных элементов

If l <> i Then

Продолжение приложения 1

b(l, k) = (B1(l, k) - (B1(l, i) * B1(i, k) / B1(i, i)))

E(l, k) = (E1(l, k) - (B1(l, i) * E1(i, k) / B1(i, i)))

End If

Next

Next

Next

For i = 1 To n 'суммирование по строкам, формирование вектора-столбца Be

For j = 1 To n

be(i) = be(i) + E(i, j)

Next

Next

For i = 1 To n 'формирование вектора-столбца Bm

For j = 1 To n

Bm(i) = Bm(i) + m(j) * E(i, j)

Next

Next

For i = 1 To n 'нахождение констант

ebe = ebe + be(i) 'суммирование по стоблцу

ebm = ebm + Bm(i)

mbm = mbm + m(i) * Bm(i)

mbe = mbe + m(i) * be(i)

Продолжение приложения 1

Next

End Sub

Sub vvod() 'ввод

Dim z!, mi!, ma!

u = True 'для начала индикатор корректности ставится в состояние ДА

For i = 1 To n 'в цикле по размеру матрицы (количество док)

E(i, i) = 1 'заполняем диагональ единицами

m(i) = Val(t1(i).Text) 'считывание эффективности

If (m(i) < 0) Then 'если полученно отрицательное значение, то выводится сообщение об этом

MsgBox " Ошибка ввода! Величина эффективности должна быть положительной! ", vbExclamation

Exit Sub 'выход из процедуры

End If

Next

For i = 1 To n ' так же для рисков

z = Val(t2(i).Text)

If (z < 0) Then

Продолжение приложения 1

MsgBox " Ошибка ввода! Величина риска должна быть положительной! ", vbExclamation

Exit Sub

End If

'в случае корректного ввода сразу возводиться считанное в квадрат

b(i, i) = z * z

Next

For i = 1 To n 'так же

For j = i + 1 To n 'ввод матрицы ковариации

z = Val(t3(i, j).Text)

'если выполнено условие ниже , то выводиться сообщение

If Abs(z) >= Sqr(b(i, i)) * Sqr(b(j, j)) Then

MsgBox " Ошибка ввода! Корреляционный момент должен быть положительным и меньше произведения СКО этих бумаг! ", vbExclamation

Exit Sub 'завершение процедуру

End If

'в случае корректного воода

b(i, j) = z ' симметрирование матрицы

b(j, i) = z

If i <> j Then

E(i, j) = 0 'записывание нулей в массив Е не на главной диагонали

End If

Next

Продолжение приложения 1

Next

'определение максимума

ma = 0 'для начала 0

For i = 1 To n 'если находим больше - то его и принимаем за максимум

If m(i) > ma Then ma = m(i)

Next

'определение минимума

mi = 100000000 'для начала 10000000 (как чрезмерно большое значение)

For i = 1 To n

If m(i) < mi Then mi = m(i) 'если находим меньше - то его и принимаем за минимум

Next

mp = Val(t.Text) 'считывание желаемой эффективности

If (mp < mi) Or (mp > ma) Then 'если или одно, или другое условие выполнено

MsgBox " Ошибка ввода!" & vbLf & _

" Желаемая эффективность должна быть в пределах эффективностей ценных бумаг!: ", vbExclamation

Exit Sub

End If

'если к этому моменту не было выхода из процедуры,

'то ввод корректен

Продолжение приложения 1

u = False

End Sub

Sub vivod() 'вывод

ReDim mass_diagramm(10)

ind_m = 0

ks = 0 'контрольная сумма для начала 0

On Error Resume Next 'в случае возникновения непредвиденной ошибки продолжаем работу

'заголовок

st = " Структура портфеля." & vbLf & vbLf & " Доли ценных бумаг."

For i = 1 To n 'в цикле по количеству бумаг

'вычисление по соответствующим формулам долей

X = ((mbm - mp * ebm) * be(i) + (mp * ebe - mbe) * Bm(i)) / (ebe * mbm - mbe * mbe)

ind_m = ind_m + 1

mass_diagramm(ind_m) = X

'и дописывание к строке для вывода с округлением до 7 знака

st = st & vbLf & i & "-го вида " & Round(X, 7)

ks = ks + X 'накапливание контрольной суммы

If X < 0 Then 'если доля меньше 0

'записывание в строку для вывода

st = st & vbLf & vbLf & " Так как доля бумаг " & i & "-го вида отрицательна, то необходимо"

Продолжение приложения 1

st = st & vbLf & " провести сделку 'short sale', исключить бумаги этого вида из портфеля"

st = st & vbLf & " и решить задачу заново."

End If

Next

'дописывание в строку для вывода через две строчки вычисляемый риск

st = st & vbLf & vbLf & " Минимальный риск портфеля: " & Round(Sqr((mp * mp * ebe - 2 * mp * mbe + mbm) / (ebe * mbm - mbe * mbe)), 7)

'вывод сформированной строки и контрольной суммы с округлением последней до 1 знака

MsgBox st & vbLf & "kontrol summ = " & Round(ks, 1)

If Err.Number > 0 Then 'если возникла непредвиденная ошибка --- ее номер больше 0

MsgBox "Допущены ошибки ввода /некорректные данные/" 'то выводится сообщение об этом

End If

End Sub

Private Sub ComboBox1_KeyPress(ByVal KeyAscii As MSForms.ReturnInteger)

KeyAscii = 0 'нажатие на комбобокс возвращает код клавиши 0

'тем самым запрет на ввод данных, а только выбор

End Sub

Продолжение приложения 1

Private Sub ComboBox2_Change()

End Sub

Private Sub ComboBox2_Click()

MSChart1.ChartType = ComboBox2.ListIndex

End Sub

Private Sub CommandButton1_Click()

For i = 1 To n 'в цикле по количеству типов бумаг

'если поле пустое или не число

If t1(i).Text = "" Or Not (IsNumeric(t1(i).Text)) Or _

t2(i).Text = "" Or Not (IsNumeric(t2(i).Text)) Or _

t.Text = "" Or Not (IsNumeric(t.Text)) Then 'то выводится сообщение и выход

MsgBox "Не заполнены все поля или введено нечисловое значение", vbExclamation

Exit Sub

End If

Next i

For i = 1 To n - 1 'также для полей матрицы

Продолжение приложения 1

For j = i + 1 To n

If t3(i, j).Text = "" Or Not (IsNumeric(t3(i, j).Text)) Then

MsgBox "Не заполнены все поля или введено нечисловое значение", vbExclamation

Exit Sub

End If

Next j

Next i

'если к этому моменту не было выхода из процедуры - значит все верно

U_Activate 'вызов процедуры стартовой активации

Call riski 'и общей процедуры расчета

Call Diagramm

End Sub

Private Sub CommandButton2_Click() 'тест

ComboBox1.ListIndex = 1 'устанавление тестовых входных данных

n = 3

TextBox1.Text = 11: TextBox2.Text = 10: TextBox3.Text = 9

TextBox111.Text = 4: TextBox112.Text = 3: TextBox113.Text = 1

TextBox12.Text = 0: TextBox13.Text = 0: TextBox23.Text = 0

TextBox121.Text = 10

End Sub

Продолжение приложения 1

Private Sub CommandButton3_Click() 'вывод результата на лист

Range("A:A").Clear 'чистка первого столбца

mst = Split(st, vbLf) 'образование массива из строки вывода с разделителем

' vbLf - переход на новую строку

'т.е.получение массива строк вывода

For i = 1 To UBound(mst) 'в цикле от 1 до верхней границы массва (последней строки)

Cells(i, 1) = mst(i) 'последовательно по строкам листа вывод

Next

End Sub

Private Sub Image1_Click()

Frame4.Visible = False

End Sub

Private Sub Diagramm()

'mass_diagramm (ind_m)

With MSChart1

.ColumnCount = 1

.RowCount = ind_m

For i = 1 To ind_m

Продолжение приложения 1

.Column = 1

.Row = i

.Data = mass_diagramm(i)

.RowLabel = "x" & i

Next

End With

MSChart1.Title.Text = "Гистограмма оптимального потрфеля ценных бумаг"

'MSChart1.Title.VtFont.Size = 10

'Call MSChart1.Title.VtFont.VtColor.Set(0, 128, 255)

MSChart1.Plot.Axis(VtChAxisIdX).AxisTitle = "Шкала ценных бумаг"

MSChart1.Plot.Axis(VtChAxisIdY).AxisTitle = "Шкала доль"

End Sub

Private Sub CommandButton4_Click()

UserForm3.Show

End Sub

'процедуры нажатия на надписи

' в результате выводятся соответствующие пояснения внизу формы

Продолжение приложения 1

Private Sub Label18_Click()

Label7.Caption = "Совместная вариацию (корреляционный момент) ценных бумаг." & vbLf & _

"Она не должна быть больше произведения СКО этих бумаг."

End Sub

Private Sub Label2_Click()

Label7.Caption = "количество видов ценных бумаг, из которых вы хотите " & vbLf & _

"сформировать портфель (не более 10)"

End Sub

Private Sub Label21_Click()

Label7.Caption = "При вводе рисков и совместных вариаций ценных бумаг следует " & _

" быть внимательным, так как программа не расчитана на линейную" & _

" связь доходностей ценных бумаг. Поэтому рекомендуется не вводить" & _

" пропорциональные риски и совместные вариации ценных бумаг"

End Sub

Private Sub Label3_Click()

Продолжение приложения 1

Label7.Caption = "Эффективности (доходности) ценных бумаг "

End Sub

Private Sub Label4_Click()

Label7.Caption = "Желаемая эффективность портфеля " & vbLf & _

"Она должна быть в пределах эффективностей ценных бумаг"

End Sub

Private Sub Label6_Click()

Label7.Caption = "риск (среднее квадратическое отклонение(СКО))"

End Sub

Private Sub OptionButton1_Click()

MSChart1.Chart3d

End Sub

'если движение мышки не на надписях , а на форме - то пояснения убираются

Private Sub UserForm_MouseMove(ByVal Button As Integer, ByVal Shift As Integer, ByVal X As Single, ByVal Y As Single)

If Label7.Caption <> "" Then Label7.Caption = ""

End Sub

Продолжение приложения 1

'==========================================

Private Sub ComboBox1_Click() 'выбор количества типов бумаг

n = ComboBox1.Value 'запоминание этого количества

'и устанавление области видимости матрицы

Frame1.Width = TextBox2.Left + (n - 1) * (TextBox2.Left - TextBox1.Left)

Frame1.Height = TextBox12.Top + Frame2.Top + (n - 1) * (TextBox23.Top - TextBox12.Top)

End Sub

Private Sub UserForm_Activate() 'при активации формы

For i = 2 To 10

UserForm2.ComboBox1.AddItem i 'заполнение количества для выбора

Next i

UserForm2.ComboBox1.ListIndex = 1 'и показывает 3 (так как начало отсчета 2)

U_Activate 'проводится стартовая активация (ниже)

CommandButton2_Click 'заполнение для наглядности тестовыми данными

ComboBox2.Clear

ComboBox2.AddItem "3DBar"

ComboBox2.AddItem "2DBar"

ComboBox2.AddItem "3DLine"

ComboBox2.AddItem "2DLine"

ComboBox2.AddItem "3DArea"

ComboBox2.AddItem "2DArea"

Продолжение приложения 1

ComboBox2.AddItem "3DStep"

ComboBox2.AddItem "2DStep"

ComboBox2.AddItem "3DCombination"

ComboBox2.AddItem "3DCombination"

ComboBox2.ListIndex = 1

End Sub

Private Sub U_Activate() 'стартовая активация

On Error GoTo Err 'если ошибка то на метку Err

For Each Cont In Me.Controls 'просматривание всех контролов на форме

'если первые 7 символов = "TextBox", то

If Mid(Cont.Name, 1, 7) = "TextBox" Then

i = Val(Mid(Cont.Name, 8)) 'выделение его номера

If i < 11 Then 'и раскидывание значения их

'по массивах в зависимости от номера

Set t1(i) = Cont

Else

If i > 110 And i < 121 Then

Set t2(i - 110) = Cont

Else

If i = 121 Then

Set t = Cont

Else

Продолжение приложения 1

i = Val(Mid(Cont.Name, 8, 1))

j = Val(Mid(Cont.Name, 9))

Set t3(i, j) = Cont

End If

End If

End If

End If

Next

Err: Err.Clear 'затирание номера ошибки, если она случилась (это в случае нераспознаваемого контрола)

Resume Next 'и продолжение далее

End Sub

Приложение 2