Классификация точек разрыва
Непрерывность функции в точке
Пусть функция f(x) определена в некоторой окрестности O(x0) точки x0 (включая саму точку x0).
Функция f(x) называется непрерывной в точке x0, если существует limx → x0 f(x) , равный значению функции f(x) в этой точке:
f(x) = f(x0), | (1) |
т.е.
| " O( f(x0) ) $ O(x0) : x Î O(x0) Þ f(x) Î O( f(x0) ) . |
Замечание. Равенство (1) можно записать в виде:
f(x) = f (
x ), |
т.е. под знаком непрерывной функции можно переходить к пределу.
Пусть Δx = x − x0 — приращение аргумента, Δy = f(x) − f(x0 ) — соответствующее приращение функции.
Необходимое и достаточное условие непрерывности функции в точке
Функция y = f(x) непрерывна в точке х0 тогда и только тогда, когда
Δy = 0. | (2) |
Замечание. Условие (2) можно трактовать как второе определение непрерывности функции в точке. Оба определения эквивалентны.
Пусть функция f(x) определена в полуинтервале [x0, x0 + δ ).
Функция f(x) называется непрерывной справа в точке x0, если существует односторонний предел
f(x) = f(x0). |
Пусть функция f(x) определена в полуинтервале (x0 − δ, x0].
Функция f(x) называется непрерывной слева в точке x0, если существует односторонний предел
f(x) = f(x0). |
Непрерывность суммы, произведения и частного двух непрерывных функций
Теорема 1. Если функции f(x) и g(x) непрерывны в точке х0, то в этой точке непрерывны
f(x) ± g(x), f(x) · g(x),
(g(x0) ≠ 0). |
Непрерывность сложной функции
Теорема 2. Если функция u(x) непрерывна в точке х0, а функция f(u) непрерывна в соответствующей точке u0 = f(x0), то сложная функция f(u(x))непрерывна в точке х0.
Все элементарные функции непрерывны в каждой точке их областей определения.
Локальные свойства непрерывных функций
Теорема 3(ограниченность непрерывной функции). Если функция f(x) непрерывна в точке x0, то существует окрестность O(x0), в которой f(x)ограничена.
Доказательство следует из утверждения об ограниченности функции, имеющей предел.
Теорема 4 (устойчивость знака непрерывной функции). Если функция f(x) непрерывна в точке x0 и f(x0) ≠ 0, то существует окрестность точки x0, в которой f(x) ≠ 0, причем знак f(x) в этой окрестности совпадает со знаком f(x0).
Классификация точек разрыва
Условие (1) непрерывности функции f(x) в точке x0 равносильно условию
| f(x0 − 0) = f(x0 + 0) = f(x0), | (3) |
где f(x 0 − 0) =
| lim |
| x → x0 − 0 |
f(x) и f(x0 + 0) =
| lim |
| x → x0 + 0 |
f(x) — односторонние пределы функции f(x) в точке x0.
При нарушении условия (3) точка x0 называется точкой разрыва функции f(x). В зависимости от вида нарушения условия (3) точки разрыва имеют различный характер и классифицируются следующим образом:
1. Если в точке x0 существуют односторонние пределы f(x0 − 0), f (x0 + 0) и
| f(x0 − 0) = f(x0 + 0) ≠ f(x0), |
то точка х0 называется точкой устранимого разрыва функции f(x) (рис. 1).
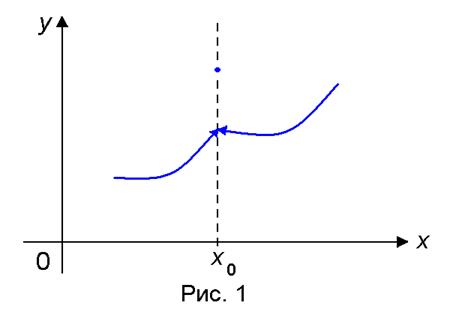
Замечание. В точке x0 функция может быть не определена.
2. Если в точке x0 существуют односторонние пределы f(x0 − 0), f (x0 + 0) и
| f(x0 − 0) ≠ f(x0 + 0), |
то точка x0 называется точкой разрыва с конечным скачком функции f(x) (рис.2).
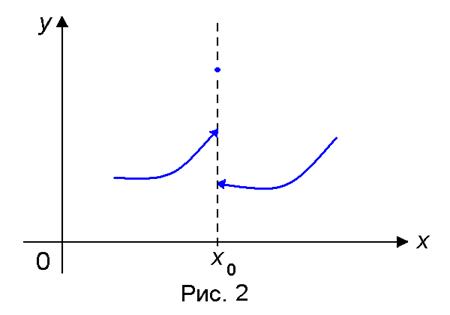
Замечание. В точке разрыва с конечным скачком значение функции может быть любым, а может быть и не определено.
Точки устранимого разрыва и конечного скачка называются точками разрыва 1–го рода. Их отличительным признаком является существование конечных односторонних пределов f(x0 − 0) и
f(x0 + 0).
3. Если в точке x0 хотя бы один из односторонних пределов f(x0 − 0), f (x0 + 0) равен бесконечности или не существует, то x0 называется точкой разрыва 2–го рода (рис. 3).
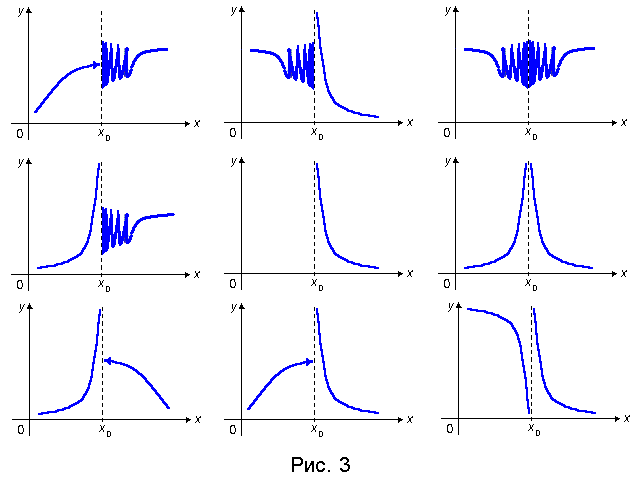
Если хотя бы один из односторонних пределов f(x0 − 0), f (x0 + 0) равен бесконечности, то прямая x = x 0 называется вертикальной асимптотой графика функции y = f(x).
