Тема 7. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ И ЕГО ПРИМЕНЕНИЕ ДЛЯ ВЫЧИСЛЕНИЯ ПЛОЩАДЕЙ ПЛОСКИХ ФИГУР
Изучение темы следует начинать с задач, приводящих к понятию определенного интеграла. Усвоить определение и свойства определенного интеграла, формулу Ньютона–Лейбница и ее применение. Изучить методы вычисления определенного интеграла и их специфику по сравнению с аналогичными методами в неопределенном интеграле, обратить внимание на применение определенного интеграла в геометрии и при решении конкретных практических задач.
Вопросы для изучения и самопроверки
1. Задачи, приводящие к понятию определенного интеграла.
2. Определенный интеграл и его свойства.
3. Формула Ньютона–Лейбница.
4. Методы вычисления определенного интеграла.
5. Применение определенного интеграла для вычисления площадей и объемов.
6. Применение определенного интеграла в задачах практического характера.
Задачи 181–200.Вычислить определенные интегралы.
181. а) 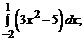 б)
б) 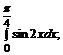 в)
в) 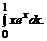
182. а) 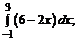 б)
б) 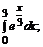 в)
в) 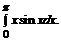
183. а) 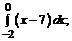 б)
б) 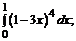 в)
в) 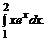
184. а) 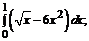 б)
б) 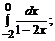 в)
в) 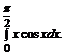
185. а) 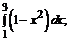 б)
б) 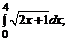 в)
в) 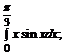
186. а) 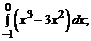 б)
б) 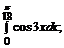 в)
в) 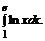
187. а) 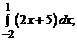 б)
б) 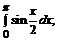 в)
в) 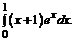
188. а) 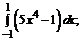 б)
б) 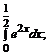 в)
в) 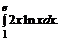
189. а) 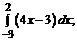 б)
б) 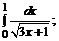 в)
в) 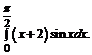
190. а) 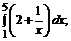 б)
б) 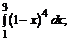 в)
в) 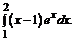
191. а) 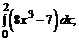 б)
б) 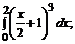 в)
в) 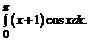
192. а) 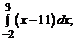 б)
б) 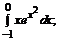 в)
в) 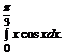
193. а) 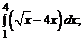 б)
б) 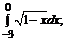 в)
в) 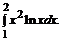
194. а) 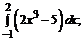 б)
б) 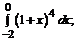 в)
в) 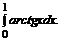
195. а) 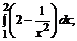 б)
б) 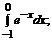 в)
в) 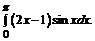
196. а) 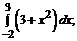 б)
б) 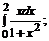 в)
в) 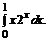
197. а) 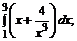 б)
б) 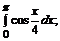 в)
в) 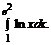
198. а) 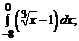 б)
б) 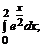 в)
в) 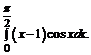
199. а) 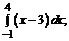 б)
б) 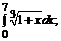 в)
в) 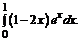
200. а) 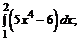 б)
б) 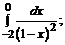 в)
в) 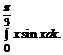
Решение типового примера
При решении примеров рекомендуется использовать свойства определенного интеграла, методы замены переменной и интегрирования по частям в определенном интеграле, а также формулу Ньютона–Лейбница:
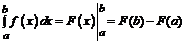 , где
, где 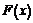 –первообразная для
–первообразная для 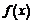 .
.
П р и м е р ы. Вычислить определенные интегралы. 1. 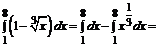
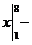
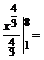

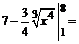

= 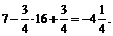
2. 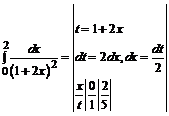 =
= 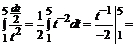
= 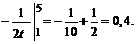
При решении примера применялся метод замены переменной в определенном интеграле.
3. 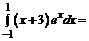
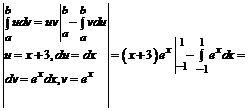
= 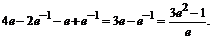
При решении примера применялась формула интегрирования по частям в определенном интеграле.
Задачи 201–220.Вычислить площадь фигуры, ограниченной заданными линиями. Сделать чертеж и заштриховать искомую площадь.
201. 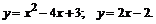
202. 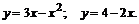
203. 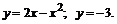
204. 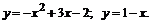
205. 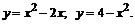
206. 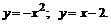
207. 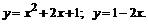
208. 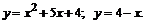
209. 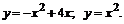
210. 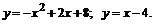
211. 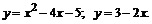
212. 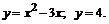
213. 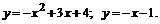
214. 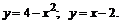
215. 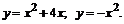
216. 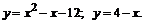
217. 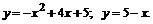
218. 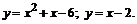
219. 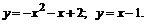
220. 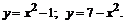
Решение типового примера
П р и м е р. Вычислить площадь фигуры, ограниченную линиями: 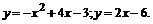
Р е ш е н и е. Построим линии и заштрихуем искомую площадь. Для построения параболы 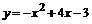 необходимо:
необходимо:
1) найти точки пересечения линии с осью ОХ, решив уравнение 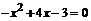 ,
, 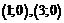 –точки пересечения линии с осью ОХ;
–точки пересечения линии с осью ОХ;
2) найти вершину параболы 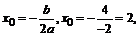 тогда
тогда 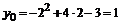 , точка
, точка 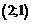 – вершина параболы.
– вершина параболы.
3) найти точку пересечения с осью ОУ: 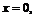 тогда
тогда 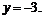
Строим параболу, учитывая что ветви линии направлены вниз. Проводим прямую 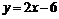 и заштриховываем искомую площадь (рис.2).
и заштриховываем искомую площадь (рис.2).
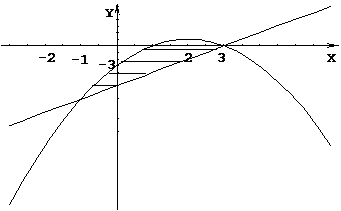
Рис. 2.
Решая уравнение 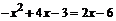 , находим пределы интегрирования
, находим пределы интегрирования 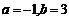 .
.
Вычисляем искомую площадь по формуле 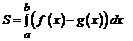 , где
, где 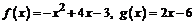 .
.
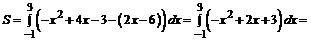
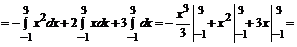
= 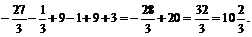
Тема 8. Дифференциальные уравнения первого
Порядка
Обратить внимание на методы решения дифференциальных уравнений первого порядка:
1) с разделяющимися переменными;
2) однородные;
3) линейные.
Усвоить методику нахождения общего и частного решений.
Изучить методы решения линейных однородных и неоднородных дифференциальных уравнений второго порядка со специальной правой частью.
Вопросы для изучения и самопроверки
1. Задачи, приводящие к дифференциальным уравнениям.
2. Основные понятия теории дифференциальных уравнений.
3. Задача Коши.
4. Дифференциальные уравнения первого порядка: с разделяющи- мися переменными, однородные, линейные.
5. Дифференциальные уравнения второго порядка.
6. Однородные дифференциальные уравнения второго порядка с постоянными коэффициентами.
7. Неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами и специальной правой частью.
Задача 221–240.Найти частное решение дифференциального уравнения с разделяющимися переменными, удовлетворяющее заданному начальному условию.
221. 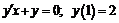 .
.
222. 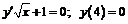 .
.
223. 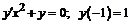 .
.
224. 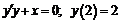 .
.
225. 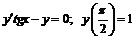 .
.
226. 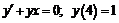 .
.
227. 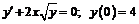 .
.
228. 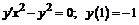 .
.
229. 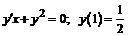 .
.
230. 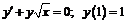 .
.
231. 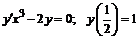 .
.
232. 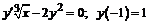 .
.
233. 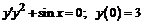 .
.
234. 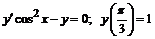 .
.
235. 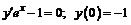 .
.
236. 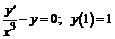 .
.
237. 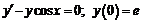 .
.
238. 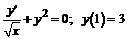
239. 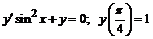 .
.
240. 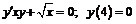 .
.
Решение типового примера
Дифференциальное уравнение первого порядка с разделяющимися переменными имеет вид
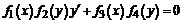 или, с учетом
или, с учетом 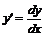 ,
, 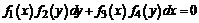 .
.
Разделяем переменные, деля обе части уравнения на произведение 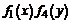 . Интегрируем полученное уравнение с разделенными переменными и получаем общее решение или общий интеграл дифференциального уравнения.
. Интегрируем полученное уравнение с разделенными переменными и получаем общее решение или общий интеграл дифференциального уравнения.
П р и м е р. Найти частное решение дифференциального уравнения с разделяющимиcя переменными, удовлетворяющее заданному начальному условию
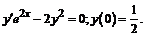
Р е ш е н и е. Подставляем в уравнение 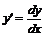 и получаем
и получаем 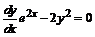 или
или 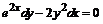 . Делим обе части уравнения на произведение
. Делим обе части уравнения на произведение 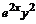 , получаем уравнение с разделенными переменными
, получаем уравнение с разделенными переменными 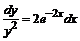 . Интегрируя обе части, получаем общее решение:
. Интегрируя обе части, получаем общее решение: 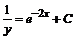 или
или 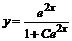 .
.
Подставляем начальное условие 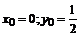 в общее решение
в общее решение 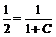 , отсюда
, отсюда 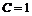 .
.
Подставляем найденное значение произвольной постоянной 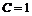 в общее решение и получаем искомое частное решение
в общее решение и получаем искомое частное решение 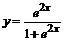 .
.
Задачи 241–260.Найти частное решение линейного дифференциального уравнения первого порядка, удовлетворяющее заданному начальному условию.
241. 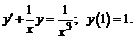

242. 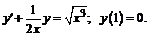
243. 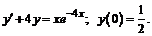
244. 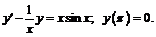
245. 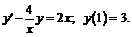
246. 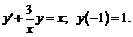
247. 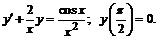
248. 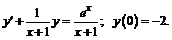
249. 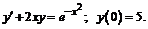
250. 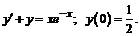
251. 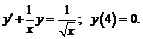
252. 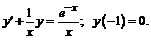
253. 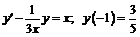 .
.
254. 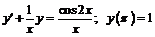 .
.
255. 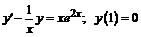
256. 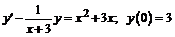 .
.
257. 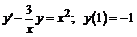 .
.
258. 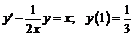 .
.
259. 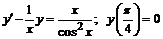 .
.
260. 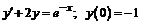 .
.
Решение типового примера
Линейным дифференциальным уравнением первого порядка называется уравнение вида:
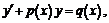 где
где 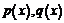 – данные непрерывные функции.
– данные непрерывные функции.
При решении уравнения применяем подстановку 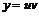 , где
, где 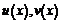 – искомые дифференцируемые функции. Подcтавляя вместо производной
– искомые дифференцируемые функции. Подcтавляя вместо производной  , получаем уравнение
, получаем уравнение
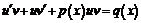 или
или 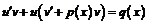 .
.
Подбираем 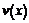 так, чтобы выражение в скобках обращалось в ноль, тогда данное уравнение преобразуется к двум уравнениям с разделяющимися переменными
так, чтобы выражение в скобках обращалось в ноль, тогда данное уравнение преобразуется к двум уравнениям с разделяющимися переменными 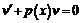 и
и 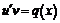 .
.
П р и м е р. Найти частное решение линейного дифференциального уравнения первого порядка, удовлетворяющее заданному начальному условию 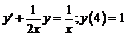 .
.
Р е ш е н и е.Подставляем 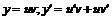 в данное уравнение
в данное уравнение 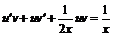 , или
, или 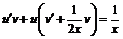 . Получаем два уравнения с разделяющимися переменными
. Получаем два уравнения с разделяющимися переменными 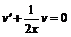 и
и 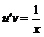 . Из первого уравнения находим функцию
. Из первого уравнения находим функцию 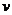 , подставляя
, подставляя 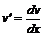 , имеем
, имеем 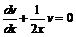 или
или 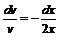 . Интегрируя уравнение, получаем
. Интегрируя уравнение, получаем 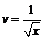 .
.
Из второго уравнения находим функцию 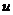 ,
, 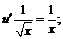 подставляя
подставляя 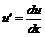 , имеем
, имеем 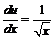 или
или 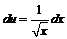 . Интегрируя уравнение, получаем
. Интегрируя уравнение, получаем 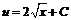
 .
.
Найденные функции подставляем в выражение 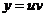 , находим общее решение исходного дифференциального уравнения
, находим общее решение исходного дифференциального уравнения 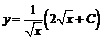 или
или 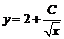 .
.
Подставляем начальное условие 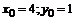 в общее решение, получаем
в общее решение, получаем 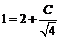 , отсюда
, отсюда 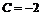 .
.
Найденное значение произвольной постоянной 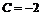 подставляем в общее решение, получаем искомое частное решение
подставляем в общее решение, получаем искомое частное решение 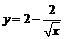 .
.
Тема 9. ОСНОВНЫЕ ПОНЯТИЯ И ЗАДАЧИ ТЕОРИИ
ВЕРОЯТНОСТЕЙ
Для успешного решения задач по этой теме необходимо обратить внимание на определения основных понятий теории вероятностей, вероятности появления события. Особое внимание следует уделить классификации событий, теоремам сложения и умножения вероятностей. Далее необходимо остановиться на применении формулы полной вероятности и формулы Байеса, усвоить понятие повторных независимых испытаний, а также применения формулы Бернулли и предельных теорем Муавра–Лапласа и Пуассона.
Глубокое усвоение понятия случайной величины, ее законов распределения и числовых характеристик является необходимым условием изучения методов обработки данных.
Вопросы для изучения и самопроверки
1. Предмет теории вероятностей.
2. Основные понятия (пространство элементарных событий, классификация событий).
3. Классическое определение вероятности случайного события.
4. Теоремы сложения и умножения вероятностей.
5. Формула полной вероятности. Формула Баесса.
6. Схема повторных испытаний. Формула Бернулли.
7. Локальная и интегральная формулы Лапласа. Формула Пуассона.
8. Понятие случайной величины. Закон распределения дискретной случайной величины.
9. Числовые характеристики случайной величины.
10. Непрерывная случайная величина. Функция распределения. Плотность вероятности.
11. Нормальный закон распределения и его свойства.
12. Вероятность попадания нормально распределенной случайной величины в заданный интервал.
Задачи 261–280. При решении задач следует использовать теоремы сложения и умножения вероятностей.
261. Для сигнализации об аварии установлены два независимо работающих сигнализатора. Вероятность того, что при аварии сработает первый сигнализатор, равна 0,9; второй сигнализатор срабатывает с вероятностью 0,85. Найти вероятность того, что при аварии сработает только один сигнализатор.
262. Отдел технического контроля проверяет изделия на стандартность. Вероятность того, что наугад взятое изделие окажется бракованным, равна 0,12. Проверено три изделия. Какова вероятность того, что два из них бракованные?
263. В группе учащихся, состоящей из 25 человек, 15 юношей и 10 девушек, для дежурства случайным образом отобрано двое студентов. Какова вероятность того, что среди них будет один юноша и одна девушка?
264. В ящике имеется 14 деталей, из которых 6 деталей нестандартны. Сборщик наудачу извлекает из ящика 4 детали. Какова вероятность того, что все они будут нестандартны?
265.Студент знает 20 из 25 вопросов программы. Какова вероятность того, что он знает все три вопроса, предложенные экзаменатором?
266. Техническое устройство содержит три независимо работающих элемента. Вероятности отказа этих элементов соответственно равны 0,06; 0,08 и 0,1. Найти вероятность того, что техническое устройство не сработает, если для этого достаточно, чтобы отказал хотя бы один элемент.
267. Для поражения цели достаточно одного попадания. По цели произведено три выстрела с вероятностями попадания 0,78; 0,84; 0,92 соответственно. Найти вероятность того, что цель будет поражена.
268. Вероятность попадания в мишень при трех выстрелах хотя бы один раз для некоторого стрелка равна 0,875. Найти вероятность попадания при одном выстреле.
269. Из партии изделий товаровед отбирает изделия высшего сорта. Вероятность того, что наудачу взятое изделие окажется высшего сорта, равна 0,4. Найти вероятность того, что из трех проверенных изделий только два будут высшего сорта.
270. Студент разыскивает нужные ему сведения в трех справочниках. Вероятности того, что эти сведения находятся в первом, во втором и в третьем справочнике равны соответственно 0,6; 0,8; 0,9. Найти вероятность того, что требуемые сведения содержатся хотя бы в одном справочнике.
271. В урне находятся 18 шаров, шесть из которых синие, а остальные белые. Наудачу друг за другом извлекаются три шара. Какова вероятность того, что все они будут синими?
272. В первой коробке 3 белых и 10 голубых шарфов. Во второй коробке 7 белых и 2 голубых шарфа. Из каждого ящика наудачу вынули по шарфу. Какова вероятность, что оба шарфа белые?
273. Три стрелка производят выстрел по цели. Вероятность попадания в цель для первого стрелка равна 0,7, для второго — 0,85, для третьего — 0,9. Найти вероятность того, что произойдет не менее двух попаданий.
274. В ящике 20 шаров, из которых 9 красных, а остальные белые. Наудачу вынули три шара. Какова вероятность того, что все они белые?
275. Имеется четыре прибора. Вероятность того, что прибор неисправен, равна 0,2. Какова вероятность того, что хотя бы один из четырех приборов исправен?
276. В группе из 23 студентов имеется 7 отличников. Выбираются наудачу три студента. Какова вероятность, что все они отличники?
277. В ящике находятся 13 деталей, четыре из которых бракованные. Наудачу отобраны три детали. Какова вероятность того, что все они не окажутся бракованными?
278. Имеются два ящика, в первом из которых 6 белых и 9 красных платков, а во втором — 4 белых и 2 красных платка. Из каждого ящика вынимается наудачу по одному платку. Какова вероятность того, что один из них будет красным, а другой белым?
279. Вероятность выхода из строя комбайна в течение одного рабочего дня равна 0,01. Какова вероятность того, что за три рабочих дня комбайн ни разу не выйдет из строя?
280. Вероятность обнаружения цели при одном цикле обзора радиолокационной станцией равна 0,4. Какова вероятность обнаружения цели хотя бы один раз при трех циклах обзора?
Решение типовых примеров
П р и м е р 1. Три стрелка производят по одному выстрелу в цель независимо друг от друга. Вероятности попадания в цель для каждого из них равны соответственно 0,7; 0,8; 0,9. Найти вероятность того, что: а) в цель попадет только один стрелок; б) в цель попадут только два стрелка; в) в цель попадет хотя бы один стрелок.
Решение. а) Рассмотрим следующие события:
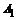 – первый стрелок попал в цель;
– первый стрелок попал в цель;
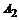 – второй стрелок попал в цель;
– второй стрелок попал в цель;
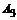 – третий стрелок попал в цель;
– третий стрелок попал в цель;
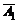 – первый стрелок не попал в цель;
– первый стрелок не попал в цель;
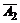 – второй стрелок не попал в цель;
– второй стрелок не попал в цель;
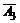 – третий стрелок не попал в цель.
– третий стрелок не попал в цель.
По условию Р(А1,) =0,7; Р(А2) =0,8; Р(А3) =0,9; 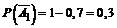 ;
; 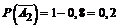 ;
; 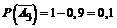 .
.
Пусть событие В – попал только один стрелок. Тогда
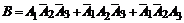 .
.
Отсюда в силу несовместности событий-слагаемых и независимости событий-сомножителей
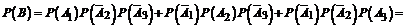
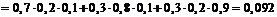 .
.
б) Пусть событие С – попадут только два стрелка. Тогда
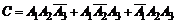 .
.
Отсюда Р(С) =0,7∙0,8∙0,1 + 0,7∙0,2∙ 0,9+0,3∙0,8∙0,9 = 0,398.
в) Пусть событие –Е попал хотя бы один стрелок. Тогда противоположное событие 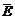 – не попал ни один из них, т. е.
– не попал ни один из них, т. е. 
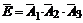 . Поэтому Р(
. Поэтому Р( 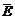 ) =0,3∙0,2∙0,1=0,006.
) =0,3∙0,2∙0,1=0,006.
Отсюда Р(Е) = 1-Р 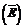 = 1-0,006 = 0,994.
= 1-0,006 = 0,994.
П р и м е р 2. Среди 15 микрокалькуляторов, имеющихся в вычислительной лаборатории, лишь 6 новых, а остальные – бывшие в употреблении. Наугад взято три микрокалькулятора. Какова вероятность, что все они окажутся новыми?
Решение. Рассмотрим события:
А – первый из взятых микрокалькуляторов новый;
В – второй микрокалькулятор новый;
С – третий микрокалькулятор новый.
Тогда Р(А) = 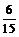 .
.
Вероятность того, что второй микрокалькулятор будет новый, при условии, что первым уже был отобран новый микрокалькулятор, т. е. условная вероятность события В, равна
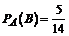 .
.
Вероятность того, что третьим будет отобран новый микрокалькулятор, при условии, что уже отобраны два новых микрокалькулятора, т. е. условная вероятность события С, равна
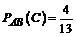 .
.
Искомая вероятность того, что все три отобранных микрокалькулятора окажутся новыми, равна
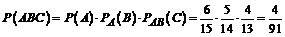 .
.
Задачи 281–300.При решении задач следует использовать формулу полной вероятности и формулы Байеса.
281. Изделие проверяется на стандартность одним из двух товароведов. Первый товаровед проверяет 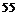 % изделий, второй –
% изделий, второй – 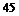 %. Вероятности того, что изделие будет признано стандартным, равны соответственно
%. Вероятности того, что изделие будет признано стандартным, равны соответственно 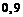 и
и 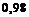 для первого и второго товароведов. При проверке изделие было признано стандартным. Найти вероятность того, что это изделие проверил второй контролер.
для первого и второго товароведов. При проверке изделие было признано стандартным. Найти вероятность того, что это изделие проверил второй контролер.
282. На сборку телевизоров поступают микросхемы от двух поставщиков, причем 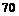 % микросхем поступает от первого поставщика, а
% микросхем поступает от первого поставщика, а 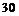 % – от второго. Брак среди микросхем первого поставщика составляет
% – от второго. Брак среди микросхем первого поставщика составляет 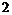 %, второго –
%, второго – 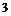 %. Какова вероятность того, что взятая наудачу микросхема окажется без брака?
%. Какова вероятность того, что взятая наудачу микросхема окажется без брака?
283. В магазин на продажу поступили электролампочки с трех заводов. Известно, что среди лампочек первого завода 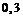 % брака, второго –
% брака, второго – 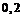 %, третьего –
%, третьего – 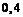 % брака. Найти вероятность покупки годной электролампочки, если с первого завода поступило
% брака. Найти вероятность покупки годной электролампочки, если с первого завода поступило 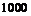 лампочек, со второго –
лампочек, со второго – 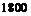 и с третьего –
и с третьего – 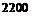 электролампочек.
электролампочек.
284. На склад поступает продукция двух фабрик, причем доля продукции первой фабрики составляет 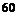 %, второй –
%, второй – 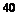 %. Средний процент нестандартных изделий в продукции первой фабрики равен
%. Средний процент нестандартных изделий в продукции первой фабрики равен 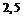 %, второй –
%, второй – 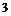 %. Найти вероятность того, что наудачу взятое изделие произведено на первой фабрики, если оно оказалось стандартным.
%. Найти вероятность того, что наудачу взятое изделие произведено на первой фабрики, если оно оказалось стандартным.
285. На трех автоматических станках изготавливаются одинаковые детали. Известно, что 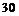 % продукции производится первым станком,
% продукции производится первым станком, 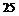 % вторым и
% вторым и 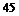 % третьим. Вероятность изготовления детали, отвечающей стандарту, на первом станке равна
% третьим. Вероятность изготовления детали, отвечающей стандарту, на первом станке равна 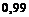 , на втором –
, на втором – 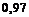 , на третьем –
, на третьем – 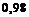 . Определить вероятность того, что взятая наугад деталь из нерассортированной продукции не соответствует стандарту.
. Определить вероятность того, что взятая наугад деталь из нерассортированной продукции не соответствует стандарту.
286. В группе из  стрелков имеются
стрелков имеются 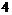 отличных,
отличных, 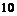 хороших и 6 посредственных стрелков. На линию огня наугад вызывается стрелок и производит один выстрел. Найти вероятность поражения цели, если известно, что вероятности поражения цели для отличного, хорошего и посредственного стрелка равны соответственно
хороших и 6 посредственных стрелков. На линию огня наугад вызывается стрелок и производит один выстрел. Найти вероятность поражения цели, если известно, что вероятности поражения цели для отличного, хорошего и посредственного стрелка равны соответственно 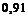 ,
, 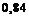 и
и 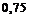 .
.
287. В канцелярии работают три секретарши, которые отправляют соответственно 40, 35 и 25% бумаг. Первая секретарша правильно адресует бумаги с вероятностью 0,94, вторая – 0,98, третья – 0,92. Найти вероятность того, что верно адресованный документ отправлен второй секретаршей.
288. В трех одинаковых урнах содержится по 10 шаров. В первой урне находятся 6 белых и 4 черных шара, во второй –3 красных и 7 черных шаров, а в третьей – 2 белых и 8 черных шаров. Какова вероятность извлечения черного шара из наудачу выбранной урны?
289. В телевизионном ателье имеются 10 кинескопов первого типа и 15 кинескопов второго. Вероятности того, что кинескопы выдержат гарантийный срок службы, равны соответственно 0,88 и 0,79. Взятый наудачу кинескоп выдержал гарантийный срок. Какова вероятность того, что он принадлежит партии кинескопов первого типа?
290. В четырех корзинах находится картофель. В первой корзине имеется 4% поврежденных клубней, во второй – 9%, в третьей – 7%, а в четвертой – 5%. Какова вероятность извлечения неповрежденного клубня из наугад выбранной корзины?
291. На наблюдательной станции установлены три радиолокатора. Вероятность обнаружения цели первым локатором равна 0,79, вто -
рым – 0,85, третьим – 0,91. Найти вероятность обнаружения цели наугад включенным радиолокатором.
292. В учебной лаборатории имеются 14 измерительных приборов первого типа и 6 второго типа. Вероятность безотказной работы во время опыта первого прибора равна 0,82, а второго – 0,94. При проведении опыта наудачу выбранный прибор работал безотказно. Какова вероятность того, что он является прибором первого типа?
293. По линии связи передается 80% сигналов типа А и 20% типа В. В среднем принимается 55% сигналов типа A и 69% типа B. Посланный сигнал был принят. Найти вероятность того, что этот сигнал типа А.
294. Для участия в студенческих соревнованиях выделено 10 человек из первой группы, 8 из второй, 7 из третьей. Вероятности попадания в сборную команду академии равны соответственно 0,8, 0,7 и 0,65 для студентов первой, второй и третьей группы. Какова вероятность того, что случайно выбранный студент попадет в сборную команду?
295. На участке, изготовляющем болты, первый станок производит 25%, второй – 32%, третий – 43% всех изделий. В продукции каждого станка брак составляет 5%, 4,5%, 2,6% изделий, произведенных на первом, втором и третьим станках соответственно. Найти вероятность того, что случайно взятый дефектный болт изготовлен на первом станке.
296. В двух ящиках с 30 шарами в каждом содержится по 6 красных шаров, а в четырех других с 15 шарами в каждом – по 3 красных шара. Найти вероятность того, что из наугад взятого ящика вынули красный шар.
297. Пассажир может обратиться за получением билета в одну из трех касс вокзала №1 или в одну из пяти касс вокзала №2. Вероятность наличия билета к моменту прихода пассажира в кассе вокзала №1 равна 0,72, а в кассе вокзала №2 – 0,67. Найти вероятность покупки билета пассажиром в наугад выбранной кассе.
298. На трех станках обрабатываются однотипные детали. Вероятности брака для первого, второго и третьего станка равны соответственно 0,015; 0,021 и 0,018. Обработанные детали складываются в один ящик. Производительности станков относятся как 3:2:5. Определить вероятность того, что взятая наудачу деталь из ящика будет бракованной.
299. Автомашина используется для перевозки товара в три магазина. В первом магазине разгрузка в течение 30 минут выполняется с вероятностью 0,76, во втором – 0,84, а в третьем – 0,63. На базу сообщили, что машина разгружена за 30 минут. Какова вероятность того, что это произошло в первом магазине?
300. Литье в болванках поступает из трех заготовительных цехов: 30% из первого цеха, 42% из второго и 28% из третьего цеха. При этом в продукции первого цеха имеется 5% брака, второго – 8,5% брака, а третьего – 4% брака. Найти вероятность того, что взятая наугад болванка окажется без дефектов.
Решение типового примера
Пусть события 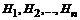 образуют полную группу событий с заданными вероятностями и называются гипотезами. Событие
образуют полную группу событий с заданными вероятностями и называются гипотезами. Событие 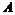 появляется с одной из этих гипотез с заданными вероятностями. Тогда вероятность события
появляется с одной из этих гипотез с заданными вероятностями. Тогда вероятность события 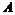 вычисляется по формуле полной вероятности
вычисляется по формуле полной вероятности 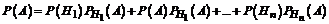 .
.
Если известно, что в результате испытания появилось событие 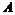 , то вероятность того , что оно произошло именно с гипотезой
, то вероятность того , что оно произошло именно с гипотезой 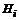 , вычисляется по формулам Байеса
, вычисляется по формулам Байеса 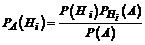 , где
, где 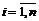 .
.
П р и м е р. На базу поступает 26% продукции с первой фабрики, 32% со второй и 42% с третьей фабрики. Известно, что средний процент нестандартных изделий для продукции первой фабрики равен 6%, для второй – 2% и для третьей – 2,5%. Найти вероятность того, что наудачу взятое с базы изделие произведено на первой фабрики, если оно оказалось стандартным.
Р е ш е н и е. Обозначим события – гипотезы:
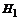 – изделие произведено на первой фабрике;
– изделие произведено на первой фабрике;
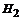 – изделие произведено на второй фабрике;
– изделие произведено на второй фабрике;
 – изделие произведено на третьей фабрике.
– изделие произведено на третьей фабрике.
Из условия задачи найдем вероятности этих событий: 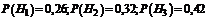 .
.
Событие 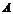 – наудачу взятое изделие оказалось стандартным, может произойти с одной из этих гипотез с вероятностями:
– наудачу взятое изделие оказалось стандартным, может произойти с одной из этих гипотез с вероятностями: 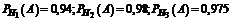 .
.
Вычисляем вероятность события 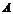 по формуле полной вероятности:
по формуле полной вероятности: 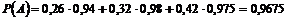 .
.
Вероятность того, что наудачу взятое стандартное изделие произведено именно на первой фабрике, вычисляем по формуле Байеса: 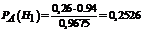 . Значит, 25,26% всех стандартных изделий на базе принадлежат продукции первой фабрики.
. Значит, 25,26% всех стандартных изделий на базе принадлежат продукции первой фабрики.
Задачи 301–320.При решении задач необходимо использовать формулу Бернулли или асимптотические формулы в схеме повторных испытаний.
301. Вероятность выиграть по одному билету лотереи равна 1/7. Какова вероятность, имея 6 билетов, выиграть: а) по двум билетам;
б) не менее четырех?
302. Вероятность попадания в цель, при одном выстреле равна 0,4. Найти вероятность ровно 100 попаданий из 320 выстрелов.
303. Найти вероятность того, что при 600 подбрасываниях игральной кости число 4 выпадет не менее 90 раз и не более 120 раз.
304. В партии из 1000 изделий имеется 10 дефектных. Найти вероятность того, что среди 50 изделий, взятых наудачу из этой партии, ровно три окажутся дефектными.
305. Всхожесть семян данного растения составляет 90%. Найти вероятность того, что из пяти посеянных семян взойдут: а) четыре; б) не более трех.
306. На каждые 10 клубней собранного картофеля в среднем приходится 6 крупных. Наудачу выбрано 4 клубня. Найти вероятность того, что среди них окажется крупных: а) не менее трех, б) два.
307. В ремонтной мастерской имеется 4 мотора. Для каждого мотора вероятность того, что он в данный момент включен
