Производная параметрически заданной функции
Не напрягаемся, в этом параграфе тоже всё достаточно просто. Можно записать общую формулу параметрически заданной функции, но, для того, чтобы было понятно, я сразу запишу конкретный пример. В параметрической форме функция задается двумя уравнениями: 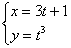 . Частенько уравнения записывают не под фигурными скобками, а последовательно:
. Частенько уравнения записывают не под фигурными скобками, а последовательно: 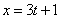 ,
, 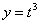 .
.
Переменная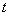 называется параметром и может принимать значения от «минус бесконечности» до «плюс бесконечности». Рассмотрим, например, значение
называется параметром и может принимать значения от «минус бесконечности» до «плюс бесконечности». Рассмотрим, например, значение 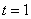 и подставим его в оба уравнения:
и подставим его в оба уравнения: 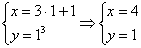 . Или по человечески: «если икс равен четырем, то игрек равно единице». На координатной плоскости можно отметить точку
. Или по человечески: «если икс равен четырем, то игрек равно единице». На координатной плоскости можно отметить точку 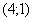 , и эта точка будет соответствовать значению параметра
, и эта точка будет соответствовать значению параметра 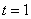 ..
..
В простейших случаях есть возможность представить функцию в явном виде. Выразим из первого уравнения параметр: 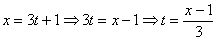 – и подставим его во второе уравнение:
– и подставим его во второе уравнение: 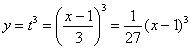 . В результате получена обыкновенная кубическая функция.
. В результате получена обыкновенная кубическая функция.
В более «тяжелых» случаях такой фокус не прокатывает. Но это не беда, потому что для нахождения производной параметрической функции существует формула:
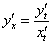 Находим производную от «игрека по переменной тэ»:
Находим производную от «игрека по переменной тэ»: 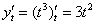
Все правила дифференцирования и таблица производных справедливы, естественно, и для буквы 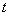 , таким образом, какой-то новизны в самом процессе нахождения производных нет. Просто мысленно замените в таблице все «иксы» на букву «тэ».
, таким образом, какой-то новизны в самом процессе нахождения производных нет. Просто мысленно замените в таблице все «иксы» на букву «тэ».
Находим производную от «икса по переменной тэ»: 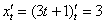
Теперь только осталось подставить найденные производные в нашу формулу: 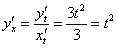
Готово. Производная, как и сама функция, тоже зависит от параметра 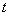 .
.
Что касается обозначений, то в формуле вместо записи 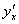 можно было просто записать
можно было просто записать 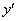 без подстрочного индекса, поскольку это «обычная» производная «по икс». Но в литературе всегда встречается вариант
без подстрочного индекса, поскольку это «обычная» производная «по икс». Но в литературе всегда встречается вариант 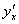 , поэтому я не буду отклоняться от стандарта.
, поэтому я не буду отклоняться от стандарта.
Пример 6
Найти производную от функции, заданной параметрически 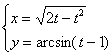
Используем формулу 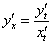
В данном случае:
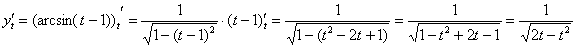
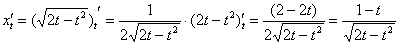
Таким образом:
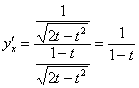
Особенностью нахождения производной параметрической функции является тот факт, что на каждом шаге результат выгодно максимально упрощать. Так, в рассмотренном примере при нахождении 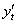 я раскрыл скобки под корнем (хотя мог этого и не делать). Велик шанс, что при подстановке
я раскрыл скобки под корнем (хотя мог этого и не делать). Велик шанс, что при подстановке 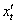 и
и 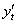 в формулу многие вещи хорошо сократятся. Хотя встречаются, конечно, примеры и с корявыми ответами.
в формулу многие вещи хорошо сократятся. Хотя встречаются, конечно, примеры и с корявыми ответами.
Пример 8
Найти первую и вторую производные от функции, заданной параметрически 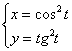
Сначала найдем первую производную.
Используем формулу 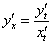
В данном случае:
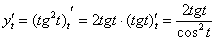
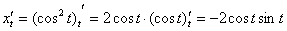
Подставляет найденные производные в формулу. В целях упрощений используем тригонометрическую формулу 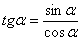 :
:
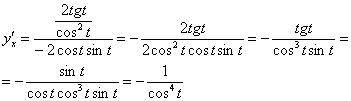
Я заметил, что в задаче на нахождение производной параметрической функции довольно часто в целях упрощений приходится использовать тригонометрические формулы. Помните их или держите под рукой, и не пропускайте возможность упростить каждый промежуточный результат и ответы. Зачем? Сейчас нам предстоит взять производную от 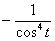 , и это явно лучше, чем находить производную от
, и это явно лучше, чем находить производную от 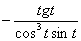 . Найдем вторую производную. Используем формулу:
. Найдем вторую производную. Используем формулу: 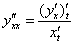 .
.
Посмотрим на нашу формулу. Знаменатель 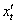 уже найден на предыдущем шаге. Осталось найти числитель – производную от первой производной по переменной «тэ»:
уже найден на предыдущем шаге. Осталось найти числитель – производную от первой производной по переменной «тэ»: 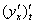
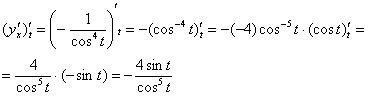
Осталось воспользоваться формулой:
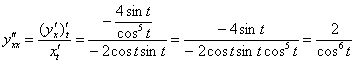
Пример 9
Найти 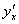 и
и 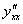 для функции, заданной параметрически
для функции, заданной параметрически 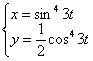
Пример 10
Найти 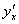 и
и 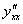 для функции, заданной параметрически
для функции, заданной параметрически 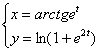
Пример 9: Решение: Найдем первую производную.
Используем формулу: 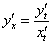 . В данном случае:
. В данном случае:
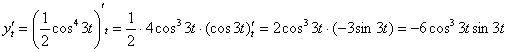
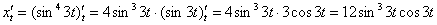
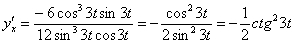
Найдем вторую производную, используя формулу 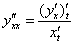 .
.
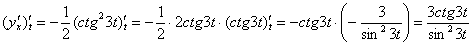
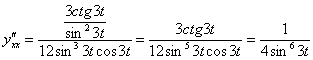
Пример 10: Решение:
Используем формулу: 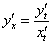 . В данном случае:
. В данном случае:
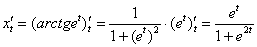
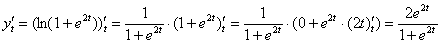
Таким образом:
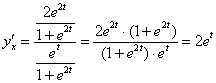
Вторая производная:
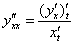
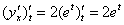
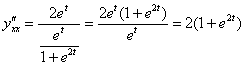
28. Касательная и нормаль к линии. --------------------
