Понятие дифференциала функции одной переменной и его геометрический смысл.
Понятие и геометрический смысл дифференциала
Определение. Дифференциалом функции в некоторой точке x называется главная, линейная часть приращения функции.
Дифференциал функции y = f(x) равен произведению её производной на приращение независимой переменной x (аргумента).
Это записывается так: 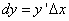 или
или 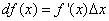 или же
или же 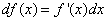
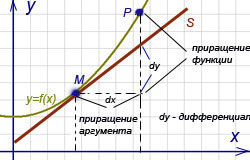
Геометрический смысл дифференциала. Дифференциал функции y = f(x) равен приращению ординаты касательной S, проведённой к графику этой функции в точке M(x; y), при изменении x (аргумента) на величину 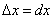 (см. рисунок).
(см. рисунок).
Почему дифференциал можно использовать в приближенных вычислениях?
Дифференциал, 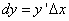 является главной, линейной относительно
является главной, линейной относительно 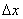 частью приращения функции; чем меньше
частью приращения функции; чем меньше 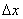 , тем большую долю приращения составляет эта часть. В этом можно убедиться, мысленно передвигая перпендикуляр, опущенный из точки P (см. рисунок) к оси Ox, ближе к началу координат. Поэтому при малых значениях
, тем большую долю приращения составляет эта часть. В этом можно убедиться, мысленно передвигая перпендикуляр, опущенный из точки P (см. рисунок) к оси Ox, ближе к началу координат. Поэтому при малых значениях 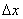 (и при
(и при 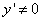 ) приращение функции можно приближенно заменить его главной частью
) приращение функции можно приближенно заменить его главной частью 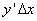 , т.е.
, т.е. 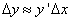
О разных формах записи дифференциала Дифференциал функции в точке x и обозначают 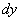 или
или 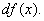 Следовательно,
Следовательно, 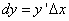 (1) или
(1) или 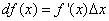 (2)
(2)
поскольку дифференциал функции y = f(x) равен произведению её производной на приращение независимой переменной. Замечание. Нужно помнить, что если x – исходное значение аргумента, а 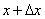 - наращенное значение, то производная в выражении дифференциала берётся в исходной точке x ; в формуле (1) этого не видно из записи.Дифференциал функции можно записать в другой форме:
- наращенное значение, то производная в выражении дифференциала берётся в исходной точке x ; в формуле (1) этого не видно из записи.Дифференциал функции можно записать в другой форме: 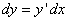 (3)
(3)
или 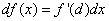 (4)
(4)
30. Свойства дифференциала.
Свойства дифференциала
Дифференциал обладает свойствами, аналогичными свойствам производной:
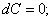 (С – постоянная величина) (5)
(С – постоянная величина) (5)
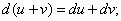 (6)
(6) 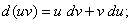 (7)
(7)
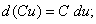 (8)
(8) 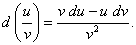 (9)
(9)
Формулы (5) – (9) получаются из соответствующих формул для производной умножением обеих частей каждого равенства на 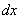 .
.
Применение дифференциала в приближенных вычислениях
Установленное во втором параграфе приближенное равенство
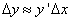 или
или 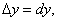 (10)
(10)
позволяет использовать дифференциал для приближенных вычислений значений функции.
Запишем приближенное равенство более подробно. Так как
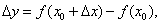 а
а 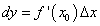 то
то 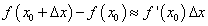 или
или
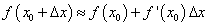 (11)
(11)
Абсолютная и относительная погрешности приближенных вычислений
Пользуясь приближенным значением числа, нужно иметь возможность судить о степени его точности. С этой целью вычисляют его абсолютную и относительную погрешности.
Абсолютная погрешность  приближенного числа
приближенного числа 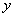 равна абсолютной величине разности между точным числом
равна абсолютной величине разности между точным числом 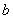 и его приближенным значением:
и его приближенным значением: 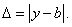 (12)
(12)
Относительной погрешностью 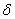 приближенного числа
приближенного числа 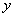 называется отношение абсолютной погрешности этого числа к абсолютной величине соответствующего точного числа:
называется отношение абсолютной погрешности этого числа к абсолютной величине соответствующего точного числа:
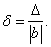 (13) Если точное число неизвестно, то
(13) Если точное число неизвестно, то 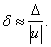 (14)
(14)
Иногда, прежде чем применить формулу (11), требуется предварительно преобразовать исходную величину. Как правило, это делается в двух целях. Во-первых, надо добиться, чтобы величина 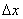 была достаточно малой по сравнению с
была достаточно малой по сравнению с 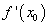 , так как чем меньше
, так как чем меньше 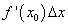 , тем точнее результат приближенного вычисления. Во-вторых, желательно, чтобы величина
, тем точнее результат приближенного вычисления. Во-вторых, желательно, чтобы величина 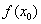 вычислялась просто.
вычислялась просто.
31. Применение дифференциала к приближенным вычислениям.
Как уже известно, приращение ∆у функции у=ƒ(х) в точке х можно представить в виде ∆у=ƒ'(х)•∆х+α•∆х, где α→0 при ∆х→0, или ∆у=dy+α•∆х. Отбрасывая бесконечно малую α•∆х более высокого порядка, чем ∆х, получаем приближенное равенство ∆у≈dy, (3)
причем это равенство тем точнее, чем меньше ∆х.
