Показателей безопасности полетов

С помощью вероятностных показателей безопасности поле­тов могут быть решены следующие задачи:

1. Оценка влияния на БзП отдельного опасного фактора или некоторой совокупности опасных факторов.

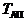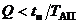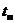2. Отработка требований к уровню БзП для проектируемого ЛА на основании опыта эксплуатации прототипа. Если известен – средний налет на одно АП для прототипа, то для проек­тируемого ЛА уровень риска на основании выражения (1.11) должен удовлетворять условию , где – пред­полагаемая продолжительность полета проектируемого ЛА.

3. Выполнение расчетов по оценке уровня безопасности поле­тов для проектируемого ЛА.

4. Оптимальное распределение заданного уровня риска между функциональными системами ЛА по критерию стоимости (мате­риальным затратам, массы ЛА и т.д.) в процессе проектирова­ния ЛА.

5. Определение соответствия фактического уровня БзП заданному. В принципе эта задача решается аналогично второй задаче, только здесь исходной информацией является величина заданно­го уровня риска. Текущее значение 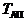должно сравниваться в соответствии с выражением (1.11) с заданным уровнем риска.

6. Оценка эффективности мероприятий и доработок на авиа­ционной технике, направленных на повышение БзП, еще до их практической реализации.

Пример. Пусть в результате выполнения доработок вероят­ность отказа двигателя в полете уменьшилась в два раза. Тре­буется оценить эффективность доработок при выполнении 100000 полетов. Полагая 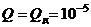, определяем по формуле (1.5):

.

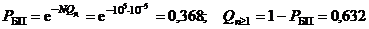После выполнения доработок

;

.

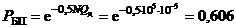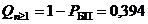Доработка дала значительный положительный эффект, ве­роятность благополучного завершения рассматриваемого числа полетов возросла в 1,64 раза.

7. Отыскание наиболее слабых мест в обеспечении БзП и раз­работка эффективных мероприятий для ее повышения.

8. Оптимизация уровня БзП с учетом стоимости и эффектив­ности.

Для иллюстрации возможностей решения такой задачи рассмотрим элементарный пример. Предположим, что на созда­ние нового летательного аппарата отпущено А средств, стои­мость В одного ЛА в зависимости от уровня риска выражается формулой

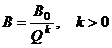. (1.52)

График соответствующей зависимости (1.52) изображен на

рис.1.10. Требуется определить уровень риска 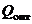, соот­ветствующий максимуму величины 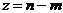, где 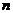– число построенных ЛА; 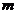– число ЛА, потерянных от АП за время полета, соответ­ствующего установленному для ЛА ресурсу . Таким обра­зом, в данной задаче в качестве критерия эффективности при­нимается величина 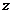. Предполагается, что при выбранном крите­рии эффективности ЛА удовлетворяет требованиям, предъявляе­мым к нему в соответствии с целевым назначением. 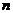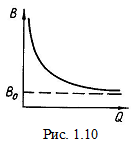Величина определяется по формуле 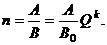Величина 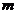может быть определена в предположении пуассоновского закона распределения числа АП как среднее значение числа АП, то есть

,

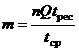где 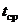– средняя продолжительность одного полета.

Тогда

.

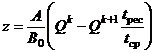Взяв производную от 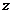по и приравняв ее к нулю, определим из полученного равенства

.

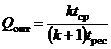Полученное значение 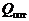соответствует максимуму величины 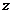, что подтверждается знаком второй производной:

.

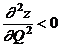Из результатов решения этой задачи следуют два вывода:

1) постановка вопроса об определении оптимального уровня риска с учетом стоимости ЛА правомерна;

2) этот уровень безопасности полетов должен задаваться с учетом назначенного ресурса ЛА, причем чем больше ресурс, тем больше должен задаваться уровень безопасности полетов.