Степенные ряды. Интервал и радиус сходимости

Степенным рядом называется функциональный ряд вида

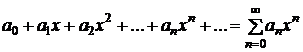, (3.16)

где 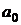, , 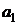, 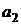…, , … 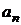– постоянные числа, называемые коэффициентами ряда.

Часто рассматривают степенные ряды более общего вида

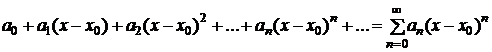, (3.17)

частным случаем которых при 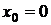являются степенные ряды (3.16). С другой стороны, каждый степенной ряд вида (3.17) с помощью замены переменной 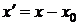сводится к ряду вида (3.16).

При 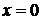(соответственно, при 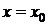) всякий степенной ряд вида (3.16) (соответственно, вида (3.17)) сходится, поэтому область сходимости степенного ряда содержит по крайней мере одну точку.

Теорема Абеля:

1) Если степенной ряд 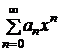сходится в точке 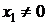, то он абсолютно сходится в каждой точке , для которой ;

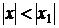2) Если степенной ряд 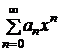расходится при некотором значении 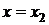, то он расходится и при всех значениях , для которых .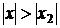

Интервалом сходимости степенного ряда вида (3.16) (соответственно, вида (3.17)) называется такой интервал 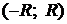(соответственно, 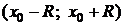), что в каждой его точке ряд сходится абсолютно, а в каждой точке, лежащей вне отрезка 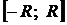(соответственно, 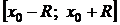), ряд расходится. На границах интервала сходимости, т. е. в точках 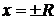(соответственно, в точках 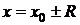) ряд может как сходиться, так и расходиться. Число 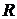называется радиусом сходимости степенного ряда.

В частности, при 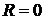областью сходимости ряда является одна точка 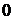(соответственно, 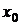), а при 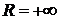областью сходимости является вся числовая прямая (такой ряд называется еще всюду сходящимся).

Интервал сходимости, как правило, определяется с помощью признака Даламбера или признака Коши, примененных к знакоположительным рядам 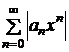или 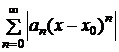, составленным из абсолютных величин членов исходных степенных ряд.

Для вычисления радиуса сходимости 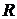степенного ряда применяются также формулы:

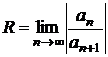и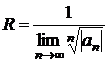

в тех случаях, когда указанные пределы существуют.

Пример. Найти область сходимости ряда .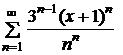

◄ Применяя непосредственно признак Коши к ряду, составленному из абсолютных величин членов исходного ряда, получаем

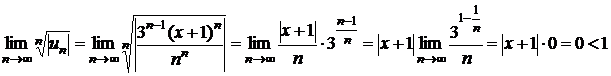для всех 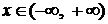. Следовательно, ряд сходится абсолютно в каждой точке числовой прямой 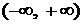(ряд всюду сходящийся). ►

Пример. Найти область сходимости ряда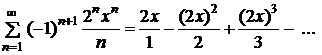

◄ Применяя непосредственно признак Даламбера к ряду, составленному из абсолютных величин членов исходного ряда, получаем

.

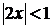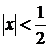
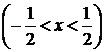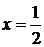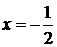Ряд сходится (абсолютно), если , т. е. если . Исследуем сходимость ряда на концах этого интервала, т. е. в точках и . При 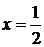получаем сходящийся (условно) ряд 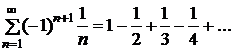, а при 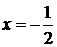― расходящийся гармонический 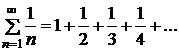Таким образом, область сходимости исходного ряда ― промежуток . ►

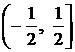Пример. Найти радиус сходимости ряда, рассмотренного в предыдущем примере.

◄ Для вычисления радиуса сходимости используем формулу, получающуюся на основе признака Даламбера. Учитывая, что коэффициенты ряда задаются формулой 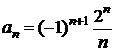, имеем

= .

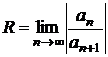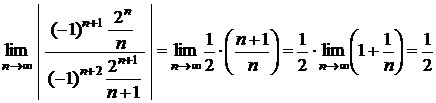Таким образом, ряд абсолютно сходится в интервале 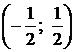. На границах этого интервала исследование проведено в предыдущем примере. Используя результаты этого исследования, получаем ту же самую область сходимости исходного ряда: . ►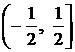