Интервал и радиус сходимости
Рассмотрим функцию 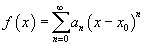 . Ее областью определения является множество тех значений x, при которых ряд сходится. Область определения такой функции называется интервалом сходимости.
. Ее областью определения является множество тех значений x, при которых ряд сходится. Область определения такой функции называется интервалом сходимости.
Если интервал сходимости представляется в виде 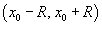 , где R > 0, то величина R называетсярадиусом сходимости. Сходимость ряда в конечных точках интервала проверяется отдельно.
, где R > 0, то величина R называетсярадиусом сходимости. Сходимость ряда в конечных точках интервала проверяется отдельно.
Радиус сходимости можно вычислить, воспользовавшись радикальным признаком Коши, по формуле
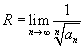
или на основе признака Даламбера:
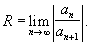
КОШИ - АДАМАРА ТЕОРЕМА
пусть задан степенной ряд
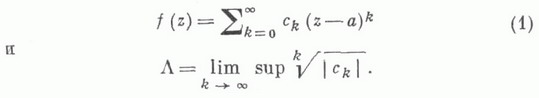
Если 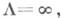 то ряд (1) сходится только в точке z=a; если
то ряд (1) сходится только в точке z=a; если 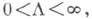 то ряд (1) абсолютно сходится в круге
то ряд (1) абсолютно сходится в круге 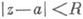 радиуса
радиуса

и расходится вне этого круга при 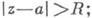 если
если 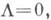 то ряд (1) абсолютно сходится при всех
то ряд (1) абсолютно сходится при всех  Содержание К. - А. т. выражается, таким образом, формулой Коши - Адамара (2), к-рую при этом следует понимать в расширенном смысле, включая равенства
Содержание К. - А. т. выражается, таким образом, формулой Коши - Адамара (2), к-рую при этом следует понимать в расширенном смысле, включая равенства 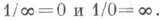 Иначе говоря, содержание К.- А. т. состоит в том, что внутренность множества точек (абсолютной) сходимости ряда (1) есть круг
Иначе говоря, содержание К.- А. т. состоит в том, что внутренность множества точек (абсолютной) сходимости ряда (1) есть круг 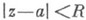 радиуса (2). В случае действительного степенного ряда (1) формула (2) определяет радиус интервала сходимости
радиуса (2). В случае действительного степенного ряда (1) формула (2) определяет радиус интервала сходимости 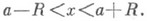 В основном К.- А. т. была высказана О. Коши (A. Cauchy) в его лекциях [1], опубликованных в 1821, полную ясность в формулировку и доказательство внес Ж. Адамар [2]. Для степенных рядов
В основном К.- А. т. была высказана О. Коши (A. Cauchy) в его лекциях [1], опубликованных в 1821, полную ясность в формулировку и доказательство внес Ж. Адамар [2]. Для степенных рядов
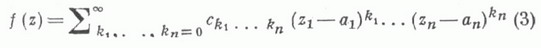
но n комплексным переменным  обобщением формулы Коши - Адамара является следующее соотношение:
обобщением формулы Коши - Адамара является следующее соотношение:
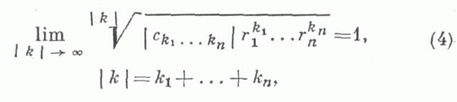
к-рому удовлетворяют сопряженные радиусы сходимости r1 . . . , rn ряда (3) (см. Круг сходимости). Записав соотношение (4) в виде  получают уравнение, определяющее границу нек-рой логарифмически выпуклой кратно круговой области с центром а, к-рая и является внутренностью множества точек абсолютной сходимости ряда (3) при n>1.
получают уравнение, определяющее границу нек-рой логарифмически выпуклой кратно круговой области с центром а, к-рая и является внутренностью множества точек абсолютной сходимости ряда (3) при n>1.
Свойства степенных рядов
Степенной ряд (1.2) представляет собой функцию  , определенную в интервале сходимости , т. е.
, определенную в интервале сходимости , т. е.
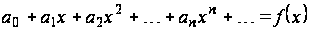 .
.
Приведем несколько свойств функции .
Свойство 1. Функция является непрерывной на любом отрезке 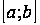 , принадлежащем интервалу сходимости.
, принадлежащем интервалу сходимости.
Свойство 2. Функция дифференцируема на интервале , и ее производная 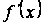 может быть найдена почленным дифференцированием ряда (1.2), т. е.
может быть найдена почленным дифференцированием ряда (1.2), т. е.
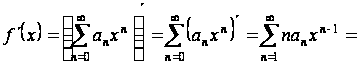
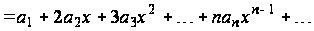 ,
,
для всех  .
.
Свойство 3. Неопределенный интеграл от функции для всех может быть получен почленным интегрированием ряда (1.2), т. е.
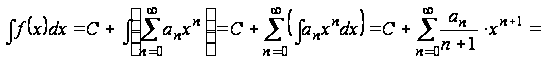
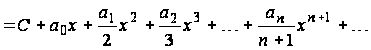
для всех .
Следует отметить, что при почленном дифференцировании и интегрировании степенного ряда его радиус сходимости R не меняется, однако его сходимость на концах интервала может измениться.
Приведенные свойства справедливы также и для степенных рядов (1.1).
Пример 2.1. Рассмотрим степенной ряд
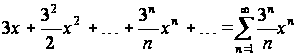 .
.
Область сходимости этого ряда, как показано в примере 1.1, есть промежуток .
Почленно продифференцируем этот ряд:
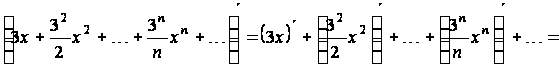
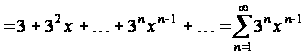 .(2.1)
.(2.1)
По свойству 2 интервал сходимости полученного степенного ряда (2.1) есть интервал .
Исследуем поведение этого ряда на концах интервала сходимости, т. е. при и при .
При степенной ряд (2.1) превращается в числовой ряд
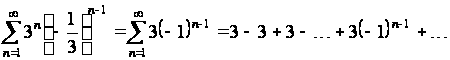 .
.
Этот числовой ряд расходится, так как не выполняется необходимый признак сходимости 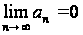 :
: 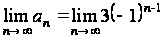 , который не существует.
, который не существует.
При степенной ряд (2.1) превращается в числовой ряд
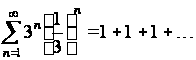 ,
,
который также расходится, так как не выполняется необходимый признак сходимости.
Следовательно, область сходимости степенного ряда, полученного при почленном дифференцировании исходного степенного ряда, изменилась и совпадает с интервалом .
