Уравнения первого порядка с разделяющимися переменными

Дифференциальное уравнение 1-го порядка

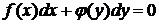(5.5)

является уравнением с разделенными переменными. Общий интеграл этого уравнения имеет вид

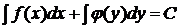. (5.6)

Уравнения, которые могут быть приведены к виду (5.5), называются уравнениями с разделяющимися переменными.

При разделении переменных в уравнении с разделяющимися переменными следует придерживаться следующего алгоритма:

· заменить в уравнении производную 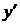на отношение дифференциалов 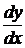(если это необходимо);

· умножить левую и правую части уравнения на ;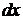

· применяя допустимые арифметические и алгебраические операции (группировку слагаемых, умножение и/или деление обеих частей уравнения на определенные выражения и др.), привести уравнение к виду (5.5), в котором обе переменные находятся при «своих» дифференциалах.

В тех случаях, когда затруднительно идентифицировать уравнение как уравнение с разделяющимися переменными, следует провести попытку такого разделения и, если это оказывается невозможным, сделать вывод, что оно с неразделяющимися переменными.

Пример. Решить уравнение .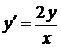

◄ Заменяем 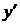на 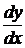: 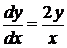; умножаем уравнение на 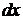: 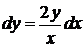; делим полученное уравнение на (тем самым присоединяем переменную к «своему» дифференциалу 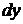): 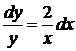– уравнение с разделенными переменными; интегрируем последнее уравнение: 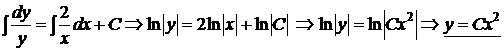– общее решение уравнения (при интегрировании для упрощения получения явного задания искомой функции произвольная постоянная С была записана в виде 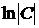, что допустимо, т. к. 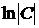(при 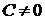) также представляет собой произвольную постоянную, принимающую любые значения от 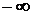до 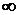). Семейство интегральных кривых 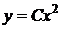при 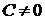представляет собой параболы с вершиной в начале координат, а при 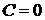– прямую . ►

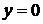Замечание. У дифференциальных уравнений могут существовать частные решения, которые не могут быть получены из его общего решения ни при каких значениях произвольных постоянных. При разделении переменных это достаточно часто возникает при делении уравнения на выражение, которое может обращаться в нуль.

Пример. Решить уравнение .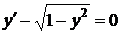

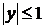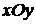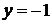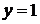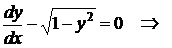
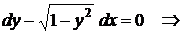
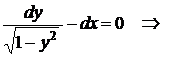
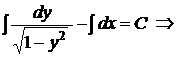
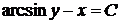
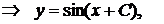
◄ Это уравнение задано лишь при , т. е. на полосе плоскости , заключенной между прямыми и (включая и точки границы). 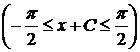– общее решение уравнения. Кроме того, при разделении переменных было проведено деление уравнения на 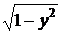, что можно делать только если это выражение не равно нулю. Однако 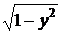обращается в нуль при 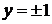. Непосредственной подстановкой можно убедиться в том, что 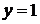и 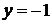являются еще двумя частными решениями уравнения, причем эти решения не получаются из общего ни при каких значениях произвольной постоянной . ►

Пример. Найти частное решение уравнения 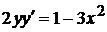, удовлетворяющее начальному условию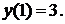

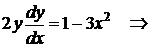
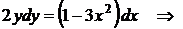
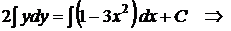
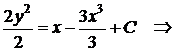
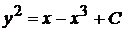◄ – общее решение уравнения. Подставив начальное условие 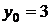при 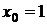в общее решение, получаем уравнение относительно 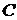: 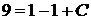. Из последнего уравнения имеем 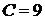. Следовательно, искомое частное решение имеет вид: 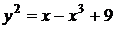(в виде неявной функции от ). ►