Решение задач контрольной работы

Задача 1

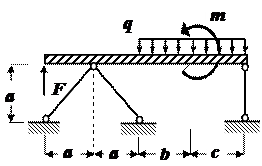
Абсолютно жесткий брус прикреплен к трем стержням при помощи шарниров (рис.7).Требуется:

1.Определить усилия в стержнях.

2.Считая, что все стержни круглого поперечного сечения, из условия прочности

при растяжении - сжатии подобрать диаметры этих стержней. Принять

допускаемое нормальное напряжение на сжатие [ s_с] = 100МПа, а на

растяжение - [ s_р] = 160МПа. Полученные по расчету диаметры стержней

округлить до четных или оканчивающихся на пять чисел (в миллиметрах).

3.Проверить прочность стержней.

Исходные данные:

a=2, 4 м; b=2 м; c=3 м;

m=32 кНм; F=30 кН; q=10 кН/м;

[ s_р] = 160МПа=160 ;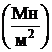

[ s_с] = 100МПа=100 .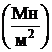

Рис.7

Решение

Определение усилий в стержнях

Для определения усилий в стержнях разрежем стержни и в местах разрезов приложим неизвестные пока усилия, предполагая, что они вызывают растяжение (рис.8). После этого составляем три уравнения равновесия:

Сумма проекций всех сил на горизонтальную ось x

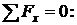- N₁·sin 45⁰ + N₂·sin 45⁰=0; N₁ = N₂.

Сумма моментов всех сил относительно точки B

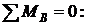- F·2, 4 - q·5· (5/2+2, 4) - m- N₃ · (2+3+2, 4) =0;

- 30·2, 4 - 10·5· (4, 9) -32- N₃ · (7, 4) =0;

- 349 - N₃ ·7, 4=0;

N₃ = 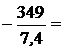- 47,162 кН = - 47, 2 кН; N₃ = - 47, 2 кН.

Сумма моментов всех сил относительно точки D

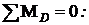- F· (2, 4+2, 4+2+3) + N₁·cos 45⁰ · (2, 4+2+3) +N₂·cos 45⁰ · (2, 4+2+3) +

+q·5·5/2 - m=0;

- 30·9, 8 +2N₁·cos 45⁰ · (7, 4) + 10·12, 5 -32=0;

N₁·10, 465- 201 =0;

N₁ = 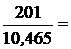19, 2069 кН = 19, 2 кН; N₁ = N₂ = 19, 2 кН.

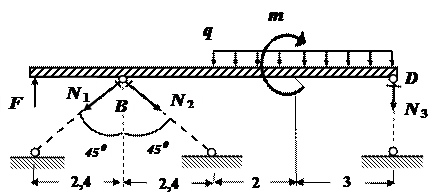
Рис.8

Проверяем правильность вычисления опорных реакций (сумма проекций всех сил на вертикальную ось z должна быть равна 0)

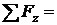F - N₁·cos 45⁰ - N₂·cos 45⁰ – q·5– N₃ = 30– 2·19, 2·0,707– 10·5–(- 47, 2 )=

= 77, 2 – 77, 15=0, 05=0.

Из полученных результатов видим, что первый и второй стержни испытывают растяжение, а третий – сжатие.

Подбор сечений стержней из условия прочности по методу допускаемых напряжений при растяжении-сжатии

Условие прочности при растяжении или сжатии по нормальным напряжениям по методу допускаемых напряжений имеет вид:

s 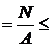[s]. (1)

В этой формуле: s -истинное или рабочее нормальное напряжение;

N-продольная сила в стержне; A-площадь поперечного сечения этого стержня; [s ] - допускаемое нормальное напряжение.

Условие прочности позволяет выполнить три вида расчета:

1.Проектный расчет. По заданной нагрузке определяют продольную силу N и из

Условия прочности находят величину требуемой площади поперечного сечения

.

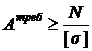2.Определение допускаемой нагрузки. По известной площади и допускаемому

напряжению определяют наибольшую величину допускаемой нагрузки

N .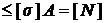

3.Проверочный расчет. По известным значениям N, A, [s] проверяют

выполнение условия прочности.

Переходим к определению размеров поперечных сечений стержней.

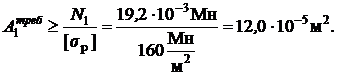
Но, с другой стороны, 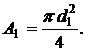Приравнивая 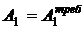, получаем

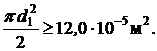
Откуда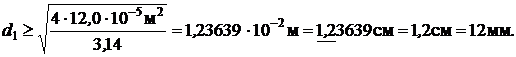

Принимаем d₁ = d₂ = 1,2 см.

Для третьего стержня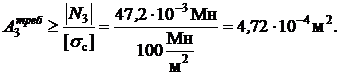

Приравнивая 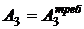, получаем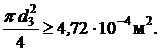

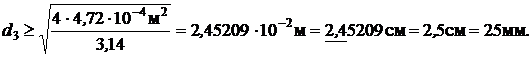
Принимаем d₃ = 2,5 см.

Проверка прочности стержней

Фактическая площадь поперечного сечения первого и второго стержней

,

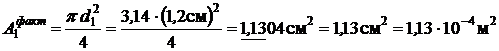тогда рабочее нормальное напряжение

.

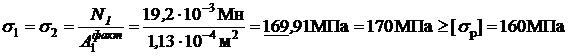Из полученного результата устанавливаем, что стержни перегружены. Определяем величину перегрузки

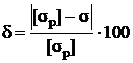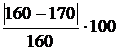% = % = 6,55 % > 5 % .

Замечание. По методу расчета по допускаемым напряжениям возможна

перегрузка стержней в пределах 5 %.

Увеличиваем диаметры первого и второго стержней d₁ = d₂ = 1,4 см.

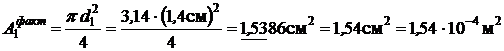, тогда рабочее нормальное напряжение

.

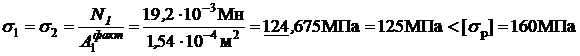Условие прочности выполняется.

Окончательно принимаем d₁ = d₂ = 1,4 см.

Фактическая площадь поперечного сечения третьего стержня

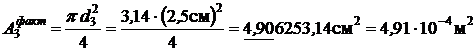, тогда рабочее нормальное напряжение

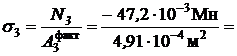- 96, 130МПа= - 96, 1МПа.

│s₃│= 96, 1МПа < [ s_с] = 100МПа.

Условие прочности выполняется. Окончательно принимаем d₃ = 2, 5 см.

Задача 2

Для заданного поперечного сечения, состоящего из прокатных профилей (рис.9), требуется:

1.Определить положение центра тяжести. Построить централь-

ные оси.

2.Найти величины осевых и центробежного моментов инерции

относительно центральных осей.

3. Определить направление главных центральных осей.

4. Найти величины осевых моментов инерции относительно

главных центральных осей.

5.Вычертить сечение в масштабе на миллиметровке формата А4

и указать на нем все размеры в числах и все оси.

Рис.9

Исходные данные: пластина - 200 ´ 20; равнобокий уголок - 160´160´12.

Решение

Будем считать, что пластина - фигура I, а равнополочный уголок -фи-гура II. Используя справочные таблицы, выписываем данные для каждой фигуры.

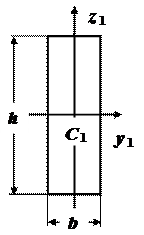Фигура I- пластина 200´20

b=20 мм =2см;h=200 мм =20 см;

A₁=b h= 2∙20см²=40 см²;

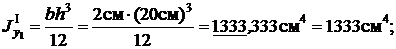
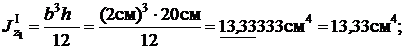
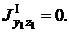
Фигура II - равнополочный уголок 160´160´12

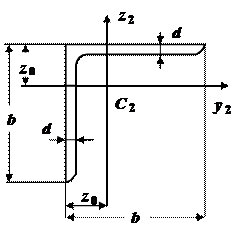b=160 мм =16см;

d=12мм =1, 2 см;

A₂=37, 4 см²;

z₀=4, 39см;

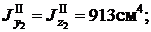
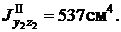
Здесь и в дальнейшем A_1, A₂ - соответственно площади первой и второй фигур, A - площадь составной фигуры (общая площадь). Верхние индексы I , II у моментов инерции соответствуют номерам фигур, их отсутствие означает, что определяется момент инерции всего сечения. Например, 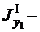момент инерции первой фигуры относительно оси y₁; 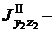центробежный момент инерции второй фигуры относительно осей y₂, z₂.

Замечание. В справочных таблицах значения центробежного момента инерции

уголка приводятся без учета знака. Знак центробежного момента

инерции можно выбрать в соответствии с рис.10.

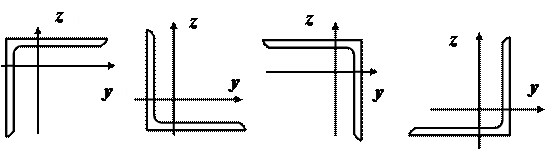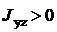
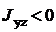
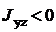
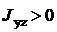
Рис.10

Используя приведенные выше справочные данные, вычерчиваем сечение в масштабе с указанием всех осей и необходимых размеров в сантиметрах (рис.11). На рис.11 в рамках показаны размеры, взятые из справочных данных, остальные получены в ходе расчета.