Знакопеременные ряды. Знакочередующиеся ряды. Признак Лейбница.

Ряды.

§1. Числовые ряды.

1. Основные понятия. Примеры.

Определение:Пусть {a_n} – числовая последовательность. Выражение a₁+a₂+…+a₃+…= 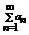называется числовым рядом. Числа а₁, а₂, …- члены ряда, причем a_n – общий член ряда. Сумма S_n=a₁+a₂+…+a₃= 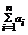называется n-ой частичной суммой данного ряда (сумма первых n членов ряда).

Определение:Если существует конечный предел последовательности {S_n} равный S, то ряд называется сходящимся, а число S – его суммой. .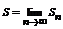

Если же такого предела не существует, либо он равен 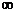, то ряд называется расходящимся.

Предложение:Ряд 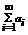- сходится , 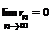(последовательность остатков 0).

Доказательство.Из равенства 1 можно представить r_n=S-S_n, тогда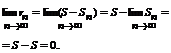

2. Простейшие свойства числовых рядов.

1.Перестановка, отбрасывание или добавление конечного числа членов ряда не влияет на его сходимость или расходимость.

2.Пусть 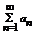ряд и ряд 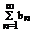- сходится, тогда сумма этих рядов 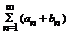тоже сходится.

Доказательство. 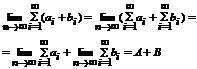- предел существует.

1.Если ряд 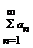- сходится, то и ряд 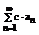-сходится, где c - некоторое число. Что всякая линейная комбинация сходящихся рядов есть сходящийся ряд.

§2. Необходимые условия сходимости числового ряда. Гармонический ряд.

Теорема 1 (необходимый признак сходимости). Если ряд 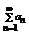- сходится, то общий член ряда → 0 ( ).

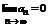Доказательство.Между частичными суммами существует следующая связь: S_n=S_n-1+a_n, и поэтому .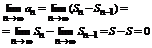

Следствие: (достаточный признак расходимости). Если 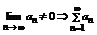, то ряд расходится.

Пример1. 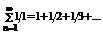-гармонический ряд. 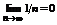→ ряд расходится.

§3. Признаки сходимости рядов с неотрицательными членами.

Общий вид: , .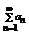

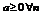Теорема 1 (предельный признак сравнения). Пусть 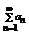и 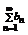с положительными членами. Если существует 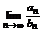, которы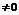й и 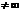, тогда ряды 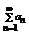и 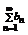сходятся или расходятся одновременно.

Доказательство. Обозначим 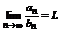; 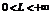. Согласно определению обозначим все члены последовательности { 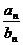} начиная с некоторого номера находящегося сколь угодно близко к L, т.е. 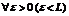существует номер 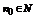такой, что .

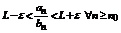Умножим все части неравенства на b_n (b_n>0), получим следующее:

.

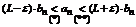1.Пусть сходится ряд 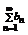, тогда сходится 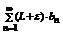и тогда согласно теореме 3 ввиду неравенства (**) сходится ряд .

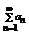2.Пусть сходится ряд 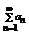, тогда согласно теореме 3 ввиду неравенства (**) сходится ряд 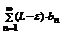из чего следует сходимость .

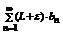Аналогично доказывается случай расходимости.

Замечание.Применяя признак сходимости чаще всего сравнивают с 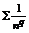и .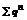

Теорема 2 (признак сравнения). Пусть имеется два ряда 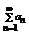и и 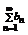существует номер n₀ 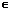N такой, что выполняется следующее неравенство 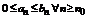, тогда:

1. если ряд 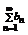- сходится 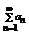- сходится.

2. если ряд 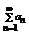- расходится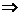 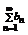- расходится.

Доказательство. Можно считать, что члены второго ряда 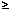членам первого ряда уже начиная с первого номера (иначе можно рассматривать остатки ряда; их сходимость и расходимость равносильна сходимости или расходимости рядов). Считаем, что неравенства 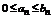выполняется для 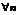, тогда аналогичное неравенство выполняется и для {S_n}, т.е. .

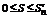1. Пусть 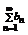- сходится, тогда последовательность { 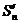}- ограничена, значит ограничена и последовательность {S_n} 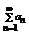- сходится.

2. Пусть 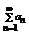- расходится. Это означает, что неограниченна его последовательность частичных сумм S_n = { 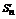} – неограниченна, значит расходится .

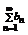§4.Признаки Д’ Аламбера и Коши сходимости знакоположительных числовых рядов.

Теорема 1 (признак Д’Аламбера). Пусть 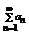, 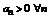и пусть существует 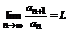, тогда:

1. Если L<1 - сходится.

2. Если L>1 - расходится.

Доказательство. Согласно определению интеграла для 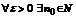такой, что .

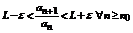1.Пусть L<1, тогда можно выбрать 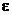такое, что 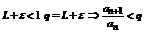, так как a_n>0 a_n+1<qa_n 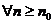в частности .

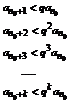Рассмотрим ряд, членами которого являются правые части 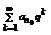- геометрическая прогрессия со знаменателем 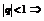сходится, значит согласно теореме 3 сходится ряд

и из левых частей 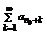(но этот ряд равен исходному) = 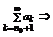что сходится .

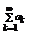2. Пусть L>1 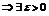, такой, что 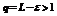согласно левой части неравенства получаем, что .

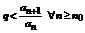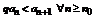
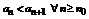, т.к. q>1.

Это означает, что последовательность {a_n} – не убывающая по крайней мере начиная с номера n₀ тем самым 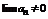тогда не выполняется необходимый признак сходимости и значит ряд расходится.

Теорема 2 (признак Коши). Пусть 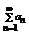, 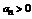и пусть предел 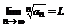тогда:

1. Если L<1 - сходится.

2. Если L>1 - расходится.

Доказательство. Согласно определению предела для 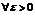существует 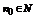такой, что .

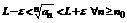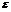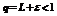
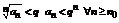
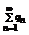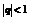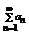1. Пусть L<1; можно подобрать так, чтобы - сходится (прогрессия с ), то - сходится по теореме 3.

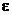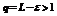
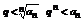
2. Пусть L>1; можно подобрать так, чтобы 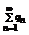- расходится, тогда согласно теореме 3 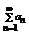- расходится.

§5. Интегральный признак сравнения.

Теорема 2 (интегральный признак сходимости). Пусть 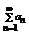- ряд с положительными членами и существует функция f(x) > 0 непрерывная и определенная на интервале [1; + ),

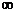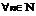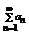такая что f(n)=a_n, . Ряд сходится , когда сходится .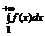

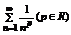- ряд Дирихле: при p>1 – ряд сходится;

при p 1 – ряд расходится.

Доказательство.Для произвольного действительного числа x найдутся целые числа k такие, что 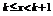. Так как f(x) монотонно убывает: 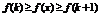. Перейдем к интегралам в неравенстве: .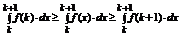

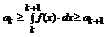Просуммируем эти неравенства при всех k=1, .., n.

.

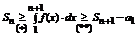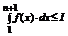b)Пусть сходится , где I – число, тогда . Это означает по неравенству (**), что S_n+1-a₁ 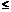I, т.е. 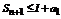последовательность частичных сумм ограничена.

c)Пусть 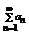- сходится, тогда {S_n} – ограничена. Согласно неравенству (*), тогда и последовательность интегралов { 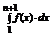} – ограничена и значит она сходится при 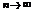, т.е. сходится несобственный интеграл 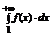- сходится.

Пусть ряд 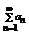- расходится, т.е. расходится последовательность {S_n} – (неограниченно возрастает). Тогда S_n+1-a₁ – также неограниченно возрастает. В силу неравенства (**) последовательность { }–

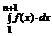d)неограниченно возрастает. Тогда 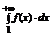- расходится.

e)Если расходится интеграл 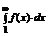по (*) что 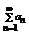- расходится.

q<1 – сход.

q>1- расход.

§6,7. Знакопеременные ряды. Знакочередующиеся ряды. Признак Лейбница.

6. Знакопеременные ряды. Абсолютная и условная сходимость.

Ряд называется знакопеременным, если среди его членов имеются как положительные, так и отрицательные.

Теорема1. Если знакопеременный ряд 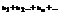таков, что ряд, составленный из абсолютных величин его членов 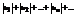сходится, то и данный знакопеременный ряд также сходится.

Знакопеременный ряд называется абсолютно сходящимся, если сходится ряд, составленный из абсолютных величин его членов. Если же знакопеременный ряд сходится, а ряд, составленный из абсолютных величин его членов расходится, то данный ряд называется условно или не абсолютно сходящимся рядом.

Знакопеременными называются ряды, которые содержат как положительные, так и отрицательные члены, со сколь угодно большими номерами.

Частным случаем таких рядов являются знакочередующие, т.е. ряды, в которых любые 2 соседних члена имеют разные знаки.

Знакочередующие ряды удобно представить в виде 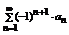(*), где 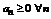(в случае если a₁>0).

Теорема 1 (признак Лейбница). Пусть знакочередующийся ряд (*) удовлетворяет следующим условиям:

1. 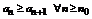(начиная с номера n₀ монотонно убывает).

2. ,

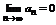тогда данный ряд сходится, причем для 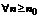справедливо следующая оценка остатка .

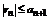Доказательство. Можно считать, что условие 1 выполняется для всех n. Рассмотрим частичную сумму S_2n. Сгруппируем слагаемые следующим образом:

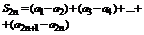
каждая разность в скобках неотрицательная. Т.е. последовательность 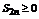и S_2n возрастающая последовательность.

С другой стороны последовательность S_2n представима следующим образом 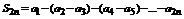, опять в скобках все разности неотрицательны .

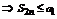Тем самым последовательность {S_2n} ограничена и значит она сходится.

Обозначим через .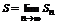

Рассмотрим 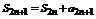, тогда .

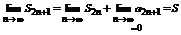Таким образом все частичные суммы имеют предел S. Из полученных оценок 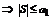, поэтому n-ый частичный остаток .

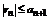Пример. .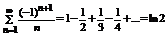

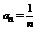- убывающая последовательность 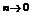, значит условие признака Лейбница выполняется - ряд сходится.

§8. Признаки условной сходимости. Особенности условно сходящихся рядов.

Теорема Дирихле (признак Дирихле). Если частичная сумма a_n ряда 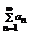образует ограниченную последовательность, кроме того последовательность {b_n} монотонно убывает и 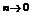, то ряд 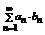- сходится.

Признак Лейбница является частным случаем данной теоремы.

Теорема Абеля.Пусть ряд 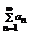- сходится и {b_n} монотонно убывающая последовательность состоящая из положительных членов. Тогда ряд 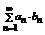- сходится.

Теорема Римана.Пусть ряд 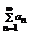-сходится условно и его сумма: 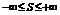, тогда существует такая перестановка членов данного ряда после которой исходный ряд сходится и его сумма = S.

§9. Функциональные ряды.

Пусть u₁(x), u₂(x)…- последовательность функций, определенных на множестве X. 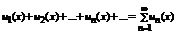- называется функциональным рядом.

Для всякого числа 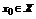ряд 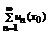- обычный числовой ряд.

Если данный числовой ряд сходится, то x₀ – точка сходимости данного функционального ряда. Множество всех точек сходимости называется областью сходимости функционального ряда (D). .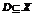

Функция 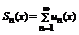называется n-ой частичной суммой данного ряда, а функция 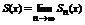называется суммой данного ряда. Функция 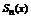определена на множестве D.

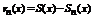- n-ый частичный остаток данного ряда. Переходя к пределу видим, что .

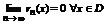Сходимость о которой идет речь выше называется поточечной сходимостью.

Если сходящийся ряд 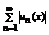в какой-то точке x_n, то такая сходимость называется абсолютной.

Множество D₁ точек x₀ в которых ряд сходится абсолютно называется областью абсолютной сходимости ряда .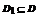

2. Равномерная сходимость функциональных рядов.

Функциональный ряд 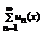называется равномерно сходящимся в области D к 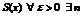(не зависящее от x),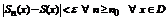

Дадим параллельную формулировку поточечной сходимости.

Ряд 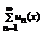называется поточечно сходящимся к сумме 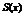в области D, если 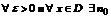(вообще говоря зависящее от x), такой что .

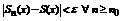3. Признак Вейерштрасса.

Теорема. Если для функционального ряда 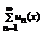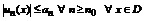, причем ряд 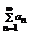- сходится. Тогда функциональный ряд 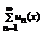сходится равномерно на множестве D.

Доказательство. Обозначим через 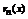n-ый частичный остаток 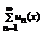, а через 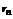n-ый частичный остаток 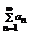. Так как ряд 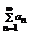- сходится 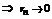, т.е. 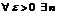(не зависящее от x) такой что .

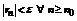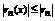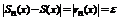
В силу условия теоремы ; 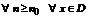. Ряд сходится равномерно на D.

Числовой ряд 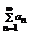в формулировке теоремы называется мажоритарным рядом для данного функционального мажорантой. Функциональный ряд для которого существует мажоранта называется мажорируемым.

Достаточным признаком равномерной сходимости функционального ряда являются мажоранты, которые сходятся.

Данный признак достаточный, но не необходимый. Это значит, что если мажоранты не существуют, то нельзя говорить о том, что ряд сходится.

4. Свойства равномерно сходящихся рядов.

Теорема 1 (о непрерывности суммы равномерно сходящихся рядов). Если на множестве D функциональный ряд 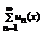с непрерывными членами сходится равномерно, то его сумма S(x) непрерывна на этом множестве.

Доказательство. Согласно определению равномерной сходимости для 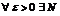(не зависящий от x) такой что 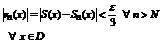. Пусть 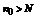, для 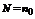условие выполняется.

Функция 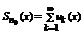непрерывна на множестве D. Как конечная сумма непрерывных функций. Для любого 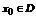и для выбранного 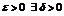такое что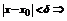 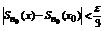(определение непрерывности ).

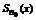Тогда для выбранного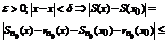

.

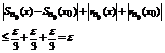Теорема 2 (о почленном интегрировании равномерно сходящихся рядов).

Если функциональный ряд 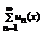сходится к функции S(x) равномерно на отрезке 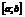, то его можно почленно интегрировать по любому отрезку 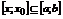и справедливо равенству 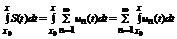, причем последний ряд сходится равномерно на отрезке .

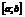Доказательство. В силу равномерной сходимости данного функционального ряда для 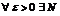(не зависит от x), такой что .

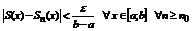Тогда 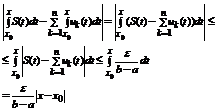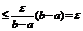. Справедливо 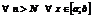. А это означает, что ряд 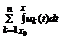- сходится равномерно на 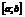к .

Теорема 3 (о почленном дифференцировании равномерно сходящихся рядов). Если ряд 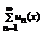сходится на отрезке 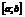к сумме S(x).Члены ряда 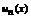дифференцированы на отрезке и ряд сумма 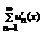- сходится на 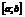- равномерно, то данный ряд так же сходится на 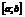равномерно, причем его сумма дифференцирована на 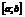и выполняется равенство . (*)

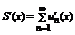§10. Степенные ряды.

Функциональный ряд вида 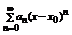, где 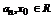называется степенным рядом по степеням .

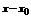С помощью замены 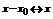получим ряд 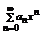. Исходный получается обратной заменой из данного.

Теорема Абеля (о сходимости степенных рядов). Для всякого степенного ряда 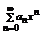существует неотрицательное число R ( возможно 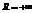) такое, что ряд сходится абсолютно при 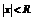- сходится равномерно при 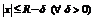- расходится при .

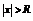Доказательство. Ряд заведомо сходится при x=0. Если других точек сходимости нету, то очевидно число R=0.

Предположим, что 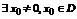(область сходимости). Так как ряд 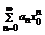- сходится, то согласно признаку сходимости общий член ряда 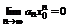. Это означает, что последовательность 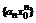, будучи сходящейся, ограничена, т.е. 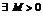, так что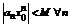 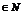пусть x такой, что 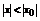. 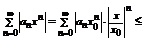(в силу оценок полученных выше) 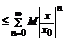- сходится как сумма геометрической прогрессии ( ).

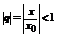Получаем, что данный степенной ряд сходится абсолютно при любом x, таком, что .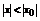

Отсюда видно, что в качестве R можно взять 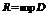(D- область сходимости).

При 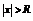- ряд расходится, поскольку мы оказываемся за пределами границы области сходимости.

Если 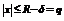, то 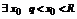. Тогда получаем, что 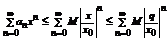- мажоритарный ряд для 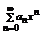, который сходится , так как это геометрическая прогрессия ( 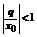). Значит данный ряд сходится равномерно в указанной области согласно признаку Вейерштрасса.

Замечание. Число R, о котором идет речь в условии теоремы, называется радиусом сходимости данного функционального ряда. Интервал (-R; R), внутри которого ряд сходится абсолютно называется интегралом сходимости.

Степенной ряд по степеням ( 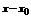) то он имеет интервал сходимости ( ).

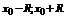Кроме интервала сходимости в область сходимости могут входить края.

2. Свойства степенных рядов.

1. Сумма степенного ряда непрерывна на интервале сходимости (причем ).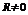

Доказательство. Пусть 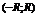- интервал сходимости: 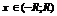. . 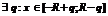По теореме Абеля ряд сходится равномерно на 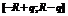и, значит, сумма его непрерывна во всех точках данного отрезка, в частности, в точке x.

2. Операция почленного дифференцирования и интегрирования по любому отрезку от 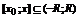степенного ряда не имеет его радиуса сходимости.

Доказательство. Предположим, что существует предел 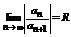. Рассмотрим ряд полученный почленным дифференцированием ряда 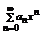, получим .

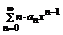Пусть радиус сходимости .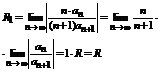

Рассмотрим ряд полученный почленным интегрированием x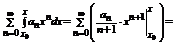

.

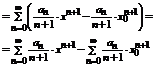Второй ряд из этих двух является числовым и он сходится, поскольку 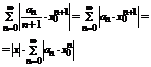сходится, т.к. 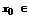интервалу сходимости.

Вычислим 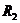(радиус сходимости первого ряда). .

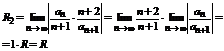3. Степенной ряд можно любое количество раз дифференцировать на отрезке сходимости .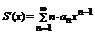

Доказательство. Вытекает из теоремы о почленном дифференцирование функциональных рядов.

4. Степенной ряд можно почленно интегрировать любое количество раз по любому отрезку .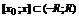

§11. Ряды Тейлора.

Пусть функция 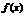- бесконечно дифференцирован в окрестности точки 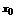(т.е существует производная). Поставим этой функции в соответствие ряд 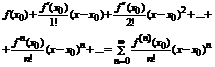. Данный ряд называется рядом Тейлора функции 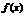в окрестности точки 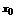. В частном случае, когда 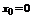, получаем 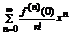- ряд Маклорена функции .

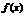Замечание 1. Ряд Тейлора является степенным рядом, следовательно имеет радиус сходимости и интервал сходимости. Однако сумма ряда необязательно совпадает с функцией 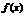. За пределами интервала сходимости сумма проста не существует.

Если же сумма ряд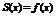а на 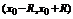то говорят, что функция 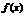разложима в ряд Тейлора в окрестности точки .

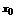Замечание 2. Частичные суммы ряда Тейлора представляются следующими многочленами: 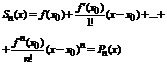, которые есть ничто иное, как многочлены Тейлора (обозначим их через P(x)).

Существует формула Тейлора, которая имеет вид: 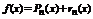, где 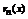-остаток формулы Тейлора. Для остатка были получены следующие оценки: 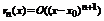- оценка остатка в форме Пеана, а также 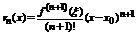, где точка расположена между x₀ и x. Оценка остатка формулы Тейлора в форме Лагранжа.

Обозначим через 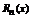- остаток ряда Тейлора. Вообще говоря 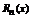и 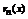не одно и тоже. Действительно 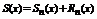и формула Тейлора 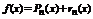одно и тоже.

Но если 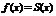, т.е. функция 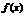- разложима в ряд Тейлора, то остаток ряда Тейлора совпадает с остатком формулы Тейлора.

Это позволяет для оценки остатка ряда Тейлора использовать оценки остатка формулы Тейлора.

Теорема 1. Для того, чтобы бесконечно дифференцированная функция 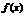разложилась в ряд Тейлора в окрестности точки .

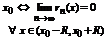Доказательство. Мы уже отметили, что разложение означает 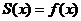, а это в свою очередь .

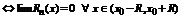Теорема 2 (достаточный признак разложения в ряд Тейлора). Если 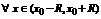, все производные функции 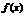ограничены одной и той же константой M (это свойство называется равномерной ограниченностью на данном интервале), то ряд Тейлора функции 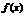- сходится к функции .

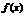Доказательство. Воспользовавшись теоремой 1 покажем, что 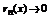. Применим формулу Лагранжа, для оценки остатка формулы Тейлора. Имеем:

.

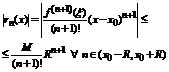Числовой ряд 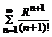- сходится по признаку Д’Аламбера, то согласно необходимому признаку сходимости. Предел .

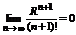Таким образом и 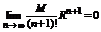. Следовательно ввиду оценки и .

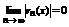Теорема 3 Если степенной ряд по степеням 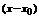- сходится к функции 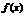в окрестности точки 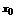, то он является рядом Тейлора для данной функции.

Доказательство. Пусть 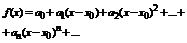Согласно свойствам степенной ряд можно любое количество раз почленно дифференцировать в окрестности точки .

.

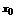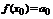После дифференцирования: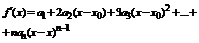

Из полученных равенств находим, что .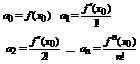

Т.е. коэффициенты совпадают с коэффициентом ряда Тейлора.

……………

………………

.

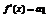
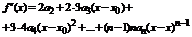
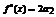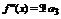
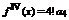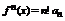§12. Разложение функций в ряд Тейлора (Маклорена).

1) .

.

(*)

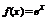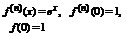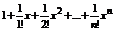Покажем, что ряд сходится к e.

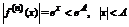
Полученный ряд (*) сходится к функции 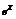для любого x.

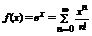- расходится на R.

2)

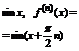
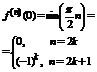
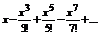
3)

.

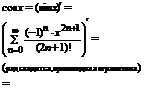
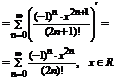4)

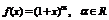
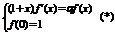- дифференциальное уравнение, с начальным условием.

Задача Коши.

5)

.

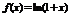
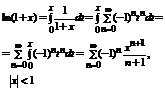Сходится на .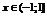

15. Приложения степенных рядов. Приближенное вычисление значений ф-ций. Вычисление сумм числовых рядов.

Приближенное в