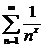Знакочередующиеся числовые ряды

Ряд вида 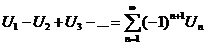, где U_n>0 называется знакочередующимся числовым рядом. U_n – общий член. Положительный и отрицательный член ряда чередуются по знакам через один.

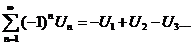
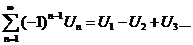
Для знакочередующихся числовых рядов справедлива теорема Лейбница – достаточное условие сходимости такого ряда.

Теорема Лейбница:Дан знакочередующийся числовой ряд 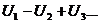- члены которого:

1) Убывают ( )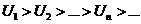

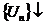2) 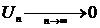, т.е

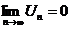
ряд сходится и его сумма S удовлетворяет неравенству 0<S< U₁

Доказательство:

Рассмотрим четную частичную сумму ряда:

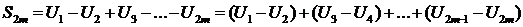
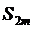>0

перепишем подругому

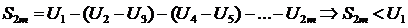
Последовательность четных частичных сумм возрастает и ограничена сверху U₁, поэтому существует 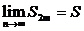( по теореме о предельном переходе в неравенствах: 0<S< U₁)

Рассмотрим нечетную частичную сумму ряда

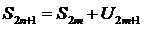
перейдём к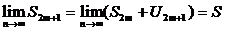

Конец доказательства.

Следствие: т.к 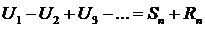, где 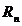- n-ый остаток ряда,т.е с помощью теоремы Лейбница появляется возможность оценить погрешность (остаток 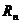) возникающую при замене суммы ряда его частичной суммой.

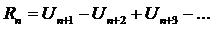Т.к n остаток ряда - тоже является рядом из чередующихся чисел, то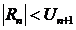

Определение:Числовые ряды, в которых члены произвольны по знакам называется знакопеременными рядами. Знакочередующийся ряд является частным случаем знакопеременного ряда. Для знакопеременных рядов очень трудно установить сходимость, но можно рассмотреть ряд из модулей (отбросить знаки). Такой ряд будет знакоположительным.

Для знакопеременного ряда справедлива следующая теорема:

Пусть 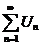- знакопеременный числовой ряд. Ряд из 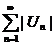- соответствующий ему ряд из модулей.

Если 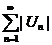сходится то и 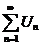тоже сходится.

Доказательство: 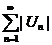обозначим 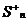- сумма положительных слагаемых

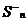сумма отрицательных слагаемых.

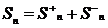n частичная сумма ряда из модулей.

Т.к ряд 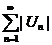сходящийся, то 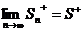и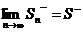

Рассмотрим n частичную сумму ряда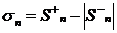

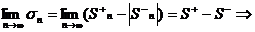
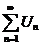- сходится.

Определение:Дан знакопеременный числовой ряд 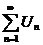Если ряд из модулей 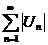-сходится, то знакопеременный ряд называется абсолютно сходящимся. Если 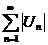-расходится, а ряд 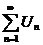все таки сходится, то знакопеременный ряд называется условно сходящимся.

При исследовании знакопеременного ряда на абсолютную сходящимость нужно проверить следующие условия:

1) 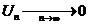, если не стремится то ряд расходится и исследование окончено.

2)На абсолютную сходимость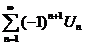

заменим рядом из модулей. К ряду из модулей можно применять I и II признаки сравнения, признаки Даламбера, радикальный признак Коши и интегральный признак Коши.

Если ряд из модулей сходится, то исходный ряд сходится абсолютно. Исследование можно закончить.

3) На условную сходимость по теореме Лейбница: 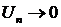и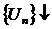

Примеры:

1)

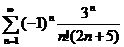
2)

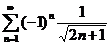
3)

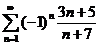
Функциональные ряды

Определени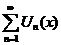е: , где 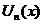- функции переменной х называется функциональным рядом.

При некоторых значениях х функциональный ряд сходится, при других значениях х – расходится.

Определение:Множество значений переменной х, при которых функциональный ряд 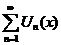- сходится, называется областью сходимости функционального ряда. Задача нахождения области сходимости функционального ряда является весьма трудной, хотя для некоторых рядов область сходимости найти легко.

Пример:

1)

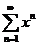
2)