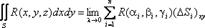Криволинейный интеграл 2 рода

Пусть задана некоторая линия γ. Найти работу, которая совершит переменная сила F( x, y ) при перемещении некоторой точки из положения А в положении В по линии γ.

Разобьем линию на бесконечно малые участки точками М1, М2, … , тогда работа силы на всей линии равна сумме работ на каждом участке

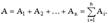
Так как отрезки разбиения бесконечно малы, то их условно можно считать прямолинейными отрезками. Кроме того, будем считать, что в пределах каждой ячейки сила не меняется, и она в пределах ячейки определяется вектором в некоторой точке Ci внутри этой ячейки. Работу внутри каждой ячейки приближенно заменим на элементарную работу силы (скалярное произведение силы на вектор перемещения)

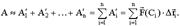
Данная сумма называется криволинейной интегральной суммой второго рода.

Предел криволинейной суммы второго рода, при условии стремления к нулю всех участков разбиения, называется криволинейным интегралом второго рода, если он существует, не зависит от разбиения линии и от выбора точек внутри каждой ячейки

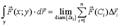
Если вектор силы задан своими координатами, которые являются функциями координат точки

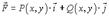
то, воспользовавшись формулой скалярного произведения в координатной форме, получим криволинейный интеграл второго рода в координатной форме: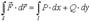

Формула Грина

Теорема Грина устанавливает связь между криволинейным интегралом по замкнутому контуру C и двойным интегралом по области D, ограниченной этим контуром. Фактически, эта теорема является частным случаем более общей теоремы Стокса. Теорема названа в честь английского математика Джорджа Грина.

Пусть C — положительно ориентированная кусочно-гладкая замкнутая кривая на плоскости, а D — область, ограниченная кривой C. Если функции P = P(x,y), Q = Q(x,y) определены в области D и имеют непрерывные частные производные 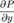, , 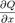то

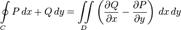
На символе интеграла часто рисуют окружность, чтобы подчеркнуть, что кривая C замкнута.

Поверхностный интеграл 1 рода

Предел поверхностной интегральной суммы первого рода при безграничном ростре числа областей дробления σ1, σ2, … , σ n и стремления к нулю длины контуров всех областей дробления называется поверхностным интегралом первого рода

.

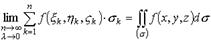
Нормаль к поверхности

Одной из основных характеристик поверхности является её нормаль — единичный вектор, перпендикулярный касательной плоскости в заданной точке:

.

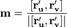
Знак нормали зависит от выбора координат.

Поверхностный интеграл 2 рода

Если при стремлении к нулю шага разбиения поверхности S интегральные суммы, составленные как суммы произведений значений некоторой функции на площадь частичной поверхности, имеют конечный предел, то этот предел называется поверхностным интегралом второго рода.