Экономико–математические методы и модели
Уральский филиал
федерального государственного бюджетного образовательного учреждения высшего профессионального образования
«Российский Экономический Университет им. Г.В. Плеханова»
Старший преподаватель Перминова Е.А.
Экономико–математические методы и модели
Екатеринбург
Методическое руководство предназначено для проведения занятий и самостоятельной работы по курсу «Линейное программирование» для студентов дневного обучения. Работа содержит краткие теоретические сведения по изучаемым разделам, примеры решения задач, задания для курсовой или лабораторных работ студентов.
Руководство состоит из двух основных частей: «линейное программирование» и «транспортная задача линейного программирования». В первом разделе рассматриваются следующие темы: обзор основных задач линейного программирования, методы решения задач: геометрический, симплекс-метод, метод искусственного базиса. Также рассмотрены вопросы построения и решения двойственных задач ЛП.
Раздел «транспортная задача линейного программирования» содержит краткие сведения по теории оптимизации грузовых перевозок и назначений в распределительных задачах. При работе с данным руководством предполагается использование специально разработанных программных средств (ПС). Индивидуальные задания для студентов содержат задачи, требующие как умения решать задачи «вручную», так и с использованием указанных ПС. Руководство составлено в соответствии с учебным планом и предназначено для проведения занятий со студентами всех специальностей дневного обучения.
Автор:
Перминова Е.А., ст. преподаватель,
Рецензент:
Скачков П.П., доцент кафедры «Высшая математика», УрГУПС
© РоссийскаяЭкономическая Академия им. Г.В. Плеханова», 2011
СОДЕРЖАНИЕ
1. ОСНОВНЫЕ ПОНЯТИЯ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ.. 5
Правила перехода от одной модели к другой. 7
1.1 Переход от стандартной модели ЗЛП к канонической. 7
1.2. Переход от канонической модели задачи ЛП к стандартной. 7
1.3. Переход от основной модели задачи ЛП к канонической. 8
2. Геометрическая иллюстрация решения задач ЛП.. 9
3. Двойственность в задачах линейного программирования 11
3.1. Построение двойственных моделей. 11
3.2. Теоремы двойственности. 13
3.3. Экономическая интерпретация переменных двойственной задачи. 14
4. Симплекс-метод в задачах ЛП.. 16
4.1. Основные положения симплекс-метода. 16
4.2. Правило преобразования симплекс-таблиц. 17
4.3. Геометрическая интерпретация симплекс-метода. 20
5. Метод искусственного базиса.. 21
5.1. Постановка задачи. 21
5.2. Теоремы метода. 21
5.3. Примеры решения задач. 22
Индивидуальные задания.. 28
6. ТРАНСПОРТНАЯ ЗАДАЧА ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ.. 31
6.1. Транспортная задача линейного программирования. 31
6.1.1. Постановка задачи. 31
6.1.2. Математическая модель. 31
6.2. Методы определения начального опорного плана. 32
6.2.1. Метод северо-западного угла. 32
6.2.2. Метод наименьшей стоимости. 33
6.2.3. Метод двойного предпочтения. 34
6.3. Метод потенциалов. 35
6.4. Построение цикла и определение величины
перераспределения груза. 35
6.5. Открытая транспортная задача. 38
6.6. Проблема вырожденного плана задачи. 39
ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ.. 40
7. ЗАДАЧА ОБ ОПТИМАЛЬНОМ НАЗНАЧЕНИИ.. 41
7.1. Постановка задачи. 41
7.2. Математическая модель. 41
7.3. Решение задачи о назначениях венгерским методом.. 42
7.4. Решение задачи максимизации. 44
ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ.. 45
БИБЛИОГРАФИЧЕСКИЙ СПИСОК.. 46
Методы оптимизации
Оптимизационные задачи бывают двух типов: задачи минимизации и задачи максимизации, т.е. отыскание наименьшего или наибольшего значения целевой функции f(X) на допустимом множестве. Оптимизационная задача, в которой целевая функция является линейной, множество допустимых значений задается системой линейных уравнений или линейных неравенств, называется задачей линейного программирования.
При этом система линейных уравнений или линейных неравенств называется системой ограничений задачи линейного программирования.
ОСНОВНЫЕ ПОНЯТИЯ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
Линейное программирование (ЛП) - это раздел математики о методах исследования и поиска наибольших и наименьших значений некоторой линейной функции, причем ограничения задачи тоже линейны. Математические модели задач линейного программирования (ЗЛП) различаются между собой по виду ограничений.
Определение 1. Математическую модель ЗЛП будем называть стандартной, если ограничения в ней представлены в виде линейных неравенств, а целевая функция минимизируется или максимизируется.
Например, пусть в модели два неизвестных: х1, х2. Надо найти среди решений системы неравенств такие, которые дают целевой функции наибольшее (наименьшее) значение. Такая модель имеет вид:
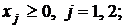
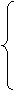
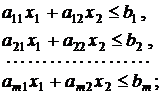 (1.1)
(1.1)
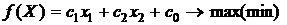 (1.2),
(1.2),
где 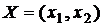 - искомое решение системы.
- искомое решение системы.
Здесь, система линейных неравенств, определяющая допустимое множество решений задачи (1.1), называется системой ограничений задачи линейного программирования, а линейная функция 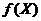 называется целевой функцией или критерием оптимальности.
называется целевой функцией или критерием оптимальности.
Определение 2. Математическая модель ЗЛП называется основной, если ограничения в ней представлены в виде уравнений при условии неотрицательности переменных. Такая модель имеет вид:
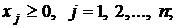
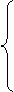
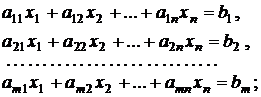 (1.3)
(1.3)
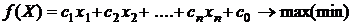 (1.4),
(1.4),
где 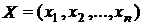 - искомое решение системы.
- искомое решение системы.
Система уравнений (1.3) обычно имеет конечное множество решений. Целевая функция f(х) - линейная, поэтому частные производные постоянны, а это значит, что внутри области решений системы (1.3) экстремальных точек нет. Если целевая функция имеет оптимальное решение, то оно достигается в точках границ области.
Таким образом, в линейном программировании исследователя интересуют вершины многоугольника решений системы (1.3). Отсюда возникает вопрос: какой вид должна иметь модель ЛП, чтобы координаты вершин многоугольника решений могли быть легко получены? Рассмотрим другие модели задач линейного программирования.
Определение 3. Математическая модель называется канонической, если ее система ограничений представлена в виде системы m линейно независимых уравнений (ранг системы r = m), в системе выделен единичный базис, свободные переменные и целевая функция выражена через свободные переменные.
Запишем каноническуюмодель ЗЛП:
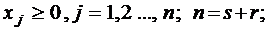
|
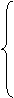
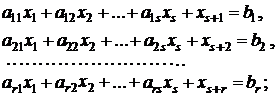 (1.5)
(1.5) 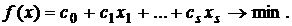
Определение 4. Будем называть переменные, входящие в одно из уравнений системы с коэффициентом один и отсутствующие в других уравнениях, базисными неизвестными, а все другие – свободными.
В нашей модели переменные x1,...,хs _ – свободные, и, если их принять равными нулю, то из системы (1.5) легко получить значения базисных переменных xs+1, xs+2,..., xs+r .
Определение 5. Решение системы называется базисным, если в нем свободные переменные равны нулю,и оно имеет вид:
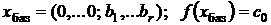 .
.
Базисное решение является угловой точкой множества решений системы (1.5), или, можно сказать, определяет вершину многоугольника решений модели. Среди таких решений находится и то, при котором целевая функция принимает оптимальное значение.
Определение 6.Базисное решение называется опорным, если оно допустимо, то есть все правые части уравнений (неравенств) положительны 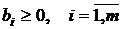 .
.
Теорема 1.Базисное опорное решение в канонической модели является оптимальным, если все коэффициенты в целевой функции не положительны, то есть 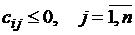 .
.
Теоремы двойственности
Теорема 1. Если X – любое опорное решение исходной задачи, а Y – любое опорное решение соответствующей ей двойственной задачи, то 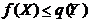 .
.
Теорема 2. Если одна из взаимно двойственных задач имеет оптимальное решение, то и другая тоже имеет оптимальное решение, причем оптимальные значения целевых функций равны между собой 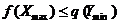 .
.
Теорема 3.Если одна из взаимодвойственных моделей не имеет оптимального решения (например, целевая функция неограниченна), то и другая не имеет допустимых решений, то есть система ограничений в ней – несовместна.
Теорема 4. Пусть одна из взаимно двойственных задач имеет оптимальное решение. Тогда для неизвестных и ограничений выполняются следующие условия:
1) если координата хjоптимальногоплана исходной модели строго положительна, то соответствующее ограничение выполняется при подстановке в него координат оптимального решения, как уравнение;
2) если при подстановке Xопт вкакое-либо ограничениеисходной задачи оно выполняется как строгое неравенство, то соответствующая ему переменная уi равна нулю.
Теорема 5.Для того, чтобы два допустимых решения Х* и Y* пары двойственных задач были оптимальными решениями, необходимо и достаточно, чтобы они удовлетворяли системе уравнений:
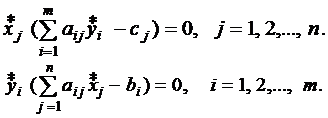
Зная оптимальное решение одной из двойственных задач, можно, используя теоремы двойственности, найти оптимальное решение другой. Рассмотрим пример.
Пример. Вернемся к задаче, решение которой мы получили в п.2. Построим для заданной модели двойственную и решим ее с помощью теорем двойственности:
 12x1+4x2 ≤ 300, y1 ≥ 0,
12x1+4x2 ≤ 300, y1 ≥ 0,
4x1+4x2 ≤ 120, y2 ≥ 0,
3x1+12x2 ≤ 252, y3 ≥ 0,
x1 ≥ 0,12y1 +4y2+3y3 ≥ 30,
x2 ≥ 0,4y1+4y2+12y3 ≥ 40,
f(x) =30x1 + 40 x2 → max. q(y) =300 y1 + 120y2 + 252y3 →min.
Двойственная модель задача ЛП построена по правилу, изложенному ранее.
Нам известно, что исходная задача имеет оптимальное решение:
Xmax = (12, 18), fmax= f (Xmax) = 1080.
Воспользуемся первой теоремой двойственности. Двойственная модель тоже имеет оптимальное решение, причем оптимальное значение целевой функции q(y)тоже равно 1080, то есть q(Ymin) = 1080.
Далее, будем использовать теорему 4. Начнем с 1-ой части:
x1 = 12 > 0 Þ 12y1+4y2+3y3 = 30,
x2 = 18 > 0 Þ 4y1+4y2+12y3 = 40.
Подставим оптимальное решение xmax в ограничения задачи:
144 + 72 = 216 < 300 Þ у1 = 0,
48 + 72 = 120 = 120 Þ у2 > 0,
36 + 216 = 252 = 252 Þ у3 > 0.
Получим систему уравнений для определения оптимального решения двойственной модели:
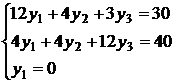
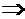
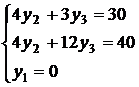
Получим: 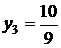 ,
, 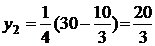 ,
, 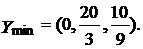
Проверим расчет: 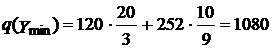 .
.
 Задача решена.
Задача решена.
Симплекс-метод в задачах ЛП
Симплексный метод позволяет, отправляясь от известного опорного решения задачи, за конечное число шагов получить оптимальное решение. Каждый из шагов состоит в нахождении нового решения, которому соответствует меньшее значение целевой функции, чем значение этой функции при предыдущем решении. Процесс повторяется до тех пор, пока не будет получен оптимальный план.
Метод искусственного базиса
Постановка задачи
Для того чтобы привести задачу ЛП к канонической форме, необходимо предварительно найти некоторое начальное опорное решение этой задачи. Мы можем ввести в модель искусственные переменные, которые должны быть базисными и неотрицательными. Исключение искусственных переменных производится с помощью преобразования симплекс-таблиц. Процесс решения содержит два этапа: переход от основной модели к канонической ® решение задачи.
Пусть исходная система имеет следующий вид:
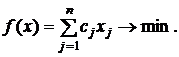
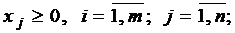
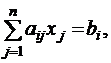
(5.1)
Без ограничения общности можно считать, что 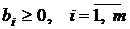 . Для отыскания опорного решения строим вспомогательную задачу:
. Для отыскания опорного решения строим вспомогательную задачу:
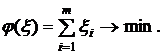
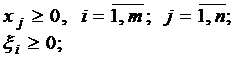
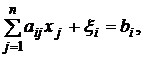
(5.2)
Свойства вспомогательной задачи:
1. Вспомогательная задача всегда имеет оптимальное решение.
2. Вектор 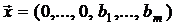 является опорным решением задачи (5.2).
является опорным решением задачи (5.2).
Таким образом, принимая этот вектор за начальное опорное решение, вспомогательную задачу можно решить симплекс-методом.
Пусть 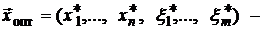 оптимальное опорное решение задачи (5.2). Тогда, если
оптимальное опорное решение задачи (5.2). Тогда, если 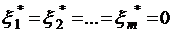 , то
, то 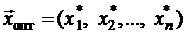 - опорное решение исходной задачи (5.1). Если же среди чисел
- опорное решение исходной задачи (5.1). Если же среди чисел 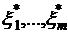 есть положительные, то задача (5.1) не имеет допустимых решений. Таким образом, всегда можно либо найти опорное решение исходной задачи (5.1), либо установить ее неразрешимость.
есть положительные, то задача (5.1) не имеет допустимых решений. Таким образом, всегда можно либо найти опорное решение исходной задачи (5.1), либо установить ее неразрешимость.
Теоремы метода
Теорема 1. Для того, чтобы исходная система имела опорные решения, необходимо и достаточно, чтобы 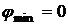 (минимальное значение функции во вспомогательной задаче равно нулю).
(минимальное значение функции во вспомогательной задаче равно нулю).
Теорема 2. Если исходная система имеет опорные решения, то существует равносильная ей каноническая система, получаемая из завершающей таблицы вспомогательной задачи.
Замечания к теоремам
Замечание 1. Если φmin вспомогательной задачи не равна 0, то исходная задача не обладает опорным решением (несовместна).
Замечание 2. Если при решении вспомогательной задачи:
а) в завершающей симплекс-таблице все вспомогательные переменные вышли из базиса, тогда, полагая их равными 0, получаем каноническую задачу для исходной;
б) вспомогательная переменная в некотором уравнении осталась в базисе, тогда необходимо левую часть ограничения приравнять к 0 и путем преобразований выделить базисную переменную для данного уравнения.
Следовательно, из завершающей таблицы вспомогательной задачи получим каноническую форму задачи (5.1).
Примеры решения задач
Пример 1. Пусть дана задача линейного программирования:
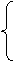 5х1 + 5х2 – x3 = 5,
5х1 + 5х2 – x3 = 5,
10х2 - х4 = 5,
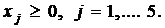 х1 + х2 + x5 = 5.
х1 + х2 + x5 = 5.
f(x) = 5x2→max.
Первое и второе уравнения не имеют базисных переменных, в третьем уравнении такой переменной является х5. Чтобы получить каноническую модель задачи, вводим две базисные переменные:
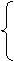 5х1 + 5х2 – x3 + x 1 = 5,
5х1 + 5х2 – x3 + x 1 = 5,
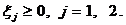 10х2 - х4 + x 2 = 5,
10х2 - х4 + x 2 = 5,
х1 + х2 + x5 = 5,
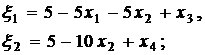
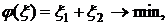 где
где
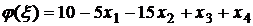 , или
, или 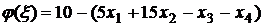 .
.
Используя систему уравнений с базисными переменными и функцию цели 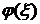 , составляем исходную симплекс-таблицу.
, составляем исходную симплекс-таблицу.
Таблица 5.1
| Базис | В | х1 | х2 | х3 | х4 | х5 | ξ1 | ξ2 |
 ξ1 ξ1 | -1 | |||||||
| ξ2 | -1 | |||||||
| х5 | ||||||||
| φ(x) | -1 | -1 |
Будем вводить в базис переменную х1 и выводить ξ1. Преобразуем первую строку так, чтобы в клетке разрешающего элемента была единица. Для этого разделим все элементы первой строки на 5. Получим новую первую строку для следующей таблицы (табл. 5.2).
Далее необходимо получить в столбце под переменной x1 нули. Перепишем вторую строку без изменений, так как в ней на нужном месте уже стоит нуль. Остальные нули в столбце получим, умножив получившуюся первую строку на (-1) и (-5) и сложив ее поэлементно с третьей и четвертой строкой таблицы 5.1. Получаем новую симплекс-таблицу 5.2.
Таблица 5.2
| Базис | В | х1 | х2 | х3 | х4 | х5 | ξ1 | ξ2 |
| х1 | -1/5 | 1/5 | ||||||
 ξ2 ξ2 | -1 | |||||||
| х5 | 1/5 | -1/5 | ||||||
| φ(x) | -1 | -1 |
Аналогично вводим в базис переменную х2вместо ξ2. Для этого делим вторую строку таблицы 5.2 на 10, и результат записываем во вторую строку следующей таблицы (табл.5.3). Затем умножаем получившуюся вторую разрешающую строку на (-1) и (-10) и складываем ее поэлементно с первой и четвертой строкой таблицы 5.2. Новая симплекс-таблица имеет вид:
Таблица 5.3
| Базис | В | х1 | х2 | х3 | х4 | х5 | ξ1 | ξ2 |
| х1 | 1/2 | -1/5 | 1/10 | 1/5 | -1/10 | |||
| х2 | 1/2 | -1/10 | 1/10 | |||||
| х5 | 1/5 | -1/5 | ||||||
| φ(x) | -1 | -1 |
По теореме 1 метода искусственного базиса данная система имеет оптимальный план ( 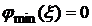 ), следовательно, по теореме 2 существует равносильная каноническая система, полученная из завершающей таблицы вспомогательной задачи.
), следовательно, по теореме 2 существует равносильная каноническая система, полученная из завершающей таблицы вспомогательной задачи.
Так как в завершающей симплекс-таблице вспомогательной задачи все вспомогательные переменные вышли из базиса, тогда, полагая их равными 0, получаем каноническую задачу для исходной задачи ЛП:
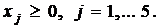
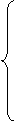
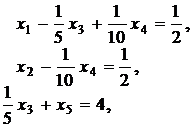
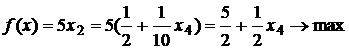 или
или 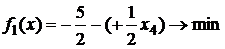
Составляем симплекс-таблицу по полученным данным:
Таблица 5.4
| Базис | В | х1 | х2 | х3 | х4 | х5 |
 х1 х1 | 1/2 | -1/5 | 1/10 | |||
| х2 | 1/2 | -1/10 | ||||
| х5 | 1/5 | |||||
| f1(x) | -5/2 | 1/2 |
Вводим в базис x4. Выполняя обычные преобразования симплекс-метода и результаты вычислений запишем в табл.5.5.
Таблица 5.5
| Базис | В | х1 | х2 | х3 | х4 | х5 |
| х4 | -2 | |||||
| х2 | -1/5 | |||||
 х5 х5 | 1/5 | |||||
| f1(x) | -5 | -5 |
Вводим в базис х3 . Получаем следующую таблицу 5.6.
Таблица 5.6
| Базис | В | х1 | х2 | х3 | х4 | х5 |
| х4 | ||||||
| х2 | ||||||
| х3 | ||||||
| f(x) | -25 | -5 | -5 |
Так как в индексной строке нет положительных элементов, следовательно, получили завершающую симплекс-таблицу, в которой содержится оптимальный план задачи.
Хопт = (0, 5, 20, 45, 0)
fmin(x) = -25 , тогда fmax(x) = 25.
Пример 2. Дана основная задача линейного программирования. При помощи элементарных преобразований матрицы коэффициентов системы ограничений, привести задачу к стандартному виду и решить ее геометрическим методом. Методом искусственного базиса получить каноническую задачу (или доказать несовместность этой системы). Решить полученную модель с помощью симплекс- таблиц (или доказать, что она не имеет оптимального плана).
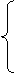
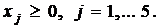
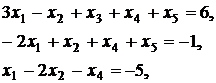
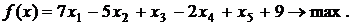
Запишем и преобразуем матрицу коэффициентов системы.

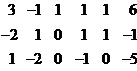 →
→ 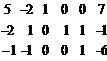 →
→ 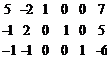
Получили систему ограничений с единичным базисом (х3; х4; х5):
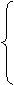
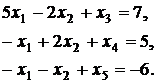
Отбрасывая базисные переменные, получим стандартную задачу ЛП: 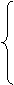
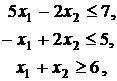
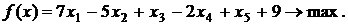
Выразим функцию цели через свободные неизвестные х1 и х2. Имеем:
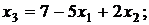
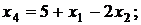
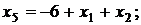
тогда 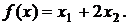
Решим задачу геометрическим способом, как показано в разделе 2. Область планов представляет собой треугольник АВС и функция цели достигает максимального и минимального значения в его вершинах:

Из рисунка видно, что точка В(3, 4) − точка максимума, тогда:
f(Xопт) = 3 + 2·4 = 11.
Для решения задачи симплекс-методом приведем систему ограничений к каноническому виду методом искусственного базиса. Заменив знаки в третьем ограничении, сделаем правые части уравнений неотрицательными:
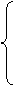 |
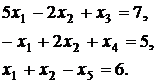
Очевидно, что в третьем уравнении нет базисной переменной. Используем метод искусственного базиса. Введем в это уравнение вспомогательную переменную ξ. Теперь решим вспомогательную задачу по минимизации функции 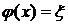 симплекс-методом.
симплекс-методом.
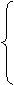
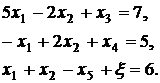
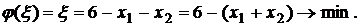
Занесем эту задачу в таблицу
Таблица 1
| Б | В | х1 | х2 | х3 | х4 | х5 | ξ |
| x3 | -2 | ||||||
| x4 | -1 | ||||||
| ξ | -1 | ||||||
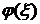 |
Введем в базис х2, тогда из базиса выйдет переменная х4. Пересчитывая таблицу, получим:
Таблица2
| Б | В | х1 | х2 | х3 | х4 | х5 | ξ |
| x3 | |||||||
| x2 | 2.5 | -0.5 | 0.5 | ||||
| ξ | 3.5 | 1.5 | -0.5 | -1 | |||
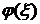 | 3.5 | 1.5 | -0.5 | -1 |
Введем в базис х1, тогда из базиса выйдет переменная ξ. Пересчитывая таблицу, получим:
Таблица 3
| Б | В | х1 | х2 | х3 | х4 | х5 | ξ |
| x3 | 8/3 | 7/3 | 8/3 | -8/3 | |||
| x2 | 11/3 | 1/3 | -1/3 | 1/3 | |||
| x1 | 7/3 | -1/3 | -2/3 | 2/3 | |||
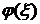 | -1 |
Данная таблица - завершающая таблица метода, она содержит оптимальный план вспомогательной задачи. Поскольку, 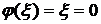 , то, отбрасывая последний столбец, получаем каноническую систему для исходной задачи.
, то, отбрасывая последний столбец, получаем каноническую систему для исходной задачи.
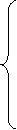
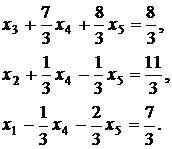
Выразим функцию цели через свободные переменные:
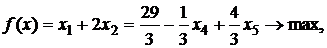
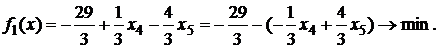
и решим исходную задачу симплекс-методом.
| Б | В | х1 | х2 | х3 | х4 | х5 |
| x3 | 8/3 | 7/3 | 8/3 | |||
| x2 | 11/3 | 1/3 | -1/3 | |||
| x1 | 7/3 | -1/3 | -2/3 | |||
| f1(X) | -29/3 | -1/3 | 4/3 |
Выполняя преобразования, получаем оптимальный план, доставляющий минимум функции цели f1(X) .
| Б | В | х1 | х2 | х3 | х4 | х5 |
| x5 | 0.375 | 0.875 | ||||
| x2 | 0.25 | 0.25 | ||||
| x1 | 0.125 | 0.625 | ||||
| f1(X) | -11 | -0.5 | -1.5 |
Получен оптимальный план. Запишем ответ
Хопт = (3; 4; 0; 0;1);
f1(Xопт) = -11 (min), тогда f1(Xопт) = 11 (max).
Индивидуальные задания
Задание 1
Предприятие выпускает два вида продукции А1 и А2, используя при этом три вида сырья S1, S2 и S3. Известны запасы сырья равные b1, b2 и b3 соответственно. Расход сырья вида Si на производство единицы продукции Aj равен ai,j. Доход от реализации единицы продукции Aj составляет cj условных единиц. Требуется составить такой план производства продукции, при котором доход будет максимальным.
Решить задачу графическим методом; составить каноническую модель данной задачи и решить ее симплекс-методом. Найти двойственные оценки цен на сырье, из решения симметричной двойственной задачи по теоремам двойственности.
| Вариант 1. | |||
| А1 | А2 | bi | |
| B1 | 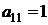 | 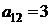 | |
| B2 | 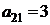 | 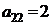 | |
| B3 | 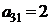 | 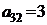 | |
| cj |
| Вариант 2. | |||
| А1 | А2 | bi | |
| B1 | 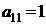 | 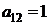 | |
| B2 | 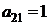 | 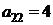 | |
| B3 | 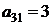 | 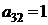 | |
| cj |
| Вариант 3. | |||
| А1 | А2 | bi | |
| B1 | 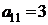 | 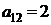 | |
| B2 | 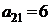 | 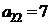 | |
| B3 | 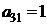 | 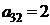 | |
| cj |
| Вариант 4. | |||
| А1 | А2 | bi | |
| B1 | 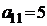 | 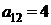 | |
| B2 | 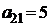 | 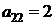 | |
| B3 | 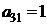 | 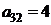 | |
| cj |
| Вариант 5. | |||
| А1 | А2 | bi | |
| B1 | 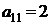 | 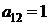 | |
| B2 | 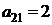 | 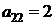 | |
| B3 | 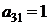 | 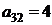 | |
| cj |
| Вариант 6. | |||
| А1 | А2 | bi | |
| B1 | 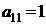 | 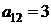 | |
| B2 | 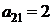 | 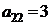 | |
| B3 | 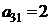 | 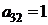 | |
| cj |
| Вариант 7. | |||
| А1 | А2 | bi | |
| B1 | 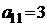 | 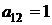 | |
| B2 | 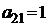 | 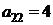 | |
| B3 | 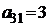 | 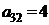 | |
| cj |
| Вариант 8. | |||
| А1 | А2 | bi | |
| B1 | 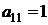 | 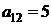 | |
| B2 | 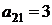 | 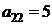 | |
| B3 | 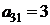 | 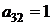 | |
| cj |
| Вариант 9. | |||
| А1 | А2 | bi | |
| B1 | 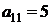 | 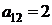 | |
| B2 | 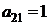 | 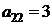 | |
| B3 | 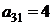 | 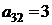 | |
| cj |
| Вариант 10. | |||
| А1 | А2 | bi | |
| B1 | 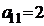 | 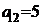 | |
| B2 |
