Векторы на плоскости и в трехмерном пространстве

Полагая, что понятия плоскости и трехмерного пространства известны читателю из школьного курса геометрии, обобщим, а в некоторых случаях уточним, начальные сведения о векторах.

Векторомназывается направленный отрезок 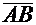с начальной точкой A и конечной точкой B, который можно перемещать параллельно самому себе. Обозначение: 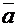или .

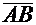Длиной (модулем, нормой) 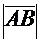вектора 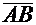называ­ется число, равное длине отрезка AB, изображающего вектор.

Векторы называются коллинеарными, если они лежат на одной прямой или на параллельных прямых, и компланарными, если их количество равно трем и они лежат в одной плоскости или на параллельных плоскостях.

Если точки начала и конца вектора совпадают, напри­мер, 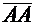то такой вектор называется нулевым вектором и обозначается: 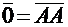. Длина нулевого вектора равна нулю, т.е. 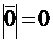. Поскольку направление нулевого вектора не определено, то его считают коллинеарным любому вектору.

Произведением вектора 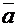на число λ называется век­тор: 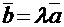имеющий длину 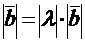и направление, совпадающее с напра­влением вектора 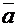если λ > 0, и противопо­ложное ему, если λ < 0.

Противоположным вектором вектору 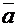называется произведение этого вектора на число (− 1), т.е. .

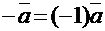Перенесем вектор параллельно самому себе таким образом, чтобы его начальная точка совпала с началом координат. Тогда можно ввести понятие координат вектора.

Координатами вектора называются координаты его конечной точки, если его начальная точка помещена в начало координат. При этом координатами вектора 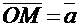на плоскости являются числа 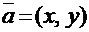, где M(x, y), а в трехмерном пространстве – соответственно – числа 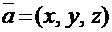, где M(x, y, z).

В соответствии с приведенными определениями не трудно показать, что суммой векторов 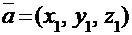и 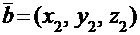будет вектор 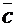с координатами: 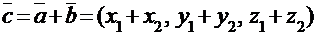, произведением вектора 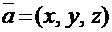на число l будет вектор 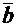с коор­динатами: .

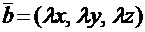Из тех же определений следует, что длина вектора равна квад­рат­ному корню из суммы квадратов его координат:

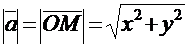или .

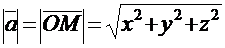соответственно, на плоскости и в трехмерном пространстве.

Скалярным произведением 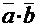двух векторов называется число (скаляр), равное произведению длин этих векторов на косинус угла j между ними, т.е.: 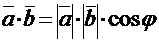. Скалярное произведение векторов можно выразить и через координаты этих векторов:

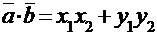или .

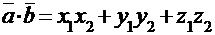соответственно, на плоскости и в трехмерном пространстве.

Если 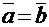, то очевидно угол между векторам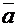и и 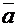будет равен нулю, следовательно:

,

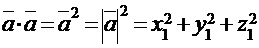т.е. скалярный квадрат вектора равен квадрату его длины.

Очевидно, что косинус угла между векторами будет определяться выражением:

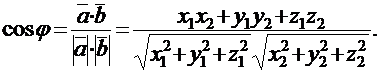
3.2. N-мерный вектор и векторное пространство

Определение. N-мерным вектором называется упорядочен­ная сово­купность n действительных чисел: 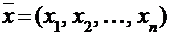а каждое число х_i называ­ется i-ой компонентой(координатой) вектора.

По аналогии с векторами на плоскости (двухмерными векторами) и в трехмерном пространстве (трехмерными векторами) можно сформулировать следующие пра­вила, которые следует рассматривать как аксиомы.

Два n-мерных вектора равнытогда и только тогда, когда равны их соответствующие компоненты, т.е. 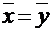, если 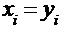для всех .

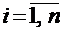Суммой двух n-мерных векторов называется n-мерный вектор, компоненты которого равны сумме соответствующих компо­нент слагаемых векторов, т.е. если 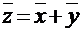то 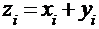для всех .

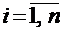Произведением n-мерного вектора на дейст­ви­тельное число называется n-мерный вектор, компоненты которого равны произ­ведению этого числа на соответствующие компоненты этого вектора, т.е. если 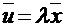, то 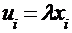для всех .

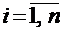Операции над векторами, установленные этими правилами, принято называть линейными операциями. Линейные операции над векторами должны удовлетворять целому ряду свойств, рассматривае­мых как аксиомы.

1. 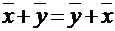- коммутативное свойство суммы.

2. 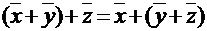- ассоциативное свойство суммы.

3. 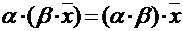- ассоциативное свойство относительно числового множителя.

4. 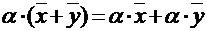- дистрибутивное свойство относительно суммы векторов.

5. 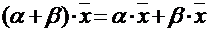- дистрибутивное свойство относительно суммы числовых множителей.

6. Существует нулевой вектор 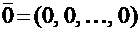такой, что 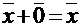для любого вектора 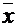, в этом – особая роль нулевого вектора.

7. Для любого вектора 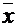существует противоположный вектор 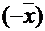такой, что .

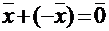8. Для любого вектора 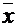справедливо 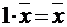, в этом – особая роль числового множителя 1.

Определение. Векторным (линейным) пространством называется множество векторов с действительными компонен­тами, в котором определены операции сложения векторов и умножения вектора на число, удовлетворяющие приведенным восьми аксиомам,

ПРИМЕР:Для заданной матрицы А размера mxnстроки этой матрицы можно рассматривать как множество n-мерных векторов.