Волны в трехмерном пространстве

Сферически симметричная задача

Сначала рассмотрим для однородного уравнения

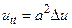, (2)

задачу, обладающую центральной симметрией относительно некоторой точки М₀. В качестве примера можно привести задачу о радиальных колебаниях газа. Итак, будем искать решения уравнения (2)

,

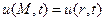где r – расстояние между точками М и М₀. В этом случае уравнение (2) после записи его в сферической системе координат можно свести к одномерному уравнению для функции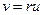

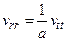(3)

Причем, если функция u(r,t) ограничена при 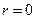, то функция 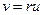при 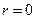обращается в нуль. В результате задача Коши для уравнения (2) с начальными условиями

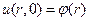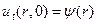и (4)

сводится к задаче о колебаниях полуограниченной струны 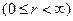с закрепленным концом в точке :

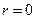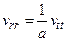
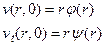(5)

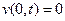
Эта задача была нами решена в §4 гл. II, поэтому, не умаляя общности, мы можем записать общее решение уравнения (3) в более удобном для нас виде

,

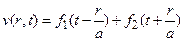где f₁ и f₂ – произвольные дважды дифференцируемые функции. Тогда для функции 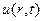будем иметь

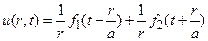(6)

Слагаемые в правой части (6) представляют собой частные решения уравнения (2)

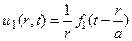и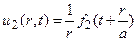

и являются сферическими волнами; 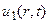есть расходящаяся сферическая волна, а 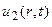– сходящаяся сферическая волна. В отличие от плоских волн, сферическая волна убывает обратно пропорционально расстоянию от центра.

Учитывая теперь нулевое граничное условие 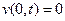, получим

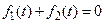или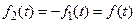

Тогда решение (6) примет вид

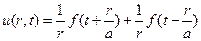(7)

и при 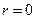, воспользовавшись формулой Лагранжа, можем записать

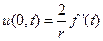(8)

Формула Пуассона

Теперь решим однородное волновое уравнение

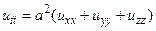(9)

с начальными условиями

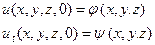(10)

Будем предполагать, что φ(x,y,z)непрерывна вместе со своими производными до третьего порядка, а ψ (x,y,z) – до второго порядка включительно во всем пространстве.

Покажем сначала, что интеграл

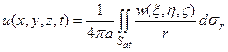, (11)

взятый по поверхности сферы 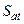радиуса 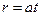с центром в точке M (x,y,z), является решением волнового уравнения (9), причем функция w(ξ,η,ζ) является произвольной. Координаты сферы 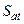могут быть выражены по формулам

, ,

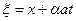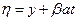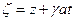
где α, β, γ – направляющие косинусы текущего радиуса сферы 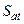, которые, как известно, могут быть записаны в виде

, , ,

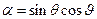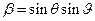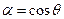где угол θ меняется от 0 до π и угол 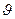от 0 до 2π. Когда точка (ξ,η,ζ) описывает сферу 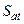, точка (α, β, γ) описывает сферу S₁ единичного радиуса с центром в начале координат, а между соответствующими элементами площади dσ_rи dσ₁ обеих сфер имеется соотношение

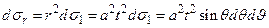
Тогда интеграл (11) приводится к виду

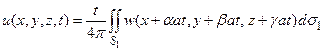(12)

Отсюда легко заметить, что функция 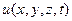имеет непрерывные производные до k-го порядка, если функция w (ξ,η,ζ) непрерывна вместе со своими производными до k-го порядка.

Из формулы (12) находим

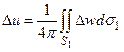
или, возвращаясь к первоначальной области интегрирования

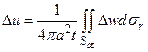(13)

Дифференцируя теперь выражение (12) по t, получим

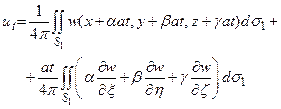(14)

Чтобы вычислить 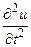, перепишем последнее выражение в виде

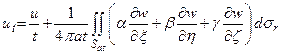
и, применив формулу Остроградского, получим

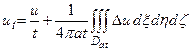
где D_at – шар радиуса 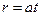с центром в точке M (x,y,z). Обозначая в этой формуле определенный интеграл через I, мы можем переписать её в виде

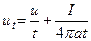
Дифференцируя это выражение по t, получим

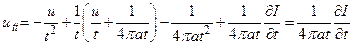(15)

Теперь убедимся, что

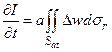(16)

Действительно, переходя в интеграле I к сферическим координатам 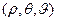с центом в точке M (x,y,z), имеем

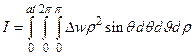
Теперь дифференцируя это выражение по t, получим

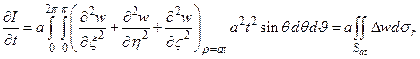
Сравнивая (13), (15) и (16) убеждаемся, что функция 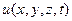, определяемая формулой (11), удовлетворяет волновому уравнению (9), какова бы ни была функция w(x,y,z), имеющая производные до второго порядка включительно.

Из формул (12) и (14) следует, что в этом виде функция u удовлетворяет начальным условиям

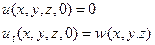(17)

Тогда, если функция u есть решение волнового уравнения (9) с начальными условиями (17), то можно убедиться, что функция

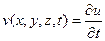
будет также решением уравнения (9), удовлетворяющим начальным условиям

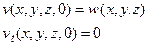(18)

Взяв теперь в качестве функции w(x,y,z) в начальных условиях (17) функцию 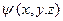, а в начальных условиях (18) функцию 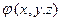и сложив построенные таким образом решения, мы получим решение уравнения (9), удовлетворяющее начальным условиям (10).

Таким образом, решение уравнения (9), удовлетворяющее начальным условиям (10), запишется в виде

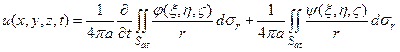(19)

Эта формула называется формулой Пуассона.