Многоканальная СМО с ожиданием

Пусть СМО имеет только несколько каналов (n≥1), на которые поступает пуассоновский поток заявок П_вх с интенсивностью 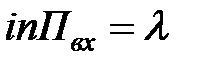. Поток обслуживания простейший и имеет интенсивность m. Заявка, поступившая на вход в момент, когда все каналы заняты обслуживанием не покидает систему, а становится в очередь и ожидает обслуживания. Далее предполагаем, что в данной системе нет ограничений на длину очереди и на время ожидания в очереди. Таким образом, длина очереди станет бесконечной, как и число состояний СМО.

Такая система представляет собой предельный случай СМО, при m®¥.

Если l>nm, т.е. среднее число заявок, поступивших в систему за единицу времени, больше среднего числа обслуживаемых всеми каналами заявок за то же время при непрерывно работающих каналах, то очевидно, что очередь неограниченно растёт. В этом случае предельный режим не устанавливается и предельных вероятностей состояний не существует.

Если l=nm, и при условии, что входящий поток заявок П_вх и поток обслуживаний П_об регулярные, то очереди вообще не будет, и каналы будут обслуживать заявки непрерывно. Но как только или входящий поток заявок П_вх или поток обслуживаний П_об перестаёт быть регулярным и приобретают элементы случайности, очередь начинает расти до бесконечности.

Итак, если l≥nm, т.е. СМО с ожиданием без ограничений на очередь перегружена, то есть нагрузка на один канал 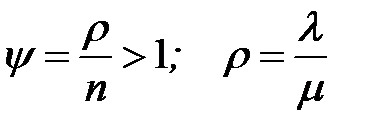, то предельный режим не устанавливается и предельных вероятностей состояний не существует.

Только, если l<nm, или нагрузка на один канал 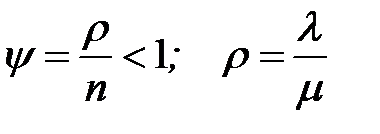, то предельный режим устанавливается и предельные вероятности состояний существуют.

Таблица 8.13 - Параметры многоканальной СМО с ожиданием

№ п/п	Параметры	Обозначения, значения, формулы
1.	Число каналов обслуживания	n≥1
2.	Максимальная длина очереди (максимальное число мест в очереди)	m®¥
3.	Интенсивность входящего простейшего потока заявок Пвх	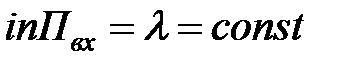, (l не зависит от времени t)
4.	Производительность каждого канала – интенсивность простейшего «потока обслуживаний» Поб (среднее число заявок, обслуживаемое одним каналом за единицу времени при непрерывной его работе без простоя)	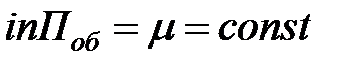, (m не зависит от времени t)
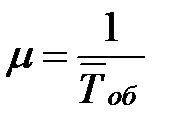5.	Соотношения между n, l и m	l<nm

Таблица 8.14 - Предельные характеристики эффективности функционирования многоканальной СМО с ожиданием

№ п/п	Предельные характеристики	Обозначения, формулы
1.	Приведённая интенсивность входящего потока - трафик (показатель нагрузки СМО)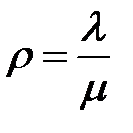
2.	Показатель (коэффициент) нагрузки, приходящейся на один канал - трафик (показатель нагрузки СМО)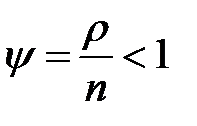
3.	Вероятность того, что все каналы свободны (вероятность простаивания всей системы)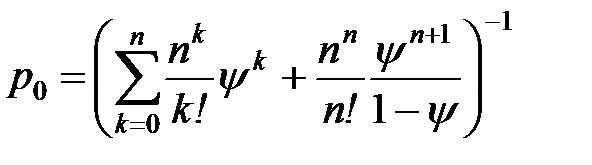
4.	Вероятности состояний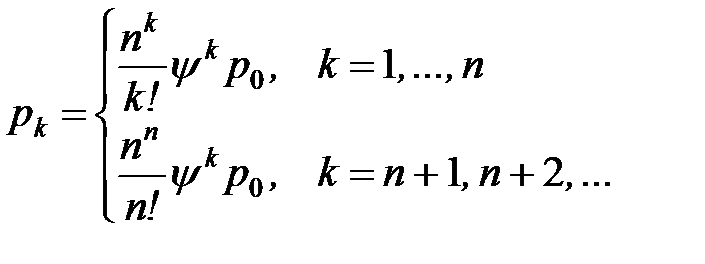
5.	Вероятность отказа заявке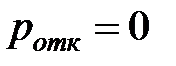
6.	Вероятность того, что заявка будет принята в СМО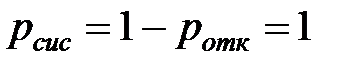
7.	Относительная пропускная способность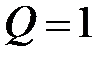
8.	Абсолютная пропускная способность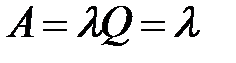

Продолжение таблицы 8.14

№ п/п	Предельные характеристики	Обозначения, формулы
9.	Среднее число занятых каналов – среднее число заявок, находящихся под обслуживанием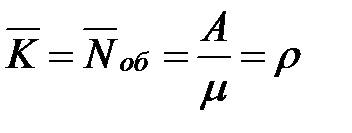
10.	Среднее число заявок, находящихся в очереди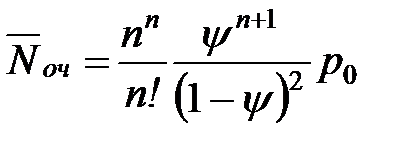
11.	Среднее число заявок находящихся в СМО (как в очереди, так и под обслуживанием)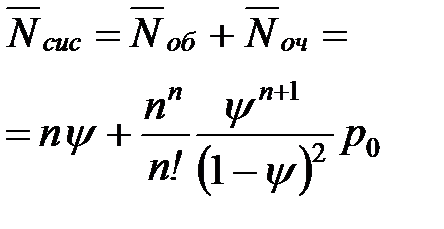
12.	Среднее время ожидания заявки в очереди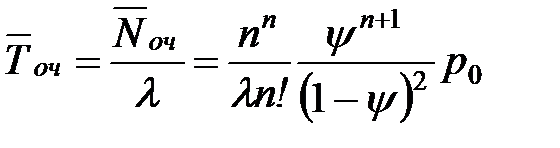
13.	Среднее время пребывания заявки в системе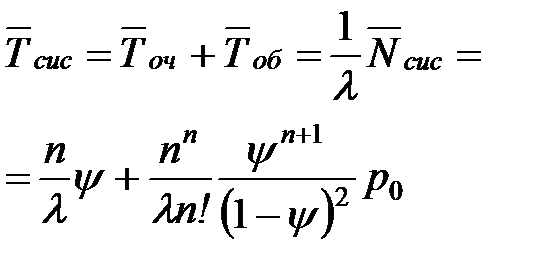
14.	Среднее время обслуживания одной заявки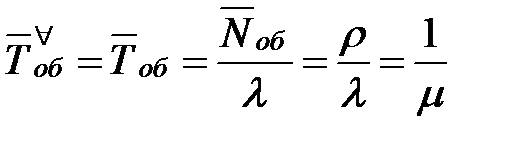

Задача 8.6

В кассе метрополитена, продающей жетоны на проезд, имеется два окна. Время, которое тратит кассир на обслуживание одного пассажира, в среднем равно 0,5 мин. Пассажиры подходят к кассе в среднем по 3 чел./мин).

Определить вероятности состояний СМО и основные характеристики эффективности функционирования данной кассы в предельном режиме:

· Среднее число занятых кассиров;

· Среднее число пассажиров в очереди;

· Среднее число пассажиров у касс;

· Среднее время, которое пассажир проводит в очереди;

· Среднее время, которое пассажир тратит на приобретение жетона.

Решение:

В условиях задачи математической моделью кассы метрополитена является многоканальная СМО с ожиданием без ограничений на длину очереди и на время ожидания, имеющая своими параметрами:

число каналов n=2;

интенсивность входящего потока 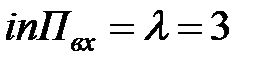(чел./мин);

среднее время обслуживания 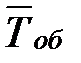=0,5 мин;

интенсивность потока обслуживаний 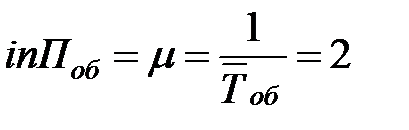(чел./мин);

показатель нагрузки СМО 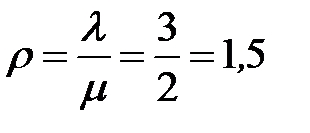(эрланга);

показатель нагрузки, приходящийся на один канал 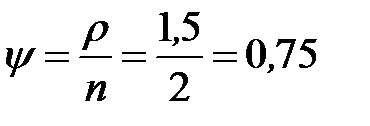(эрланга).

Так как l=3<nm=4, или нагрузка на один канал y=0,75<1, то предельный режим устанавливается и предельные вероятности состояний существуют.

Определим вероятность того, что все каналы свободны (вероятность простаивания всей системы):

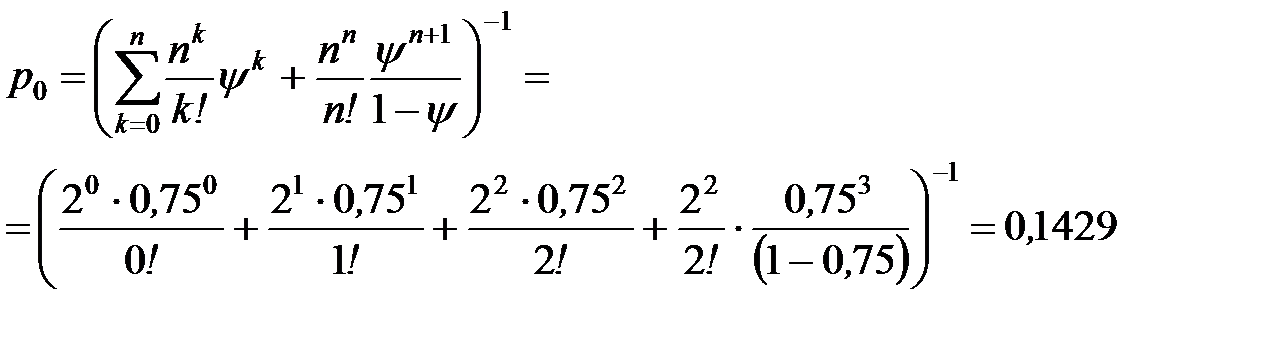
- то есть в вероятность того, что оба кассира свободны или того, что у кассы нет ни одного пассажира равна 0,1429.

Определим вероятность состояний СМО:

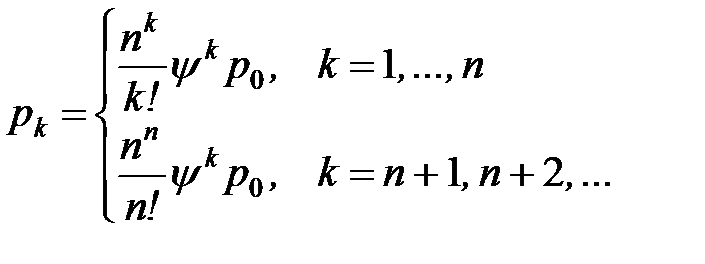
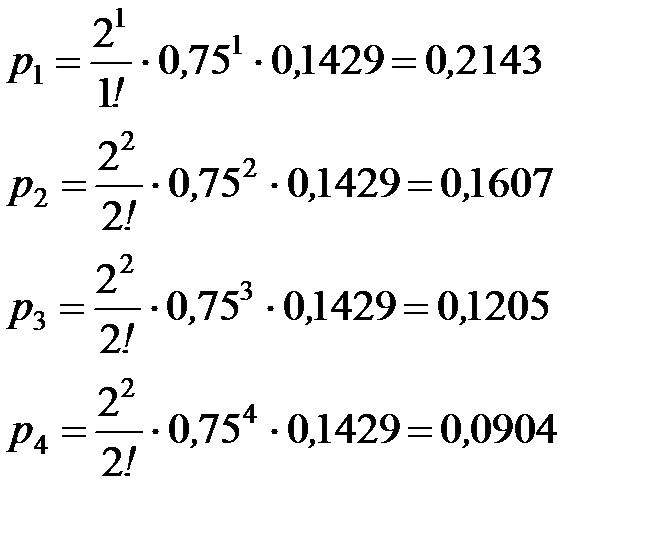
- то есть в вероятности того, что у касс:

1 пассажир равна 0,2143;

2 пассажира равна 0,1607;

3 пассажира равна 0,1205;

4 пассажира равна 0,0904 и т.д.

Аналогично можно рассчитать следующие вероятности (занесём их в таблицу 8.15):

Таблица 8.1

Вероятности состояний	Рассчитанные значения		Вероятности состояний	Рассчитанные значения
р0	0,1429		р11	0,0121
р1	0,2143		р12	0,0091
р2	0,1607		р13	0,0068
р3	0,1205		р14	0,0051
р4	0,0904		р15	0,0038
р5	0,0678		р16	0,0029
р6	0,0509		р17	0,0021
р7	0,0381		р18	0,9973
р8	0,0286		р19	0,0012
р9	0,0215		р20	0,0009
р10	0,0161		итого	0,9973®1

Определим число занятых каналов – среднее число заявок, находящихся под обслуживанием:

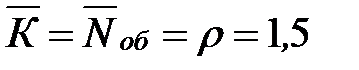- то есть в установившемся режиме среднее число занятых кассиров или среднее число пассажиров под обслуживанием составляет 2 человека.

Определим среднее число заявок в очереди:

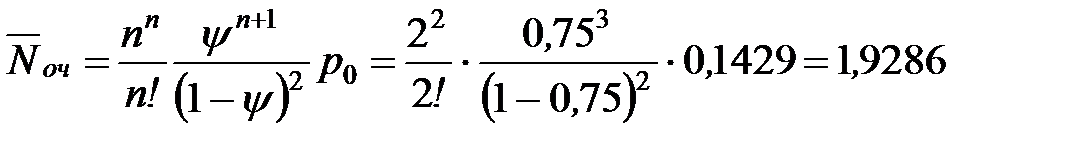
- то есть в установившемся режиме среднее число пассажиров в очереди равно двум.

Определим среднее число заявок, находящихся в системе:

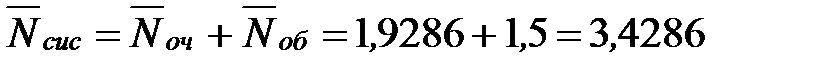- то есть в установившемся режиме среднее число пассажиров у касс равно трём.

Определим среднее время ожидания заявки в очереди:

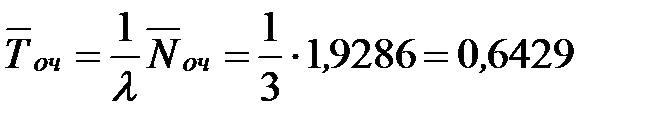- то есть в установившемся режиме среднее время ожидания пассажира в очереди составляет 0,6 минуты.

Определим среднее время пребывания заявки в СМО:

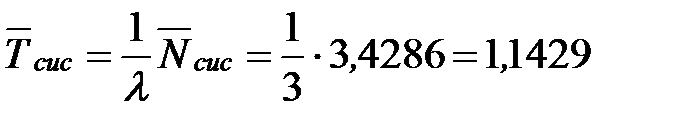- то есть в установившемся режиме среднее время, которое тратит пассажир на приобретение билета, составляет 1,1 минуты.

Итак, рассмотрены некоторые виды СМО. В рекомендуемой литературе следует ознакомиться самостоятельно и разобрать задачи по другим СМО.

Контрольные вопросы

1. Чему равно число состояний для n-канальной СМО с ожиданием?

2. Когда существуют предельные вероятности состояний для n-канальной СМО с ожиданием?

3. Чему равно среднее число заявок под обслуживанием n-канальной СМО с ожиданием?

4. Чему равно среднее число занятых каналов для n-канальной СМО с ожиданием?

5. При каких условиях вероятность отказа равна нулю для n-канальной СМО с ожиданием?

6. При каких условиях вероятность того, что пришедшая заявка будет принята в систему равна 1 для n-канальной СМО с ожиданием?

7. Чему равна абсолютная пропускная способность для n-канальной СМО с ожиданием?

Рекомендации по оформлению контрольной работы

Выбор варианта для решения задач выбирается исходя из последней цифры зачетной книжки. Решить необходимо 4 задачи. Задачи необходимо решить в рабочей тетради самостоятельно. Решение представить преподавателю во время семестра.

На практических и лабораторных занятиях решения задач автоматизируются с помощью пакета прикладных программ: MathCAD, MathLab, MS Excel.

Отчет представляется в виде файла проекта MathCAD, MathLab, MS Excel.

Задания для контрольной работы

Задача № 1

Одноканальная телефонная линия. Заявка-вызов, поступившая в момент, когда линия занята, получает отказ. Простейший поток заявок поступает с интенсивностью 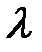звонков/ч. Время обслуживания заявки есть случайная величина, которая подчиняется экспоненциальному закону распределения. Средняя продолжительность разговора 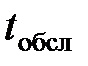мин. Изобразить структуру СМО и размеченный граф состояний, найти предельные вероятности состояний. Определить числовые характеристики и показатели эффективности работы системы.

вариант

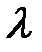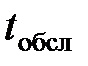Задача № 2

Многоканальная телефонная линия. Заявка-вызов, поступившая в момент, когда все n канала заняты, получает отказ. Простейший поток заявок поступает с интенсивностью 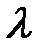звонков/ч. Время обслуживания заявки есть случайная величина, которая подчиняется экспоненциальному закону распределения. Средняя продолжительность разговора 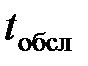мин. Изобразить структуру СМО и размеченный граф состояний, найти предельные вероятности состояний. Определить числовые характеристики и показатели эффективности работы системы.

вариант
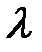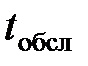n

Задача №3

Маленький магазин с одним продавцом. Предполагается, что простейший поток покупателей поступает с интенсивностью 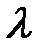человек/ч. Время обслуживания одного покупателя есть случайная величина, которая подчиняется экспоненциальному закону распределения с параметром 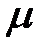человек/ч. При занятости продавца образуется очередь размером m. Изобразить размеченный граф состояний, найти предельные вероятности состояний. Определить числовые характеристики и показатели эффективности работы системы.

Как измениться эффективность работы системы, если в магазине будут работать 2 продавца.

вариант
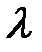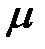m

Задача №4

На склад для разгрузки поступает простейший поток грузовиков с интенсивностью 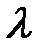грузовиков/ч. Время обслуживания одного грузовика есть случайная величина, которая подчиняется экспоненциальному закону распределения. Средняя продолжительность разгрузки одного грузовика 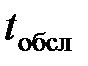мин. Количество терминалов для разгрузки n. Размер стоянки ограничен числом m. Изобразить структуру СМО и размеченный граф состояний, найти предельные вероятности состояний. Определить числовые характеристики и показатели эффективности работы системы.

вариант
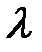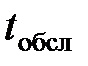n
m

Список литературы

Основная литература

1. Советов Б. Я. Моделирование систем : учеб. пособие / Б. Я. Советов, С. А. Яковлев. – М. : Высшая школа, 2009. – 344 с.

2. Вентцель Е.С, Овчаров Л.А. Теория вероятностей и ее инженерные приложения. / Е.С. Вентцель, Л.А. Овчаров. – М.: Высш.шк., 2008. – 480 с.

3. Тихоненко О. М. Модели массового обслуживания в информационных системах: Учебное пособие для вузов / О.М. Тихоненко – Минск: «Технопринт», 2003. – 326 с.

Дополнительная литература

1. Клейнрок Л. Теория массового обслуживания. Пер. с англ. – М.: Машиностроение, 1979. – 254 с.

2. Бусленко Н. П. Моделирование сложных систем : учеб. пособие / Н. П. Бусленко. – М. : Наука, 1968. – 356 с.

[1] Теоретически в общем случае система определяется как целостное множество взаимосвязанных элементов, которое нельзя расчленить на независимые подмножества.

[2] Потоком событий (в данном случае, заявок) называют последовательность событий, наступающих одно за другим в какие-то заранее неизвестные, случайные моменты времени.

[3] Случайным процессом (или случайной функцией) называется соответствие, при котором каждому значению аргумента (в данном случае — моменту из промежутка времени проводимого опыта) ставится в соответствие случайная величина (в данном случае — состояние СМО).

[4] Случайный процесс, протекающий в СМО, называется марковским (или процессом без последействия, или процессом без памяти), если вероятность любого состояния СМО в будущем зависит только от ее состояния в настоящем и не зависит от.ее состояний в прошлом.

[5] Поток событий, обладающий свойствами отсутствия последействия (для любых двух непересекающихся промежутков времени число событий, наступающих за один из них, не зависит от числа событий, наступающих за другой) и ординарностью (вероятность наступления за элементарный — малый промежуток времени более одного событий пренебрежимо мала по сравнению с вероятностью наступления за этот промежуток времени одного события), называется пуасооновским.

[6] Вообще, для многоканальной СМО n≥2, под условием n≥1 будем понимать, что при случае n=1 одноканальная СМО может быть рассмотрена, как частный случай многоканальной СМО и вычисления по ниже приведённым формулам не приведут к ошибкам, но лучше работать с приведёнными выше формулами для одноканальная СМО, что проще.

[7] Вообще, для многоканальной СМО n≥2, под условием n≥1 будем понимать, что при случае n=1 одноканальная СМО может быть рассмотрена, как частный случай многоканальной СМО и вычисления по ниже приведённым формулам не приведут к ошибкам, но лучше работать с приведёнными выше формулами для одноканальная СМО.