Формулировка математической модели задачи
ü переменные для решения задачи: X1 - суточный объем производства материала А, Х2 - суточный объем производства материала В;
ü определение функции цели (критерия оптимизации). Суммарная суточная прибыль от производства X1, материала А и Х2 материала В равна:
F = 4000Х2 +3000Х1,
поэтому цель фабрики - среди всех допустимых значений X1 и Х2 найти такие, которые максимизируют суммарную прибыль от производства материалов F:
F = 4000Х2 + 3000 Х1, -> max;
ü ограничения на переменные:
§ объем производства красок не может быть отрицательным, т. е.
Х2 >=0,Х1 >=0;
§ расход исходного продукта для производства обоих видов материалов не может превосходить максимально возможного запаса данного исходного продукта, т.е.:
2Х2 + 3Х1 <= 7, 3Х2 + 2Х1 <= 9.
§ ограничения на величину спроса на материалы:
Х1 - Х2 <= 1, Х1 <= 3.
Таким образом, получена следующая математическая модель задачи:
ü необходимо найти максимум следующей функции:
F = 4000Х2 + 3000Х1 -> max
ü при ограничениях вида:
2Х2 +3Х1, <= 7, 3Х2 + 2Х1, <= 9,
Х1 - Х2 <= 1, Х1 <= 3, Х1, >= 0, Х2 >= 0.
Решение задачи с помощью надстройки Поиск решения
ü подготовку рабочего листа MS Excel для задачи необходимо осуществить в соответствии с рисунком 2.1 (нужно ввести текст, данные и формулы).

Рисунок 2.1 Рабочий лист MS Excel для решения задачи
Планирование производства материалов
Переменные задачи Х1 и Х2 находятся, соответственно, в ячейках СЗ и С4. Целевая функция находится в ячейке С6 и содержит формулу: =4000*С4+3000*С3. Ограничения на задачу учтены в ячейках C8:D11.
ü ввод данных в окно Поиск решения необходимо произвести в соответствии с рисунком 2.2.
Воспользовавшись командой Сервис - Поиск решения,нужно ввести необходимые данные для рассматриваемой задачи (установка данных в окне Поиск решенияприведена на рисунке 2.2).
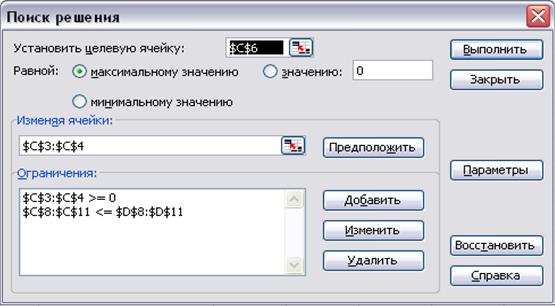
Рисунок 2.2 Установка необходимых параметров задачи планирования материалов в окне Поиск решения
ü полученное оптимальное решение представлено на рисунке 2.3.
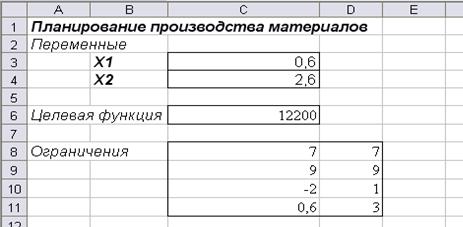
Рисунок 2.3Результат расчета с помощьюнадстройки Поиск решения
Вопросы для самоконтроля знаний
4.1 Что такое линейное программирование?
4.2 Что такое задача нелинейного программирования?
4.3 Какую опцию нужно установить в окне Параметры поиска решения для решения задач по линейному программированию?
4.4 Назовите виды задач линейного программирования.
Лабораторная работа №3
«Решение транспортных задач методом оптимизации с помощью надстройки Поиск решения»
Цель работы:Овладеть приемами работы с надстройкой Поиск решения при решении транспортных задач. Научиться:
ü находить оптимальное решение задачи с помощью надстройки Поиск решения при решении транспортных задач;
ü создавать отчеты по результатам поиска решения;
ü сохранять параметры модели.
Общие сведения
Транспортная задача
В общем виде транспортную задачу можно сформулировать следующим образом: в m пунктах отправления А1,...,Аm находится однородный груз, количество которого равно соответственно а1,...,аm единиц. Данный груз необходимо доставить потребителям B1,...,Вn, спрос которых - b1,...,bn. Стоимость перевозки единицы груза из i-го (i = 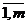 ) пункта отправления в j-й (j =
) пункта отправления в j-й (j = 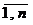 ) пункт назначения равна Сi,j. Необходимо составить план перевозок, который полностью удовлетворяет спрос потребителей в грузе, и при этом суммарные транспортные издержки минимальны.
) пункт назначения равна Сi,j. Необходимо составить план перевозок, который полностью удовлетворяет спрос потребителей в грузе, и при этом суммарные транспортные издержки минимальны.
Математически транспортную задачу можно записать так:
F = 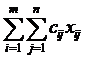
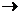 min, (1)
min, (1)
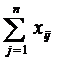 = ai,, i =
= ai,, i = 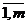 ,
, 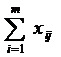 = bj,, j =
= bj,, j = 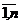 , (2)
, (2)
xij >= 0, i = 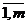 , j =
, j = 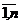 . (3)
. (3)
Таким образом, дана система ограничений (2) при условии (3) и линейная функция (1). Требуется среди множества решений системы (2) найти такое неотрицательное решение, которое доставляет минимум линейной функции (1).
Модель транспортной задачи называют закрытой (сбалансированной), если суммарный объем груза, имеющегося у поставщиков, равен суммарному спросу потребителей, т. в. выполняется равенство:
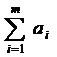 =
= 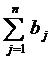 .
.
Если для транспортной задачи выполняется одно из условий:
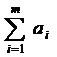 >
> 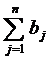 ,
, 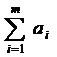 <
< 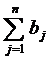 ,
,
то модель задачи называют открытой (несбалансированной).
Для разрешимости транспортную задачу с открытой моделью следует преобразовать в закрытую.
ü Так, если выполняется условие 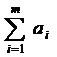 >
> 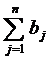 , то необходимо ввести фиктивный (n+1)-й пункт назначения Вn+1, т. е. в матрицу задачи вводится дополнительный столбец. Спрос фиктивного потребителя принимается равным bn+1 =
, то необходимо ввести фиктивный (n+1)-й пункт назначения Вn+1, т. е. в матрицу задачи вводится дополнительный столбец. Спрос фиктивного потребителя принимается равным bn+1 = 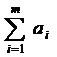 -
- 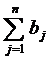 . Стоимость перевозок продукции полагается одинаковой, чаще всего равной нулю (если не задана стоимость складирования продукции), т. е. сi,n+1 = 0, i =
. Стоимость перевозок продукции полагается одинаковой, чаще всего равной нулю (если не задана стоимость складирования продукции), т. е. сi,n+1 = 0, i = 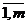 .
.
ü Если выполняется условие 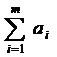 <
< 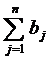 , то необходимо ввести фиктивного (m+1)-го поставщика Am+1, т. е. в матрицу задачи вводится дополнительная строка. Запас груза данного поставщика принимается равным am+1 =
, то необходимо ввести фиктивного (m+1)-го поставщика Am+1, т. е. в матрицу задачи вводится дополнительная строка. Запас груза данного поставщика принимается равным am+1 = 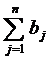 -
- 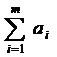 . Стоимость перевозок продукции полагается одинаковой, чаще всего равной нулю (если не задана стоимость штрафов за недопоставку продукции), т. е. cm+1,j = 0, j =
. Стоимость перевозок продукции полагается одинаковой, чаще всего равной нулю (если не задана стоимость штрафов за недопоставку продукции), т. е. cm+1,j = 0, j = 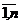 . При преобразовании открытой задачи в закрытую целевая функция не меняется, т. к. все слагаемые, соответствующие дополнительным перевозкам, равны нулю.
. При преобразовании открытой задачи в закрытую целевая функция не меняется, т. к. все слагаемые, соответствующие дополнительным перевозкам, равны нулю.
Содержание работы
2.1 Запустить программу MS Excel.
2.2 Создать файл аналогичный примеру 1 (Транспортные расходы).
2.3 Рассмотреть все варианты нахождения оптимального решения в примере 1, установив надстройку Поиск решения.
2.4 Найти оптимальное решение с помощью надстройки Поиск решения) в заданиях для самостоятельного решения из Приложения В. Вариант задания выбирается по указанию преподавателя.
2.5 Создать один из видов отчетов по результатам поиска решения.
2.6 Ответить на контрольные вопросы.
2.7 Составить отчет о проделанной работе, который должен содержать название работы, постановку задачи исследования, сведения о последовательности выполнения заданий с результатами и ответы на контрольные вопросы, указанные преподавателем.
3 Методика выполнения работы. Нахождение оптимального решения транспортной задачи с помощью надстройки Поиск решения на примере задачи Транспортные расходы
Работу с надстройкой Поиск решения рассмотрим на примере транспортной задачи.
Пример 1. Транспортные расходы
Производство продукции осуществляется на 4-х предприятиях, затем развозится в 5 пунктов потребления. Предприятия могут выпускать в день 235, 175, 185 и 175 единиц продукции. Пункты потребления готовы принимать ежедневно 125, 160, 60, 250 и 173 единиц продукции. Хранение на предприятии единицы продукции обходится в 2 у.е. в день, штраф за недопоставленную продукцию 3,5 у.е. в день. Стоимость перевозки единицы продукции (в у.е.) с предприятий в пункты потребления приведены в таблице 3.1.
Необходимо минимизировать суммарные транспортные расходы по перевозке продукции.
Таблица 3.1 Транспортные расходы
| Предприятия | Пункты потребления | ||||
| 3,2 | 2,35 | 3,65 | |||
| 2,85 | 2,5 | 3,9 | 3,55 | ||
| 3,75 | 2,5 | 2,4 | 3,5 | 3,4 | |
| 2,1 | 4,1 | 3,4 |
