I. Повторение и обобщение изученного материала.
Сценка. Заходят три девочки: на груди первой плакат с дробью 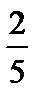 , у второй –
, у второй – 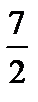 , а у третьей
, а у третьей 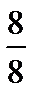 (девочек предварительно подготовить). «Здравствуйте, мы Обыкновенные Дроби. А сейчас мы проверим, что вы о нас знаете». Вперед выходит «Дробь
(девочек предварительно подготовить). «Здравствуйте, мы Обыкновенные Дроби. А сейчас мы проверим, что вы о нас знаете». Вперед выходит «Дробь 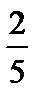 » и задает вопросы.
» и задает вопросы.
1) Как называется число 2? Где записывается числитель?
2) Как называется число 5? Где записывается знаменатель?
3) Что показывает знаменатель? Что показывает числитель?
4) Что вы еще можете обо мне сказать? ( 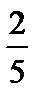 – правильная дробь (объяснить), её можно изображать на числовом луче (как?); дробь можно записать в виде частного (дробь
– правильная дробь (объяснить), её можно изображать на числовом луче (как?); дробь можно записать в виде частного (дробь 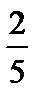 меньше 1).
меньше 1).
Выходит вперед «Дробь 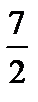 » (также предлагает вопросы классу: что еще можно сказать о дроби
» (также предлагает вопросы классу: что еще можно сказать о дроби 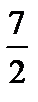 ?…), а потом задает вопрос: чем отличается дробь
?…), а потом задает вопрос: чем отличается дробь 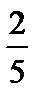 от дроби
от дроби 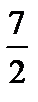 ? (
? ( 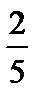 – правильная дробь, а
– правильная дробь, а 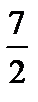 – неправильная). Выходит «Дробь
– неправильная). Выходит «Дробь 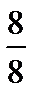 », и ученики делают вывод, что дробь
», и ученики делают вывод, что дробь 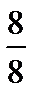 тоже неправильная, и продолжается беседа о неправильных дробях.
тоже неправильная, и продолжается беседа о неправильных дробях.
II.Какие математические операции можно выполнить с обыкновенными дробями? (Сравнивать, складывать, вычитать) – повторить правила. Ученики оценивают.
Примечание: так как это урок самооценки знаний, то на каждый ряд раздать листки по форме:
| № п/п | Фамилия, имя учащегося | Теоретическая часть | Выделение целой части числа | Записать в виде неправильной дроби | Сложение и вычитание дробей | Итоговая оценка |
| Иванов С. | ||||||
| Петров Е. | ||||||
| Сидоров А. |
III. Тренировочные упражнения.
1. Выделить целую часть:
а) из дробей: 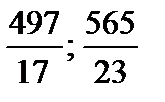 .
.
б) из дробной части: 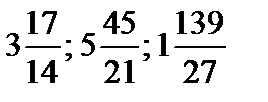 .
.
2. Записать в виде неправильной дроби смешанные числа: 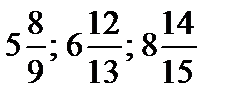 .
.
3. Записать числа в порядке убывания: 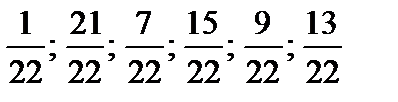 .
.
4. Выполнить действия:
а) 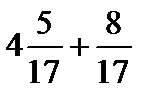 ; г)
; г) 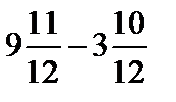 ;
;
б) 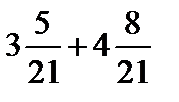 ; д)
; д) 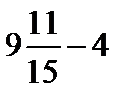 ;
;
в) 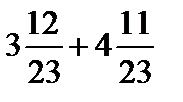 ; е)
; е) 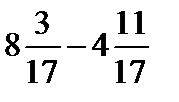 .
.
IV. Домашнее задание: № 1820, 1821, 1822, 1823. Повторить действия с десятичными дробями.
Урок № 161
Сложение, вычитание, умножение
И деление десятичных дробей
Оборудование: индивидуальные карточки.
Ход урока
I. Устные упражнения.
1. Правила выполнения действий с десятичными дробями повторяются, уточняются во время устных упражнений.
Вычислить:
| а) 3 + 0,3 0,01 + 0,03 0,007 + 0,02 0,02 + 0,004 | б) 3,75 – 2 6,5 – 0,4 15,8 – 3,4 3,25 – 2,1 | в) 6 × 0,6 7 × 0,02 0,5 × 0,08 4,2 × 1,5 + 4,2 × 0,5 2 × 3,9 × 0,5 4 × 7,8 × 0,25 | г) 24,6 : 3 6,8 : 2 0,08 : 2 2 : 0,2 2,4 : 1,2 0,8 : 0,02 |
2. Округлить число 37,2573 до тысячных, сотых, десятых, единиц.
3. Игра «Заполни клетку».
Учащиеся получают листочки, текст которых приведен в таблице.
| Вариант I. Фамилия________ | Вариант II. Фамилия________ | |
1,4 + 0,6 =   – 1,7 = – 1,7 =   × 1,2 = × 1,2 =   : 9 = : 9 =   + 0,96 = + 0,96 =   – 0,2 = – 0,2 =   × 0,5 = × 0,5 =   : 0,02 = : 0,02 =  | 2,6 + 0,04 =   – 2,8 = – 2,8 =   × 1,8 = × 1,8 =   : 12 = : 12 =   + 0,97 = + 0,97 =   – 0,1 = – 0,1 =   × 0,5 = × 0,5 =   : 0,15 = : 0,15 =  |
Примечание: Правило заполнения клеток состоит в том, что ответ предыдущего действия ставится в первую клетку следующего.
II. Выполнение письменных упражнений.
1. № 1834 (д, е).
2. Самостоятельно № 1836 (а).
3. № 1835 (а), 1836 (а).
III. Итог урока.
Соревнование «Думай и соображай».
1. Какой знак можно поставить между числами 7 и 8, чтобы получившееся число было больше 7 и меньше 8?
2. Между числами 7,3 и 7,4 поставьте число, большее 7,3 и меньшее 7,4.
3. Даны числа: 0,3; 7,7; 0,125. Поставьте между ними такие знаки, чтобы в результате выполнения указанных вами действий получилась единица. (Ответ: (0,3 + 7,7) × 0,125).
4. Найти устно значение выражения: (13 – 2,46 : 3,54) × (0,5 – 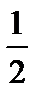 ).
).
IV. Домашнее задание:№ 1834 (а, б), 1835 (б), 1836 (б).
Урок № 162
Решение уравнений
Оборудование: ксерокопии текстов каждого варианта.
Ход урока
I. Проверка домашнего задания.
Выполнить тест.
Вариант I
1. Вычислите: 3,34 + 28,7.
1) 32,04; 2) 31,41; 3) 31,04; 4) 62,1.
2. Вычислите: 0,34 × 0,8.
1) 2,72; 2) 0,272; 3) 27,2; 4) 0,0272.
3. Вычислите: 20,4 : 0,8.
1) 25,5; 2) 2,55; 3) 0,255; 4) 255
4. Округлите 0,6539 до сотых.
1) 0,7; 2) 0,65; 3) 0,66; 4) 0,654.
5. Расположите в порядке убывания числа 3,78; 3,784; 3,7801.
1) 3,7801; 3,78; 3,784; 2) 3,784; 3,78; 3,7801;
3) 3,784; 3,7801; 3,78; 4) 3,78; 3,7801; 3,784.
6. Выразите в метрах 0,002 км.
1) 20 м; 2) 200 м; 3) 2 м; 4) 2000 м.
7. Найдите площадь квадрата, сторона которого равна 1,1 дм.
1) 4,4 дм2; 2) 1,21 дм2; 3) 2,2 дм2; 4) 121 дм2.
8. Из чисел 1; 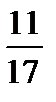 ; 1,05;
; 1,05; 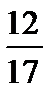 выберите наименьшее.
выберите наименьшее.
1) 1; 2) 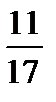 ; 3) 1,05; 4)
; 3) 1,05; 4) 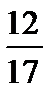 .
.
| Фамилия, имя____________________________ класс________ | ||||||||
| № задания | ||||||||
| № ответа |
Вариант II
1. Вычислите: 6,35 – 3,5.
1) 2,85; 2) 3,3; 3) 6; 4) 3,85.
2. Вычислите: 0,7 × 0,26.
1) 0,182; 2) 0,0182; 3) 1,82; 4) 18,2.
3. Представьте в виде десятичной дроби 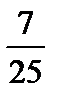 .
.
1) 0,725; 2) 0,28; 3) 0,028; 4) 2,8
4. Округлите 0,2518 до десятых.
1) 0,25; 2) 0,2; 3) 0,3; 4) 0,251.
5. Расположите в порядке возрастания числа 1,4302; 1,43; 1,437.
1) 1,437; 1,4302; 1,43; 2) 1,43; 1,4302; 1,437;
3) 1,437; 1,43; 1,4302; 4) 1,4302; 1,43; 1,437.
6. Выразите в тоннах 16 кг.
1) 0,16 т; 2) 0,00016 т; 3) 0,0016 т; 4) 0,016 т.
7. Найдите периметр квадрата, сторона которого равна 1,3 дм.
1) 16,9 дм; 2) 2,6 дм; 3) 5,2 дм; 4) 1,3 дм.
8. Из чисел 0,98; 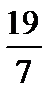 ; 1;
; 1; 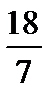 выберите наибольшее.
выберите наибольшее.
1) 0,98; 2) 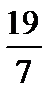 ; 3) 1; 4)
; 3) 1; 4) 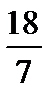 .
.
| Фамилия, имя____________________________ класс________ | ||||||||
| № задания | ||||||||
| № ответа |
II. Устные упражнения.
1. Решите уравнения. Заполните таблицу буквами, учитывая найденные ответы.
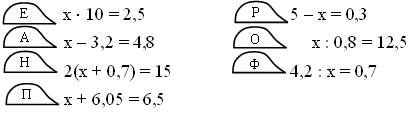
| 0,45 | 4,7 | 0,25 | 6,8 | 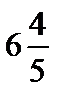 | |||
Что означает полученное слово?
(Ответ: Парфенон, храм Афины Парфенос на Акрополе в Афинах, памятник древнегреческой высокой классики, построен в 432 г. до н. э.)
2. Найдите корни уравнения:
х × 1 = 0 0 × х = 1 х – х = 0 х – х = 1
х – 10 = 10 х + 10 = 10 0 × х = 0 0 + х = 10
х – 10 = 0 х : 10 = 10 0 : х = 1.
III. Тренировочные упражнения:
1. Решить уравнение:
а) (х – 5,6) : 12 = 3,7 б) (х + 2,1) × 4 = 15,2 (2-я способами)
в) 3,4 – 9х = 1,6 г) 8,1 : х – 0,7 = 3
д) s : 2,3 = 4,6 е) 9,88 : (6,7 – х) = 2,6
ж) 6,7 × (7,9 – у) = 28,81 з) 9,14z – (3,78z + 2,87z) = 12,45.
2. Решить самостоятельно:
а) 41 – 7,08у = 23,3 б) 4,6х + 3,8х –1,6 = 0,5
IV. Итог урока.
1. Можно привести высказывание Д. Чосера:
«Посредством уравнений, теорем
Он уйму всяких разрешил проблем:
И засуху предсказывал, и ливни.
Поистине его познанья дивны».
2. Решить уравнения:
а) 0,3х + 2,4 х = 270; б) 0,2 × (4х + х) = 12; в) 2х + х + 0,6 = 4,2.

Используя найденные ответы, узнайте имена клоунов, если известно, что у Бима корень уравнения совпадает с ответом примера 40 × 1,25 × 0,8 × 2,5 =…, а у Бома корень уравнения наименьший. Третьего клоуна зовут Бум.
V. Домашнее задание: № 1817, 1828, 1876.
Урок № 163
Решение задач
Оборудование: плакат «Недостаточно лишь понять задачу, необходимо желание решить её. Без сильного желания решить трудную задачу невозможно, но при наличии такового возможно. Где есть желание, найдется путь!» (Д. Пойа).
Ход урока
I. Проверка домашнего задания.
1. Консультанты докладывают об итогах выполнения домашнего задания.
2. Соседи по парте обмениваются тетрадями, проверяют, исправляют и оценивают.
II. Устные упражнения.
1. Блиц-турнир.
1) В одной бригаде – х человек, а в другой – в 2 раза больше. Сколько человек в двух бригадах вместе?
2) Ботинки стоят х рублей, и они на 20 рублей дешевле шляпы.
а) Сколько стоит шляпа?
б) Сколько стоят ботинки и шляпа вместе?
3) Футбольный мяч стоит у рублей. Его цена была снижена на 25%. Какова новая цена мяча?
4) Чайный сервиз стоил 600 рублей. Через некоторое время цена его была снижена на х%. Сколько теперь стоит сервиз?
5) Свитер стоил у рублей. Его цена увеличилась наполовину. Сколько стал стоить свитер?
6) Рабочий делает х деталей за минуту. Сколько деталей он сделает за 1 час?
2. Переведите на математический язык каждое предложение и запишите его в виде равенства, если х – это количество яблок; у – количество груш.
1) Яблок в корзине столько же, сколько груш:_____________
2) Яблок на 6 меньше, чем груш: ________________________
3) Яблок в 3 раза больше, чем груш: _____________________
