Кубическая оценка времени работы

Оценим время работы нашего алгоритма.

Всего n фаз. В фазе i продлеваем i суффиксов. Причем, j-й суффикс в этой фазе tj . . . ti имеет длину

i − j + 1. Тогда продление j в фазе i требует время O(i − j). Поэтому сначала суммируем по j, чтобы

узнать стоимость фазы i. Далее суммируем по i, получая оценку времени работы всего алгоритма. Итого:

O(Pn(i=1)Pi(j=1)i − j) = O(n^3).

Квадратичный алгоритм

Идея вспомогательных данных

Вначале объясним стандартную идею из теории алгоритмов. Допустим, нужно вычислить массив

X1, . . . ,Xn по индукции. В таком случае для вычисления очередного элемента Xi+1 может не хватить знания элемента Xi, то есть могут потребоваться дополнительные данные. Поэтому иногда полезно определить вспомогательный массив Y1, . . . , Yn. Далее последовательно вычислять оба массива, то есть сначала

вычислить X1 и Y1, с их помощью вычислить X2, затем вычислить Y2, и так далее. И, наконец, с помощью Xn−1 и Yn−1 вычислить Xn.

Далее нам также потребуются вспомогательные данные, в качестве которых выступят суффиксные

стрелки.

Определение суффиксных стрелок

Для каждой внутренней вершины, соответствующей суффиксу t1 . . . tk, нарисуем суффиксную стрелку

в вершину, соответствующую суффиксу t2 . . . tk. Заметим, что этот суффикс будет заканчиваться именно

в вершине, а не на ребре. Дело в том, что суффикс t1 . . . tk заканчивается во внутренней вершине, значит

он как подстрока уже встречался в исходном тексте как минимум с двумя различными продолжениями.

Поэтому, если отбросить первую букву t1, то строка t2 . . . tk тоже встречалась как минимум с двумя

различными продолжениями. Таким образом, суффикс t2 . . . tk тоже будет заканчиваться во внутренней вершине.

Рассмотрим пример на рисунке 10. Возьмем вершину v, в которую приходим по строке xa. Чтобы

провести суффиксную стрелку, отбросим первую букву x, осталась буква a. Прочитав ее от корня дерева, приходим в вершину u, это и есть адрес суффиксной стрелки. Теперь есть строка a, отбросим первую букву и получим пустую строку, которая соответствует корню дерева. Поэтому проводим вторую суффиксную стрелку в корень ST.

Обновление суффиксных стрелок с опозданием

Для начала отметим, что старые суффиксные стрелки сохраняются при продлениях суффиксов. По-

этому осталось понять, когда нужно рисовать новую суффиксную стрелку.

Рассмотрим случай на рисунке 11, когда мы применили продление по второму правилу (ответвление) к суффиксу tj . . . ti и в дереве образовалась новая внутренняя вершина v. Тогда вторым ребенком вершины v стал новый лист, на ребре к которому написана буква ti+1. Тогда из v нужно провести суффиксную стрелку.

Не будем отдельно искать место, куда должна указывать суффиксная стрелка. Просто перейдем к

продлению следующего суффикса. Это будет суффикс tj+1 . . . ti. Его конец и есть адрес суффиксной

стрелки. Возможно, что этот суффикс так же, как и предыдущий, заканчивается на ребре. Но тогда

7снова будет продление по второму правилу, и образуется нужная нам внутренняя вершина u, в которуюи проведем суффиксную стрелку из v.

Фаза с прыжками

Будем называть «хвостом» суффикса то место в суффиксном дереве, где мы остановимся, если будем

читать суффикс от корня дерева. Таким образом, «хвост» может быть как в вершине дерева, так и на

ребре. Тогда можно сэкономить на нахождении всех «хвостов» внутри одной фазы. Пусть мы закончили работу с «хвостом» j-го суффикса tj . . . ti, то есть выполнили один из трех типов продлений. Найдем теперь хвост (j + 1)-го суффикса с помощью техники «Вверх-Прыжок-Вниз».

Перейдем от j-го «хвоста» суффикса tj . . . ti вверх до ближайшей внутренней вершины, соответствующей строке tj . . . tk. Из нее будет существовать суффиксная стрелка, так как для каждой новой внутренней вершины создается суффиксная стрелка в той же фазе. Прыгнем по этой стрелке в вершину, соответствующую строке tj+1 . . . tk. Затем спустимся вниз по дереву, читая текст tk+1 . . . ti. Таким образом, приходим к хвосту суффикса tj+1 . . . ti.

Прыжки: подсчет высоты

Будем называть глубиной вершины в дереве число ребер, по которым надо пройти из корня, чтобы

попасть в вершину. Будем следить за глубиной указателя в дереве.

Сначала проходим по одному ребру вверх, уменьшая глубину вершины на 1. Далее переходим по

суффиксной стрелке, глубина уменьшается не более чем на 1. Это объясняется тем, что на пути Aв

дереве по суффиксу tj+1 . . . tk не более чем на одну вершину меньше, чем на пути B по суффиксу tj . . . tk, потому что в пути B каждой вершине v будет соответствовать одна вершина u пути A, в которую будет направлена суффиксная стрелка из v. Причем разница в одну вершину в этих путях может возникнуть, если в пути B первому ребру будет соответствовать единственная буква tj , тогда суффиксная стрелка из второй вершины после корня будет вести в корень.

Итак, после перехода вверх и прыжка по суффиксной стрелке глубина уменьшится не более чем на

2. Поэтому за фазу i вверх мы совершили не более 2i переходов. Но заметим, что внутри одной фазы

начальная глубина больше конечной, так как длины суффиксов в течение фазы уменьшаются до 1. Поэтому вниз мы не могли ходить больше, чем вверх. Таким образом, вниз мы тоже совершили не более 2iпереходов. Поэтому общая оценка навигации внутри фазы составляет 4i переходов.

Поскольку всего n фаз, в каждой из которых O(n) переходов, общее время работы алгоритма стало

O(n^2).

Линейный алгоритм

Анализ операций продления

Итак, есть три типа продлений:

1. Удлинение: продление листа.

2. Ответвление буквы.

3. Пустое правило.

Наблюдение 1: как только мы применили пустое правило, дальше в фазе все продления — пустые.

Допустим, у нас есть «хвост» суффикса α = tj . . . ti

, и дальше в дереве уже есть переход по следующей

букве z = ti+1, но он мог появиться только при продлении идентичного текущему суффикса такой же

буквой z.

В этом случае текст T = t1 . . . tn представляется, как на рисунке 13. Значит, все последующие продле-

ния тоже уже выполнялись, поскольку любой суффикс строки α продлялся ранее буквой z. Поэтому все оставшиеся продления в этой фазе будут пустыми.

«Живые» ребра

Наблюдение 2: после того, как мы применили правило ответвления и создали новый лист, в следующих фазах к этому листу всегда будет применяться правило удлинения.

В связи с этим можно улучшить наш алгоритм. При создании нового листа будем кодировать новое

ребро, ведущее в лист, как T[i+ 1, x], где x — указатель на переменную, хранящую конец текущего текста. Тогда все продления уже созданных листов можно произвести одной операцией x := x + 1. Заметим, что на этом ребре в дальнейшем могут происходить ответвления, тогда будет меняться начальный индекс i + 1, но не конечный.

Модификация алгоритма

Пусть «непустая часть» фазы i−1 закончилась на суффиксе j∗. Следовательно, к суффиксам 1, . . . , j∗

применялись только правила 1 и 2, и каждый из них заканчивается в своем собственном листе. Опишем алгоритм для фазы i.

1. Присваиваем x := x + 1, одновременно продляя все суффиксы 1..j∗.

2. Последовательно продляем суффиксы j∗ + 1, . . . , j0, где j 0 — первое применение пустого правила.

3. Обновляем номер суффикса, к которому последним применялось непустое правило j∗:= j0 − 1 и

переходим к следующей фазе.

Линейная оценка

Работу алгоритма можно представить в виде схемы, показанной на рисунке 14.

По горизонтали у нас расположены суффиксы по увеличению номеров, а значит по порядку рассмот-

рения в алгоритме. Жирные зеленые линии обозначают участки индивидуальных продлений в каждой

фазе, то есть это те суффиксы, которые продляются с ответвлением. Для всех суффиксов слева от зеленой

линии происходит продление листа путем увеличения переменной x := x+1. Черные точки соответствуют

моментам первого применения пустого правила в каждой фазе. Заметим, что на последней фазе не будет

пустых продлений, потому что продляем невстречавшимся ранее специальным символом $.

Оценим время работы алгоритма. Участки индивидуальных продлений по фазам перекрываются не

более чем по одному суффиксу (суффикс, на котором первый раз применяется пустое правило, в сле-

дующей фазе снова обрабатывается индивидуально). Суммарное количество прыжков при продлениях

линейно, как мы выяснили при анализе квадратичного алгоритма. Последняя фаза строит уже явное

суффиксное дерево текста. Вот мы и получили оценку O(n).

Итоги

Суффиксное дерево — способ представления текста.

Применения: поиск подстрок, поиск наибольшей общей подстроки.

Основные идеи алгоритма: on-line построение, использование вспомогательных суффиксных стрелок,

неравномерная оценка времени работы.

Суффиксный массив.

Cуффиксным массивом строки называется массив целых чисел от до 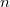, такой, что суффикс — -й в лексикографическом порядке среди всех непустых суффиксов строки .

Пример:

. Суффиксы в лексикографическом порядке:
1)
2)
3)
4)
5)
6)
7)
Значит, суффиксный массив для строки равен .

Применения:

Позволяет найти все вхождения образца 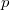в строку за время

Позволяет вычислить (longest common prefix) для всех соседних в лексикографическом порядке суффиксов строки за , то есть построить массив , где — длина наибольшего общего префикса суффиксов и .

Наивный алгоритм поиска

Простейший способ узнать, встречается ли образец в тексте, используя суффиксный массив, — взять первый символ образца и бинарным поиском по суффиксному массиву найти диапазон с суффиксами, начинающимися на такую же букву. Так как все элементы в полученном диапазоне отсортированы, а первые символы одинаковые, то оставшиеся после отбрасывания первого символа суффиксы тоже отсортированы. А значит, можно повторять процедуру сужения диапазона поиска уже по второму, затем третьему и так далее символу образца до получения либо пустого диапазона, либо успешного нахождения всех символов образца.

Бинарный поиск работает за время равное , а сравнение суффикса с образцом не может превышать длины образца.

Таким образом время работы алгоритмы , где — текст, 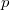— образец.