ТЕМА 2. Элементы векторной алгебры

Лекция № 3.

Тема:Векторы. Скалярное, векторное и смешанное произведение векторов

План:

1. Понятие вектора. Коллинарность, компланарность векторов.

2. Линейные операции над векторами.

3. Скалярное произведение векторов

4. Векторное произведение векторов

5. Смешанное произведение векторов

1. Понятие вектора.Коллинарность, компланарность векторов.

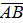Определение: Вектором называется направленный отрезок с начальной точкой А и конечной точкой В.

Обозначение: , ,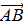

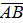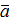
Определение: Длиной или модулем вектора 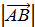вектора 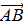называется число, равное длине отрезка АВ, изображающего вектор.

Определение: Вектор называется нулевым, если начало и конец вектора совпадают.

Определение: Вектор единичной длины называется единичным.

Определение: Векторы называются коллинеарными, если они лежат на одной прямой или на параллельных прямых ( || ).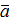

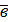Замечание:

1.Коллинеарные векторы могут быть направлены одинаково или противоположно.

2. Нулевой вектор считается коллинеарным любому вектору.

Определение: Два вектора называются равными, если они коллинеарные,

одинаково направлены и имеют одинаковые длины ( = )

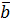Определение: Три вектора называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях

2. Линейные операции над векторами:

Произведением вектора 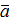на число λ называется вектор 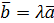, имеющий длину 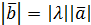, направление которого совпадает с направлением вектора 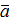, если λ>0, и противоположно ему, если λ<0

Противоположным вектором – называется произведение вектора на число (-1), т. е. – =(-1)

Суммой двух векторов и 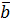называется вектор 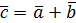, начало которого совпадает с началом вектора , а конец – с концом вектора 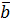, при условии, что начало вектора 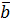совпадает с концом вектора (правило треугольников)

Сумму двух векторов можно построить также по правилу параллелограмма, где вектор 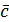представляет собой диагональ параллелограмма

Аналогично определяется сумма нескольких векторов.

Например, суммой четырех вектор 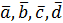является вектор 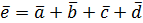, начало которого совпадает с началом вектора , а конец – с концом вектора 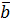(правило многоугольника)

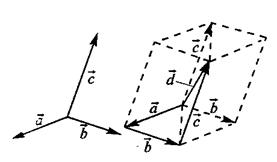
Вектор 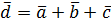, определяемый таким образом, представляет собой диагональ параллелепипеда, построенного на векторах 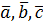, не лежащих в одной плоскости или в параллельных плоскостях (правило параллелепипеда)

Разностью двух векторов 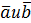называется сумма вектора и вектора 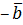, противоположного 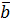(можно вычитать векторы по правилу 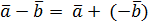, т. е. вычитание векторов заменить сложением вектора с вектором, противоположным вектору )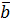

Замечание: в параллелограмме, построенном на векторах 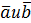, одна направленная диагональ является суммой этих векторов, а другая – разностью.

Определение: Координатами вектора 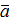называются координаты его конечной точки.

y

На плоскости Oxy координатами вектора являются числа x и y( (x, y)), а в пространстве Oxyz – три числа x, y, z ( (x, y, z))