Числовые характеристики непрерывной случайной величины.

Математическое ожидание непрерывной случайной величины X определяется равенством

M(X) =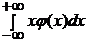

Дисперсия непрерывной случайной величины X определяется равенство D(X) =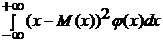

Модой M₀(X) случайной величины X называется ее наиболее вероятное значение (для которого вероятность P_i или плотность вероятности φ(x) достигает максимума).

Медианой M_e(X) непрерывной случайной величины X называется такое ее значение, для которого

P(X < M_e(X)) = P(X > M_e(X)) = .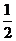

Начальным моментом k-ого порядка случайной величины X называется математическое ожидание k-ой степени этой величины:

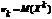.Если X – дискретная случайная величина, то 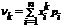Если X – непрерывная случайная величина, то 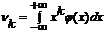Центральным моментом k-ого порядка случайной величины X называется величина

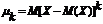и

Для дискретной величины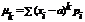

Для непрерывной величины

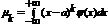
23.Плотность распределения вероятностей непрерывной случайной величины.

Как отмечалось в 3.3, функция распределения непрерывной случайной величины является непрерывной функцией. Кроме того, эта функция дифференцируема, за исключением, быть может, отдельных точек. Тогда для непрерывной случайной величины вероятность любого отдельно взятого значения x₀ равна нулю, т.е. P(X = x_0­) = 0 и

P(x₁ < X < x₂) = F(x₂) – F(x₁)

Таким образом, для непрерывной случайной величины вероятность попадания на интервал не зависит от того, является ли этот интервал открытым или закрытым.

Непрерывную случайную величину можно задать с помощью плотности вероятности.

Плотностью распределения вероятностей φ(x) непрерывной случайной величины X называют первую производную от функции F(x): φ(x) = F 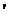(x)

Плотность φ(x) иногда называют дифференциальным законом распределения, а его график – кривой распределения.Плотность распределения вероятностей обладает следующими свойствами.

1. Это неотрицательная функция: φ(x) ≥ 0.

2. Вероятность попадания случайной величины на интервал (a;b) имеет вид

P(a < X < b) =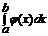

3. Функция распределения непрерывной случайной величины связана с плотностью вероятностей, а именно F(x) = 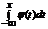= 1

4. Несобственный интеграл от плотности распределения φ(x) в пределах от - 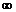до + 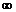равен единице: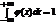

Из свойств плотности вероятностей следует, что ее график лежит не ниже оси абсцисс, а площадь фигуры, ограниченной кривой распределения и осью абсцисс, равна единице.

24. Равномерное распределение. Непрерывная величина Х распределена равномерно на интервале (a, b), если все ее возможные значения находятся на этом интервале и плотность распределения вероятностей постоянна:

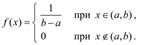
Для случайной величины Х , равномерно распределенной в интервале (a, b) (рис. 4), вероятность попадания в любой интервал (x1, x2), лежащий внутри интервала (a, b), равна:

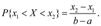
25. Показательное распределение. Непрерывная случайная величина Х имеет показательное распределение, если плотность распределения ее вероятностей выражается формулой:

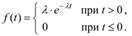
Время Т безотказной работы компьютерной системы есть случайная величина, имеющая показательное распределение с параметром λ , физический смысл которого – среднее число отказов в единицу времени, не считая простоев системы для ремонта.

26. Нормальное (гауссово) распределение. Случайная величина Х имеет нормальное (гауссово) распределение, если плотность распределения ее вероятностей определяется зависимостью:

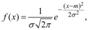где m = M(X) , .

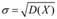При 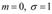нормальное распределение называется стандартным.Определение неизвестных параметров распределения.пусть x₁, x₂, ..., x_n - наблюдаемые значения непрерывной случайной величины 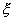, и пусть ее плотность распределения вероятностей зависит от двух неизвестных параметров A и B, т.е. имеет вид 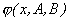. Один из методов нахождения неизвестных параметров A и B состоит в том, что их выбирают таким образом, чтобы математическое ожидание и дисперсия теоретического распределения совпали с выборочными средними значением 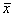и дисперсией :

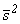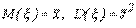где

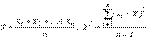(67)

Из двух полученных уравнений (66) находят неизвестные параметры A и B. Так, например, если случайная величина 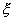подчиняется нормальному закону распределения вероятностей, то ее плотность распределения вероятностей

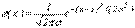зависит от двух параметров a и 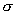. Эти параметры, как мы знаем, являются соответственно математическим ожиданием и средним квадратическим отклонением случайной величины 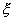; поэтому равенства (66) запишутся так:

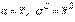(68)

Следовательно, плотность распределения вероятностей имеет вид

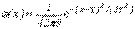
27. Правило трёх сигм

При рассмотрении нормального закона распределения выделяется важный частный случай, известный как правило трех сигм.Запишем вероятность того, что отклонение нормально распределенной случайной величины от математического ожидания меньше заданной величины D:Если принять D = 3s, то получаем с использованием таблиц значений функции Лапласа:Т.е. вероятность того, что случайная величина отклонится от своего математического ожидание на величину, большую чем утроенное среднее квадратичное отклонение, практически равна нулю.Это правило называется правилом трех сигм.

Стандартное отклонение (иногда среднеквадратичное отклонение) — показатель рассеивания значений случайной величины относительно еёматематического ожидания. .

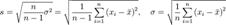
где — стандарт, стандартное отклонение, несмещенная оценка среднеквадратического отклоненияслучайной величины X относительно её математического ожидания; 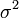— дисперсия; 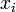— i-й элементвыборки; 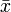— среднее арифметическое выборки; 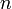— объём выборки.

Следует отметить отличие стандарта (в знаменателе n − 1) от корня из дисперсии(среднеквадратическогоотклонения)(в знаменателе n), при малом объёме выборки оценка дисперсии через последнюю величинуявляется несколько смещенной, при бесконечно большом объёме выборки разница между указаннымивеличинами исчезает. Выборка — лишь часть генеральной совокупности. Генеральная совокупность —абсолютно все возможные результаты. Правило 3-х сигм ( 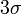) — практически все значения нормально распределённой случайной величины лежатв интервале 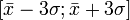. Более строго не менее чем с 99,7 % достоверностью, значениенормально распределенной случайной величины лежит в указанном интервале. При условии что величина 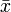истинная, а не полученная в результате обработки выборки. Если же истинная величина неизвестна, тоследует пользоваться не σ, а s. Таким образом, правило 3-х сигм преобразуется в правило трех s

28. Закон больших чисел в теории вероятностей утверждает, что эмпирическое среднее (среднее арифметическое) конечной выборки из фиксированного распределения близко к теоретическому среднему (математическому ожиданию) этого распределения. В зависимости от вида сходимости различают слабый закон больших чисел, когда имеет место сходимость по вероятности, и усиленный закон больших чисел, когда имеет место сходимость почти наверняка.Теоретическим обоснованием этого замечательного свойства случайных явлений является закон больших чисел. Названием "закон больших чисел" объединена группа теорем, устанавливающих устойчивость средних результатов большого количества случайных явлений и объясняющих причину этой устойчивости.Простейшая форма закона больших чисел, и исторически первая теорема этого раздела - теорема Бернулли, утверждающая, что если вероятность события одинакова во всех испытаниях, то с увеличением числа испытаний частота события стремится к вероятности события и перестает быть случайной.Теорема Пуассона утверждает, что частота события в серии независимых испытаний стремится к среднему арифметическому его вероятностей и перестает быть случайной.В основе качественных и количественных утверждений закона больших чисел лежит неравенство Чебышева. Оно определяет верхнюю границу вероятности того, что отклонение значения случайной величины от ее математического ожидания больше некоторого заданного числа. Замечательно, что неравенство Чебышева дает оценку вероятности события 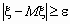для случайной величины, распределение которой неизвестно, известны лишь ее математическое ожидание и дисперсия.

Неравенство Чебышева. Если случайная величина x имеет дисперсию, то для любого e > 0 справедливо неравенство 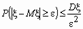, где Mx и Dx - математическое ожидание и дисперсия случайной величины x

.

29. Закон больших чисел (теорема Чебышева) теорему Чебышева. Эта теорема устанавливает связь между средним арифметическим наблюденных значений случайной величины и ее математическим ожиданием.Имеется случайная величина 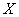с математическим ожиданием 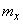и дисперсией 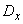. Над этой величиной производится 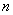независимых опытов и вычисляется среднее арифметическое всех наблюденных значений величины 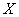. Требуется найти числовые характеристики этого среднего арифметического - математическое ожидание и дисперсию - и выяснить, как они изменяются с увеличением .

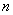Обозначим: 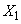- значение величины 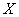в первом опыте;

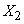- значение величины 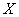во втором опыте, и т. д.

Очевидно, совокупность величин 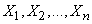представляет собой 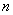независимых случайных величин, каждая из которых распределена по тому же закону, что и сама величина 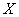. Рассмотрим среднее арифметическое этих величин:

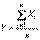.Случайная величина 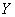есть линейная функция независимых случайных величин 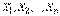. Найдем математическое ожидание и дисперсию этой величины. Согласно правилам 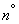10 для определении числовых характеристик линейных функций получим:

;

.

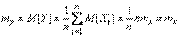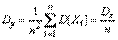Теорема Чебышева и устанавливает в точной количественной форме это свойство устойчивости среднего арифметического. Она формулируется следующим образом:

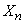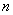Запишем теорему Чебышева в виде формулы. Для этого напомним смысл термина «сходится по вероятности». Говорят, что случайная величина сходится по вероятности к величине , если при увеличении вероятность того, что 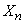и 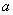будут сколь угодно близки, неограниченно приближается к единице, а это значит, что при достаточно большом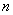

,

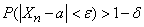где 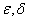- произвольно малые положительные числа.

Запишем в аналогичной форме теорему Чебышева. Она утверждает, что при увеличении 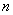среднее арифметическое 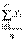сходится по вероятности к 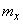, т. е.

.

Докажем это неравенство.

Доказательство. Выше было показано, что величина

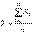имеет числовые характеристики

; .

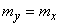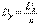Применим к случайной величине 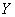неравенство Чебышева, полагая : .

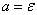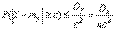Как бы мало ни было число 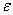, можно взять 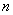таким большим, чтобы выполнялось неравенство

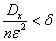где 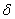- сколь угодно малое число.

Тогда ,откуда, переходя к противоположному событию, имеем: ,

что и требовалось доказать.

30. Закон больших чисел. Теорема бернулли

Закон больших чисел в форме Бернулли состоит в следующем: с вероятностью, сколь угодно близкой к единице, можно утверждать, что при достаточно большом числе опытов частота появления события А как угодно мало отличается от его вероятности, т. е.

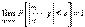иными словами, при неограниченном увеличении числа n опытов частота m/n события А сходится по вероятности к Р(А).

Доказательство:

Рассмотрим случайную величину 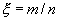. Так как M(m)=np и D(m)=npq то

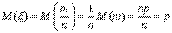
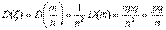
Применим к случайной величине 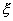вторую лемму Чебышева:

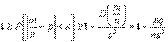
Переходя к пределу при 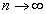, очевидно, имеем

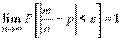
31 . Совместное рассмотрение двух или нескольких случайных величин приводит к понятию системы случайных величин. Условимся систему нескольких случайных величин 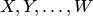обозначать 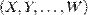. Такая система называется также многомерной случайной величиной. При рассмотрении системы случайных величин удобно пользоваться геометрической интерпретацией системы. Например, систему двух случайных величин 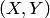можно рассматривать как случайную точку на плоскости 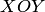с координатам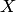и и 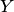или как случайный вектор на плоскости со случайными составляющим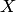и и 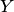. По аналогии систему 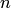случайных величин можно рассматривать как случайную точку в 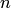-мерном пространстве или как n-мерный случайный вектор.При изучении систем случайных величин ограничимся подробным рассмотрением системы двух случайных величин.
Закон распределения вероятностей системы случайных величиЗаконом распределения системы случайных величин называется соотношение, устанавливающее связь между областями возможных значений системы случайных величин и вероятностями появления системы в этих областях.[/b]Так же, как и для одной случайной величины, закон распределения системы случайных величин может быть задан в различных формах. Рассмотрим таблицу распределения вероятностей системы дискретных случайных величин. 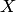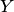Пусть и — дискретные случайные величины, возможные значения которых 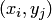, где 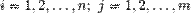Тогда распределение системы таких случайных величин может быть охарактеризовано указанием вероятностей 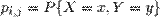того, что случайная величина 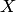примет значение 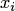и одновременно с этим случайная величина 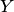примет значение 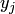. Вероятности 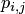фиксируют в таблицеТакая таблица называется таблицей распределения системы двух дискретных случайных величин с конечным числом возможных значений. Все возможные события 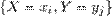при 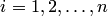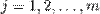составляют полную группу несовместных событий, поэтом

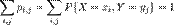
32. Понятие двумерной случайной величины и закон ее распределения.

Зачастую результат опыта описывается несколькими случайными величинами: 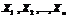.В этом случае говорят о многомерной случайной величине 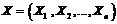или о системе случайных величин 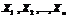.Рассмотрим двумерную случайную величину 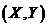, возможные значения которой есть пары чисел 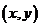. Геометрически двумерную случайную величину можно истолковать как случайную точку на плоскости 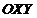.Если составляющие Х и Y – дискретные случайные величины, то 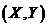- дискретная двумерная случайная величина, а если Х и Y – непрерывные, то 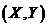- непрерывная двумерная случайная величина.Законом распределения вероятностей двумерной случайной величины называют соответствие между возможными значениями и их вероятностями.закон распределения двумерной дискретной случайной величины может быть задан в виде таблицы с двойным входом (см. таблица 6.1), где 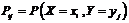- вероятность того, что составляющая Х приняла значение x_i, а составляющая Y – значение y_j.

33. Закон распределения двумерной случайной величины 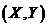можно задать в виде функции распределения 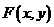, определяющей для каждой пары чисел 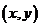вероятность того, что Х примет значение, меньшее х, и при этом Y примет значение, меньшее y:

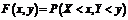. Геометрически функция 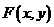означает вероятность попадания случайной точки 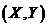в бесконечный квадрат с вершиной в точке 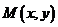Отметим свойства .

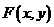1. Область значений функции 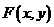- 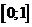, т.е. .

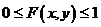2. Функция 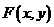- неубывающая функция по каждому аргументу.

3. Имеют место предельные соотношения:

; ; ; .

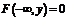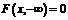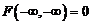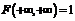При 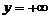функция распределения системы становится равной функции распределения составляющей Х, т.е.

Зная 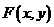, можно найти вероятность попадания случайной точки 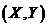в пределы прямоугольника ABCD

34.Для двумерной непрерывной случайной величины вводится понятие плотности вероятности

.

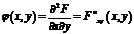Геометрическая плотность вероятности 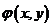представляет собой поверхность распределения в пространстве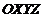

Двумерная плотность вероятности обладает следующими свойствами:

1.

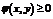
2.

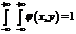
3. Функция распределения 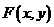может быть выражена через 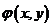по формуле

.

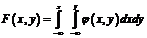4. Вероятность попадания непрерывной случайной величины 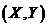в область 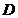равна

.

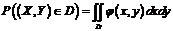5. В соответствии со свойством (4) функции 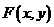имеют место формулы:

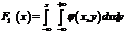
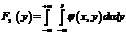
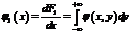(6.1.8)

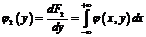
35. Условные законы распределения

По аналогии с условными вероятностями вводятся условные законы распределения составляющих непрерывной двумерной случайной величины 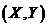, а именно

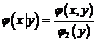- условная плотность распределения Х при заданном значении ;

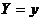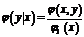- условная плотность распределения Y при заданном значении .

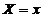Если случайные величины X и Y независимые, т.е. закон распределения каждой из них не зависит от того, какое значение принимает вторая величина, то условные и безусловные законы Х и Y совпадают. В частност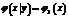и, и 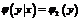. Таким образом, для независимых составляющих Х и Y двумерная плотность вероятности находится следующим образом 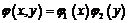и функция распределения 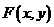имеет вид 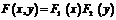. Если составляющие Х и Y дискретной случайной величины – независимые случайные величины, то

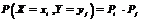, где , ,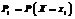

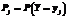36. Числовые характеристики двумерной случайной величины.

При изучении двумерных случайных величин рассматриваются числовые характеристики составляющих:

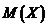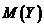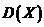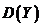, , , , где

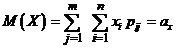
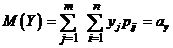
(6.2.1)

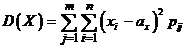
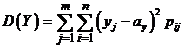для дискретных составляющих X и Y и

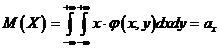
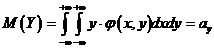
(6.2.2)

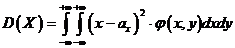
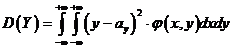в случае непрерывных составляющих.

Упорядоченную пару чисел 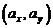называют математическим ожиданием двумерной случайной величины, а 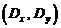- ее дисперсия.

Отмеченные выше числовые характеристики не определяют степень зависимости составляющих X и Y. Эту роль выполняют корреляционный момент 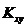(иначе: ковариация 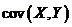), который определяется следующим образом:

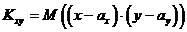. (6.2.3)

Для дискретных случайных величин

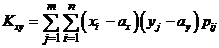(6.2.4)

Для непрерывных случайных величин

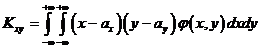(6.2.5)

Корреляционный момент можно вычислить по формуле (6.2.6)

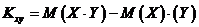. (6.2.6)

Если Х и Y независимы, то 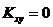. Если 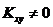, то Х и Y зависимые случайные величины.

В случае 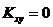случайные величины X и Y называют некоррелированными, при этом она могут быть как зависимыми, так и независимыми.

Ковариация X и Y характеризует не только степень зависимости случайных величин, но и их рассеяние вокруг точки 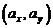. Кроме того, 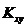- размерная величина, что затрудняет ее использование для оценки степени зависимости для различных случайных величин.

Для оценки зависимости вводится коэффициент корреляции

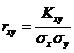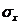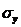, (6.2.7) где и - среднеквадратические отклонения X и Y.

Коэффициент корреляции 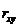- безразмерная величина, обладающая следующими свойствами:

1. 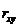- ограниченная величина, а именно .

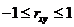2. Если X и Y – независимые случайные величины, то .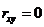

3. Если X и Y связаны линейной функциональной зависимостью 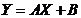, то 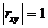и наоборот.

Из последнего свойства можно сделать вывод: коэффициент корреляции характеризует степень линейной зависимости случайных величин X и Y.

37/ Условным математическим ожиданиемдискретной случайной величины Y при X = x (х – определенное возможное значение Х) называется произведение всех возможных значений Y на их условные вероятности.Для непрерывных случайных величин:

где f(y/x) – условная плотность случайной величины Y при X=x.Условное математическое ожидание M(Y/x)=f(x) является функцией от х и называется функцией регрессии Х на Y

38. Зависимые и независимые случайные величины. Корреляция

Определение. Случайная величина X называется независимойот случайной величины Y если закон распределения X не зависит от того, какие значения приняла Y.Можно показать, что в этом случае и Y не зависит от X, поэтому такие случайные величины часто называют независимымиТеорема. Случайные величины X и Y независимы тогда и только тогда, когда 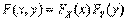.Доказательство.Необходимость. Пусть X и Y независимы, а, значит, события X < x и Y < y — независимы. Тогда для вероятности произведения независимых событий имеем 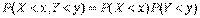, что и доказывает первое утверждение теоремы.. Определение. Корреляционным моментом 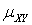случайных величин X и Y называют 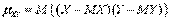.Если X = Y, то есть если понятие корреляционного момента применить для двух одинаковых случайных величин, то это будет ни что иное, как дисперсия. Формулу, записанную в определении, можно преобразовать к виду: 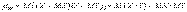.В явном виде корреляционный момент запишется как: 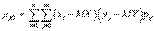— для дискретных случайных величин; 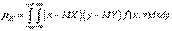— для непрерывных случайных величин.Теорема. Если случайные величины X и Yнезависимы, то их корреляционный момент 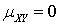.Доказательство.Если X и Yнезависимы, то случайные величины X - MX и Y - MY тоже независимы. Тогда, используя свойства математического ожидания, получаем: 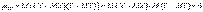.Теорема доказана.Если случайные величины X и Yимеют размерность, то корреляционный момент также будет иметь размерность, равную произведению размерностей каждой из величин X и Y. Часто используют другую характеристику взаимосвязи двух случайных величин, называемую коэффициент корреляции.Определение. Коэффициентом корреляции 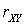случайных величин X и Y называют отношение корреляционного момента к произведению дисперсий каждой из случайных величин: 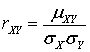.Определенный таким образом коэффициент корреляции оказывается всегда безразмерным и, таким образом не зависит от выбора системы единиц при измерении случайных величин. Очевидно, что доказанная выше теорема справедлива и для коэффициента корреляции.Теорема. Для корреляционного момента справедливо неравенство 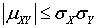.Доказательство.Рассмотрим случайную величину 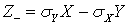и, используя свойства математического ожидания, вычислим дисперсию: 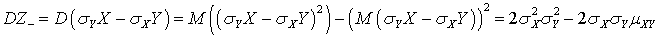.Учитывая, что дисперсия всегда не отрицательна 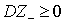, получаем неравенство 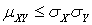. Аналогичным образом рассматривая случайную величину 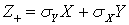, можно получить, что 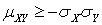. Объединяя эти два неравенства, получаем 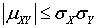, что и доказывает теорему.Следствие. Для коэффициента корреляции справедливо неравенство 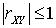.Доказательство. Очевидно из определения коэффициента корреляции.Определение. Случайные величины X и Yназывают коррелированными , если их корреляционный момент (а, значит, и коэффициент корреляции) не равен нулю. Случайные величины X и Yназывают некоррелированными , если их корреляционный момент (а, значит, и коэффициент корреляции) равен нулю.Здесь следует обратить внимание на неэквивалентность понятий зависимости — независимости и коррелированности — некоррелированности. Две коррелированные случайные величины зависимы, а две независимые случайные величины — не коррелированны. Второе из этих утверждений было доказано выше в одной из теорем, а первое утверждение можно доказать, предполагая противное, то есть если коррелированные величины независимы, то тогда их корреляционный момент был бы равен нулю, а, значит, они были бы не коррелированны. Значит, наше предположение неверно, что и доказывает первое утверждение. Напротив, зависимые случайные величины могут быть коррелированными (это очевидно, так как коррелированные величины зависимы), а могут и не быть таковыми.

39. Ковариация оценивает силу линейной зависимости между двумя числовыми переменными X и Y. Выборочная ковариация:

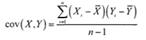
Любопытно, что ковариация случайной величины с собой равна дисперсии:Если ковариация положительна, то с ростом значений одной случайной величины, значения второй имеют тенденцию возрастать, а если знак отрицательный — то убывать. Однако только по абсолютному значению ковариации нельзя судить о том, насколько сильно величины взаимосвязаны, так как её масштаб зависит от их дисперсий. Масштаб можно отнормировать, поделив значение ковариации на произведение среднеквадратических отклонений (квадратных корней из дисперсий). При этом получается так называемый коэффициент корреляции Пирсона.

Относительная сила зависимости, или связи, между двумя переменными, образующими двумерную выборку, измеряется коэффициентом корреляции, изменяющимся от –1 для идеальной обратной зависимости до +1 для идеальной прямой зависимости. Коэффициент корреляции обозначается греческой буквой ρ. Линейность корреляции означает, что все точки, изображенные на диаграмме разброса, лежат на прямой

При анализе выборок, содержащих двумерные данные, вычисляется выборочный коэффициент корреляции, который обозначается буквой r. В реальных ситуациях коэффициент корреляции редко принимает точные значения -1, 0 и +1. На рис. 3 приведены шесть диаграмм разброса и соответствующие коэффициенты корреляции rмежду 100 значениями переменных X и Y.

ыборочный коэффициент корреляции:

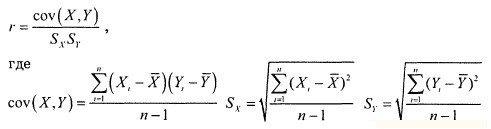
Ковариация представляет собой математическое ожидание произведения центрированных случайных величин X иY и характеризует степень линейной статистической зависимости велич