Числовые характеристики непрерывной случайной величины

Математическим ожиданием непрерывной случайной величины X, возможные значения которой принадлежат интервалу (a, b), называют определенный интеграл:

M(X) ₌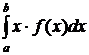

Дисперсия непрерывной случайной величины X, возможные значения которой принадлежат интервалу (a,b), определятся равенством:

D(Х) = .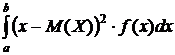

При решении задач более удобно использовать следующие формулы для вычисления дисперсии:

D(Х) = .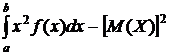

Среднее квадратическое отклонение непрерывной случайной величины определяется, как и для дискретной величины, равенством:

.

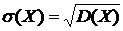Основные понятия математической статистики

Математическая статистика разрабатывает способы сбора, группировки и анализа статистических данных, то есть сведений, получен­ных в результате многократных наблюдений за изучаемым явлением. Методы математической статистики позволяют решать многие задачи, которые возникают на практике.

В процессе статистического наблюдения обследованию могут подвергаться как все элементы данной совокупности объектов, так и ее часть. В соответствии с этим различают сплошные наблюдения и несплошные. Наиболее совершенный и научно обоснованный метод несплошных наблюдений − это выборочное наблюдение. Оно позволяет на основе обследования некоторой части совокупности судить совокупности в целом.

В связи с этим выборочной совокупностью, или простовыборкой, называют совокупность случайно отобранных объектов.

Вся совокупность объектов, из которых производится выборка, называется генеральнойсовокупностью.

Объемом совокупности называется число объектов данной совокупности.

Для того, чтобы по данным выборки можно было судить с достаточной уверенностью об интересующем признаке генеральной совокупности необходимовыполнение требования репрезентативности (представительности), то есть выборка должна правильно представлять пропорции генеральной совокупности. Для выполнения этого требования необходимо, чтобы каждый объект выборки отбирался случайно из генеральной совокупности и чтобы все объекты имели одинаковую вероятность попасть в выборку.

Рассмотрим выборку объемом n. Пусть значение x₁исследуемого признака Х наблюдалось n₁ раз, x₂ − n₂ раза, x_k − n_k раз.

Наблюдаемые значения x_i называют вариантами,а последовательность вариант,записанных в порядке возрастания − вариационным рядом. Числа наблюдений n_i называют частотами, а их отношение к объему выборки n_i /n =w_i − относительными частотами.

Статистическим распределением выборки называют перечень вари­ант и соответствующих им частот или относительных частот. Сумма всех относительных частот равна единице.

Статистическое распределение можно задать также в виде последовательности интервалов и соответствующих им частот. В качестве частоты, соответствующей интервалу, принимают сумму частот, попавших в этот интервал.

Эмпирической функцией распределения (или функцией распределения выборки) называют функцию F^*(x), определяющую для каждого значения x относительную частоту события X < х, то есть

F^*(x) = n_x/n,

где n_x − число вариант, меньших х; n − объем выборки.

В отличии от эмпирической функции распределения выборки функцию распределения F(x) генеральной совокупности называют теоретической функцией распределения.

Различие между теоретической и эмпирической функциями распределения заключается в том, что теоретическая функция F(x) показывает вероятность события Х < х, а эмпирическая функция F^*(x) определяет относительную частоту этого же события.

Для наглядного представления статистического распределения выборки строят различные графики (полигоны и гистограммы).

При дискретном распределении признака Х строят полигоны частот или полигоны относительных частот.

Полигоном частот называют ломаную линию, отрезки которой соединяют точки (x₁, n₁), (x₂, n₂), ..., (x_k, n_k), где x_i − варианты выборки, n_i − соответствующие им частоты.

Полигоном относительных частот называют ломаную линию, отрезки которой соединяют точки (x₁, w₁), (x₂, w₂), ..., (x_k, w_k), где x_i − варианты выборки, w_i − соответствующие им относительные частоты.

При непрерывном распределении признака Х весь интервал, в котором заключены все наблюдаемые значения признака, разбивают на ряд частичных интервалов длиной h и находят n_i − сумму частот вариант, попавших в i-й интервал.

Гистограммой частот называется ступенчатая фигура, состоящая из прямоугольников, основаниями которых служат частичные интервалы длиной h, а высоты равны отношению n_i/h (плотность частоты).

Площадь частичного интервала i-го прямоугольника равна (h × n_i) / h = n_i − сумме частот вариант, попавших в i-й интервал. Следовательно, площадь всей гистограммы равна сумме всех частот, то есть объему выборки.

Гистограммой относительных частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы h, а высоты равны отношению w_i/h, то есть плотности относительной частоты.

Площадь гистограммы относительных частот равна сумме всех относительных частот, которая равна единице.