Элементы векторной алгебры, аналитической геометрии и линейной алгебры
Тематика контрольных работ
Контрольная работа № 1содержит 5 задач по темам: векторная алгебры, аналитическая геометрия и линейная алгебра.
Контрольная работа № 2содержит 5 задач по темам: введение в математический анализ, производная и ее приложения.
Контрольная работа № 3содержит 4 задачи по темам: неопределенный и определенный интегралы.
Контрольная работа № 4содержит 4 задач по темам: функции нескольких переменных, элементы теории векторных полей.
Контрольная работа № 5 содержит 7 задач по темам: дифференциальные уравнения и системы, ряды, операционный метод,
Контрольная работа № 6 содержит 6 задач по темам: теория вероятностей и элементы массового обслуживания, математическая статистика.
Задание на контрольные работы и общие указания к их выполнению
Работы выполняются и оформляются в соответствии с требованиями, предъявляемыми к контрольным работам.
Контрольная работа №1
Элементы векторной алгебры, аналитической геометрии и линейной алгебры
Задача 1.1
Даны координаты вершин пирамиды А1, А2, А3, А4. Найти площадь грани А1А2А3 и объем пирамиды. Сделать чертеж. Сделать проверку решения в MathCad.
Варианты заданий к задаче 1.1:
11. А1 (4; 2; 5), А2 (0; 7; 2), А3 (0; 2; 7), А4 (1; 5; 0) .
12. А1 (4; 4; 10), А2 (4; 10; 2), А3 (2; 8; 4), А4 (9; 6; 4) .
13. А1 (4; 6; 5), А2 (6; 9; 4), А3 (2; 10; 10), А4 (7; 5; 9) .
14. А1 (3; 5; 4), А2 (8; 7; 4), А3 (5; 10; 4), А4 (4; 7; 8) .
15. А1 (10; 6; 6), А2 (-2; 8; 2), А3 (6; 8; 9), А4 (7; 10; 3) .
16. А1 (1; 8; 2), А2 (5; 2; 6), А3 (5; 7; 4), А4 (4; 10; 9) .
17. А1 (6; 6; 5), А2 (4; 9; 5), А3 (4; 6; 11), А4 (6; 9; 3) .
18. А1 (7; 2; 2), А2 (5; 7; 7), А3 (5; 3; 1), А4 (2; 3; 7) .
19. А1 (8; 6; 4), А2 (10; 5; 5), А3 (5; 6; 8), А4 (8; 10; 7) .
20. А1 (7; 7; 3), А2 (6; 5; 8), А3 (3; 5; 8), А4 (8; 4; 1) .
Задача 1.2
Составить уравнение прямой по заданным условиям задачи согласно варианту. Выполнить чертеж, иллюстрирующий решение. Сделать проверку решения в MathCad.
Варианты заданий к задаче 1.2:
21. Составить уравнение перпендикуляра, проходящего через середину отрезка 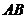 , если
, если 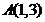 ;
; 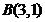 .
.
22. Составить уравнение прямой, проходящей через т. 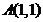 параллельно прямой
параллельно прямой 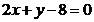 .
.
23. Составить уравнение прямой, проходящей через т. 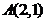 перпендикулярно прямой
перпендикулярно прямой 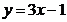 .
.
24. Составить уравнение перпендикуляра, проходящей через середину отрезка 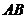 , если
, если 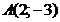 ;
; 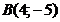 .
.
25. Составить уравнение прямой, проходящей через т. 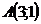 и параллельной прямой
и параллельной прямой 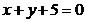 .
.
26. Составить уравнение прямой, проходящей через т. 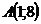 и параллельной прямой
и параллельной прямой 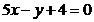 . Сделать чертеж.
. Сделать чертеж.
27. Составить уравнение перпендикуляра, проходящего через середину отрезка 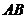 , если
, если 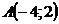 ;
; 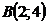 . Сделать чертеж.
. Сделать чертеж.
28. Составить уравнение прямой, проходящей через т. 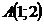 и параллельной прямой
и параллельной прямой 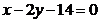 . Сделать чертеж.
. Сделать чертеж.
29. Составить уравнение прямой, проходящей через т. 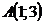 и перпендикулярной к прямой
и перпендикулярной к прямой 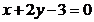 . Сделать чертеж.
. Сделать чертеж.
30. Составить уравнение перпендикуляра, проходящего через середину отрезка 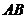 , если
, если 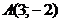 ;
; 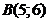 . Сделать чертеж.
. Сделать чертеж.
Задача 1.3
Решить задачу и выполнить чертеж. Сделать проверку решения в MathCad.
Варианты заданий к задаче 1.3:
31. Составить уравнения прямой, проходящей через т. 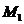
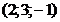 и
и 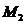
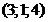 и указать какая из т.
и указать какая из т. 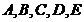 лежит на этой прямой:
лежит на этой прямой:
а) 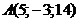 ; б)
; б) 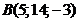 ; в)
; в) 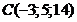 ; г)
; г) 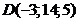 ;
;
д) 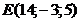 . Сделать чертеж.
. Сделать чертеж.
32. Составить уравнения прямой, проходящей через т. 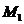
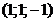 и
и 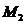
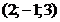 и указать какая из т.
и указать какая из т. 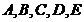 лежит на этой прямой:
лежит на этой прямой:
а) 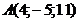 ; б)
; б) 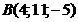 ; в)
; в) 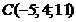 ; г)
; г) 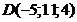 ;
;
д) 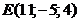 . Сделать чертеж.
. Сделать чертеж.
33. Составить уравнения прямой, проходящей через т. 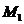
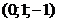 и
и 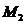
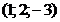 и указать какая из т.
и указать какая из т. 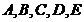 лежит на этой прямой:
лежит на этой прямой:
а) 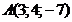 ; б)
; б) 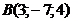 ; в)
; в) 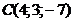 ; г)
; г) 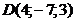 ;
;
д) 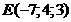 . Сделать чертеж.
. Сделать чертеж.
34. Составить уравнения прямой, проходящей через т. 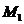
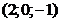 и
и 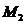
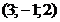 и указать какая из т.
и указать какая из т. 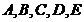 лежит на этой прямой:
лежит на этой прямой:
а) 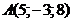 ; б)
; б) 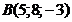 ; в)
; в) 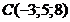 ; г)
; г) 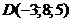 ;
;
д) 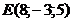 . Сделать чертеж.
. Сделать чертеж.
35. Составить уравнения прямой, проходящей через т. 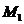
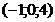 и
и 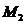
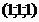 и указать какая из т.
и указать какая из т. 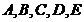 лежит на этой прямой
лежит на этой прямой
а) 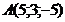 ; б)
; б) 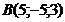 ; в)
; в) 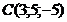 ; г)
; г) 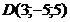 ;
;
д) 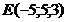 . Сделать чертеж.
. Сделать чертеж.
36. Составить уравнения прямой, проходящей через т. 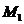
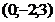 и
и 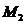
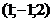 и указать какая из т.
и указать какая из т. 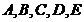 лежит на этой прямой
лежит на этой прямой
а) 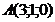 ; б)
; б) 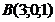 ; в)
; в) 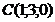 ; г)
; г)  ; д)
; д) 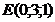 . Сделать чертеж.
. Сделать чертеж.
37. Составить уравнения прямой, проходящей через т. 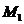
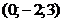 и
и 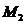
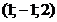 и указать какая из т.
и указать какая из т. 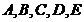 лежит на этой прямой
лежит на этой прямой
а) 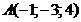 ; б)
; б) 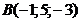 ; в)
; в) 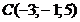 ; г)
; г) 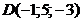 ; д)
; д) 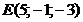 . Сделать чертеж.
. Сделать чертеж.
38. Составить уравнения прямой, проходящей через т. 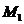
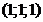 и
и 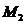
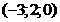 и указать какая из т.
и указать какая из т. 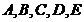 лежит на этой прямой
лежит на этой прямой
а) 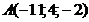 ; б)
; б) 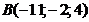 ; в)
; в) 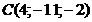 ; г)
; г) 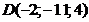 ; д)
; д) 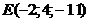 . Сделать чертеж.
. Сделать чертеж.
39. Составить уравнения прямой, проходящей через т. 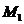
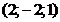 и
и 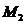
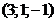 и указать какая из т.
и указать какая из т. 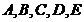 лежит на этой прямой
лежит на этой прямой
а) 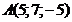 ; б)
; б) 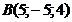 ; в)
; в) 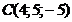 ; г)
; г) 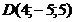 ;
;
д) 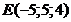 . Сделать чертеж.
. Сделать чертеж.
40. Составить уравнения прямой, проходящей через т. 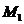
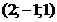 и
и 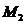
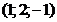 и указать какая из т.
и указать какая из т. 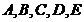 лежит на этой прямой
лежит на этой прямой
а) 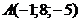 ; б)
; б) 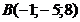 ; в)
; в) 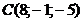 ; г)
; г) 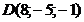 ; д)
; д) 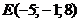 . Сделать чертеж.
. Сделать чертеж.
Задача 1.4
Варианты заданий к задаче 1.4
41. Составить уравнение и построить линию, расстояния каждой точки которой от начала координат и от точки А(5; 0) относятся как 2:1. Сделать чертеж.
42. Составитьуравнение и построить линию, расстояние каждой точки которой от точки А(–1; 0) вдвое меньше расстояния ее от прямой х=–4. Сделать чертеж.
43. Составить уравнение и построить линию, расстояния каждой точки которой от точки А(2; 0) и от прямой 5х+8=0 относятся, как 5:4. Сделать чертеж.
44. Составить уравнение и построить линию, каждая точка которой находится вдвое дальше от точки А(4; 0), чем от точки В(1; 0). Сделать чертеж.
45. Составить уравнение и построить линию, расстояния каждой точки которой от точки А(2; 0) и от прямой 2х+5=0 относятся, как 4:5. Сделать чертеж.
46. Составить уравнение и построить линию, расстояние каждой точки которой от точки А(3; 0) вдвое меньше расстояния от точки В(26; 0). Сделать чертеж.
47. Составить уравнение и построить линию, каждая точка которой одинаково удалена от точки А(0; 2) и от прямой у–4=0. Сделать чертеж.
48. Составить уравнение и построить линию, каждая точка которой равноотстоит от оси ординат и от окружности х2+у2=4х. Сделать чертеж.
Замечание. Напомним, что за расстояние от точки А до фигуры Ф принимается наименьшее из расстояний между точкой А и точками
фигуры Ф.
49. Составить уравнение и построить линию, каждая точка которой равноудалена от точки А(2; 6) и от прямой у+2=0. Сделать чертеж.
50. Составить уравнение и построить линию, каждая точка которой отстоит от точки А(–4; 0) втрое дальше, чем от начала координат. Сделать чертеж.
Задача 1.5
Систему линейных уравнений решить матричным методом, методом Крамера и методом Гаусса (методом исключения неизвестных). Сделать проверку.
Варианты системы линейных уравнений к задаче 1.5
51. 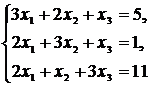 52.
52. 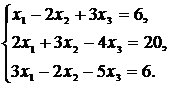
53. 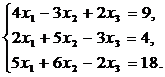 54.
54. 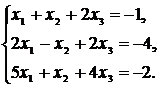
55. 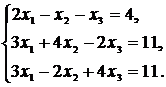 56.
56. 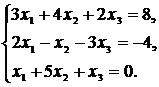
57. 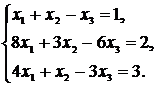 58.
58. 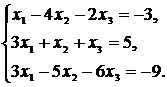
59. 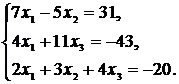 60.
60. 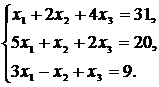
Контрольная работа №2
Задача 2.1
Найти пределы функций, не пользуясь правилом Лопиталя.
Варианты к задаче 2.1
61. а) 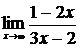 , б)
, б) 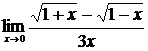 ,
,
в) 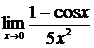 , г)
, г) 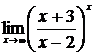
62. а) 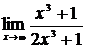 , б)
, б) 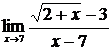 ,
,
в) 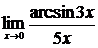 , г)
, г) 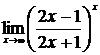
63. а) 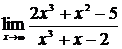 , б)
, б) 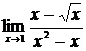 ,
,
в) 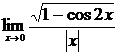 , г)
, г) 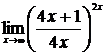
64. а) 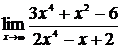 , б)
, б) 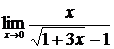 ,
,
в) 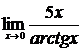 , г)
, г) 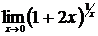
65. а) 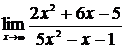 , б)
, б) 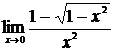 ,
,
в) 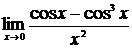 , г)
, г) 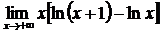
66. а) 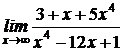 , б)
, б) 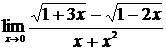
в) 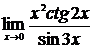 , г)
, г) 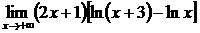
67. а) 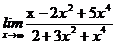 , б)
, б) 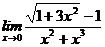
в) 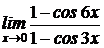 , г)
, г) 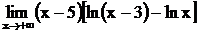
68. а) 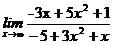 , б)
, б) 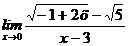
в) 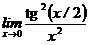 , г)
, г) 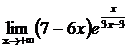
69. а) 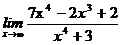 , б)
, б) 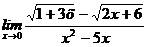
в) 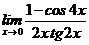 , г)
, г) 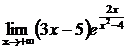
70. а) 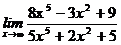 , б)
, б) 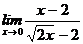
в) 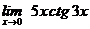 , г)
, г) 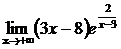 .
.
Задача 2.2
Задана функция у=f (х). Найти точки разрыва функции, если они существуют. Сделать схематический чертеж. Решение проверить в MathCad.
Варианты к задаче 1.7
71. 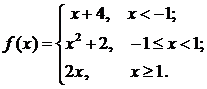 72.
72. 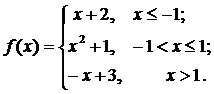
73. 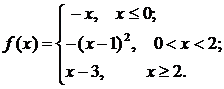 74.
74. 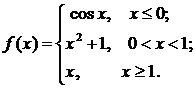
75. 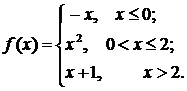 76.
76. 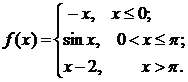
77. 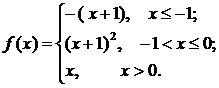 78.
78. 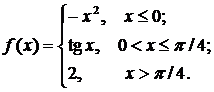
79. 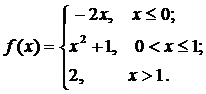 80.
80. 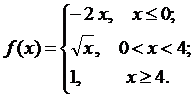
Задача 2.3
Найти производные 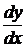 данных функций. Решение проверить в MathCad.
данных функций. Решение проверить в MathCad.
81. a) 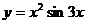 ; б)
; б) 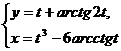 при
при 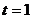 ; в)
; в) 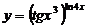 .
.
82. a) 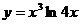 ; б)
; б) 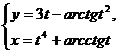 при
при 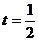 ; в)
; в) 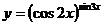 .
.
83. a) 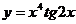 ; б)
; б) 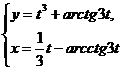 при
при 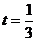 ; в)
; в) 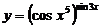 .
.
84. a) 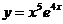 ; б)
; б) 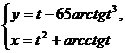 при
при 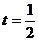 ; в)
; в) 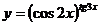 .
.
85. a) 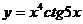 ; б)
; б) 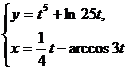 при
при 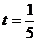 ;
;
в) 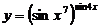 .
.
86. a) 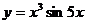 ; б)
; б) 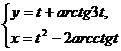 при
при 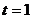 ;
;
в) 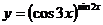 .
.
87. a) 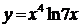 ; б)
; б) 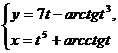 при
при 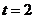 ;
;
в) 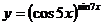 .
.
88. a) 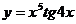 ; б)
; б) 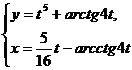 при
при 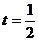 ;
;
в) 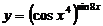 .
.
89. a) 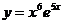 ; б)
; б) 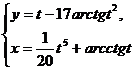 при
при 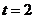 ;
;
в) 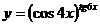 .
.
90. a) 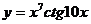 ; б)
; б) 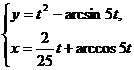 при
при 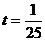 ;
;
в) 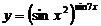 .
.
Задача 2.4
Найти пределы функции, применяя правило Лопиталя. Решение проверить в MathCad.


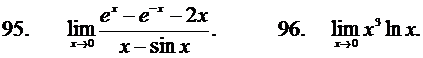
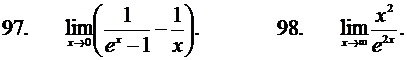

Задача 2.5.
Найти наибольшее и наименьшее значения функции 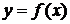 на отрезке
на отрезке 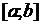 . Решение проверить в MathCad.
. Решение проверить в MathCad.
101. 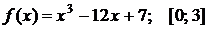 . 102.
. 102. 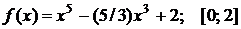 .
.
103. 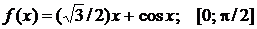 . 104.
. 104. 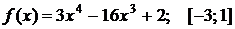 .
.
105. 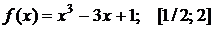 . 106.
. 106. 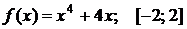 .
.
107. 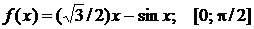 . 108.
. 108. 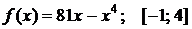 .
.
109. 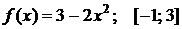 . 110.
. 110. 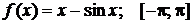 .
.
Контрольная работа №3
Задача 3.1
Найти неопределенные интегралы. В п. а) и б) результаты проверить дифференцированием. Решение проверить в MathCad.
111.а) 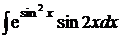 ; б)
; б) 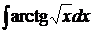 ;
;
в) 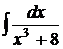 ; г)
; г) 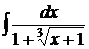 .
.
112.а) 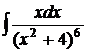 ; б)
; б) 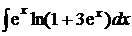 ;
;
в) 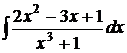 ; г)
; г) 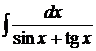 .
.
113. а) 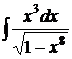 ; б)
; б) 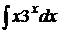 ;
;
в) 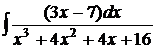 ; г)
; г) 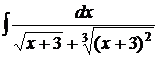 .
.
114.а) 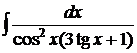 ; б)
; б) 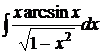 ;
;
в) 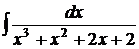 ; г)
; г) 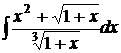 .
.
115.а) 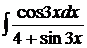 ; б)
; б) 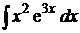 ;
;
в) 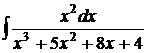 ; г)
; г) 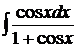 .
.
116.а) 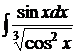 ; б)
; б) 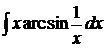 ;
;
в) 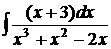 ; г)
; г) 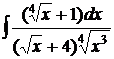 .
.
117.а) 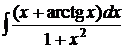 ; б)
; б) 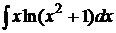 ;
;
в) 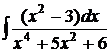 ; г)
; г) 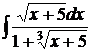 .
.
118.а) 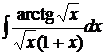 ; б)
; б) 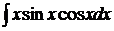 ;
;
в) 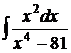 ; г)
; г) 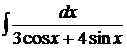 .
.
119.а) 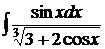 ; б)
; б) 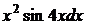 ;
;
в) 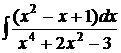 ; г)
; г) 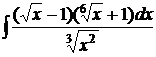 .
.
120.а) 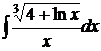 ; б)
; б) 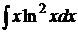 ;
;
в) 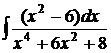 ; г)
; г) 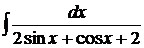 .
.
Задача 3.2
Вычислить определенные интегралы. Решение проверить в MathCad.
121. 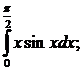 122.
122. 
123. 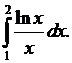 124.
124. 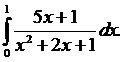
125. 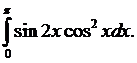 126.
126. 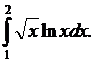
127. 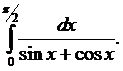 128.
128. 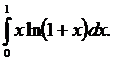
129. 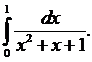 130.
130. 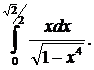
Задача 3.3
Решить указанныезадачи с помощью определенного интеграла. Решение проверить в MathCad.
131.Вычислить площадь фигуры, ограниченной параболой у=3х2+1 и прямой у=3х+7.
132.Вычислить площадь фигуры, ограниченной одной аркой цик-лоиды х=а(t–sin t), у=а(1–соs t)(0 ≤ t ≤ 2π) и осью Ох.
133.Вычислить площадь фигуры, ограниченной кардиоидой
r= 3(1+соs φ).
134.Вычислить площадь фигуры, ограниченной четырехлепестковой розой r=4sin 2φ.
135.Вычислить объем тела, образованного вращением вокруг оси Ох фигуры, ограниченной параболами у=х2 и у= 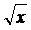 .
.
136.Вычислить объем тела, образованного вращением вокруг оси Ох фигуры, ограниченной полуэллипсом у=3 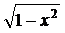 ,параболой х=
,параболой х= 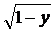 и осью Оу.
и осью Оу.
137.Вычислить объем тела, образованного вращением вокруг оси Оу фигуры, ограниченной кривыми y=2/(1+х2) и у=х2.
138.Вычислить длину дуги полукубической параболы y= 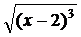 от точки A(2; 0) до точки B(6; 8).
от точки A(2; 0) до точки B(6; 8).
139.Вычислить длину кардиоиды r=3(1–соs φ).
140.Вычислить длину одной арки циклоиды х=3(t–sin t), у=3(1–соs t)(0 ≤ t ≤ 2π).
Задача 3.4
Разложить функцию f(x) в ряд Фурье в указанном интервале. Выписать полученный ряд и три первых члена разложения отдельно. Построить графики функции f(x) и ее приближения. Решение проверить в MathCad.
161. f(x) = x–1 в интервале 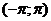 .
.
162. f(x) = x 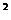 в интервале
в интервале 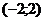 .
.
163. f(x) = 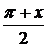 в интервале
в интервале 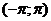 .
.
164. f(x) = 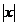 –1 в интервале
–1 в интервале 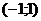 .
.
165. f(x) = 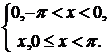 в интервале
в интервале 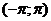 .
.
166. f(x) = 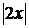 в интервале
в интервале 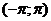 .
.
167. f(x) =|x|+2 в интервале 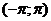 .
.
168. f(x) = x–3 в интервале 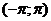 .
.
169. f(x) = x 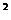 –1 в интервале
–1 в интервале 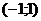 .
.
170. f(x) = 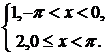 в интервале
в интервале 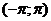 .
.
Контрольная работа №4
Задача 4.2.
Вычислить двойной интеграл. Решение проверить в MathCad.
151. 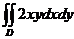 ; где область D – прямоугольник
; где область D – прямоугольник 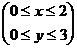 .
.
152.  ; где область D ограничена параболой
; где область D ограничена параболой 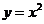 и прямыми
и прямыми 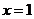 ,
, 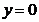 .
.
153.  ; где область D – прямоугольник
; где область D – прямоугольник 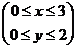 .
.
154. 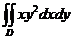 ; где область D – прямоугольник
; где область D – прямоугольник 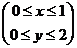 .
.
155. 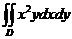 ; где область D – прямоугольник
; где область D – прямоугольник 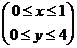 .
.
156. 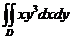 ; где область D – прямоугольник
; где область D – прямоугольник 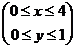 .
.
157. 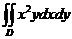 ; где область D ограничена параболой
; где область D ограничена параболой 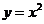 и прямыми
и прямыми 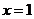 ,
, 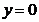 .
.
158. 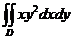 ; где область D ограничена параболой
; где область D ограничена параболой 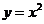 и прямыми
и прямыми 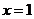 ,
, 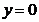 .
.
159. 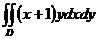 ; где область D – прямоугольник
; где область D – прямоугольник 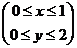 .
.
160. 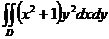 ; где область D – прямоугольник
; где область D – прямоугольник 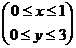 .
.
Задача 4.3
Найти поток векторного поля 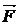 в направлении нормали
в направлении нормали 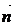 через поверхность S треугольника, высекаемого координатными плоскостями из плоскости, проходящей через точку P перпендикулярно вектору
через поверхность S треугольника, высекаемого координатными плоскостями из плоскости, проходящей через точку P перпендикулярно вектору 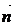 . Сделать чертеж. Решение проверить в MathCad.
. Сделать чертеж. Решение проверить в MathCad.
171. 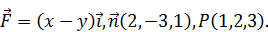
172. 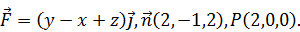
173. 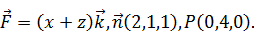
174. 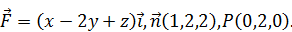
175. 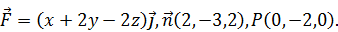
176. 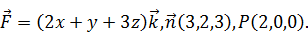
177. 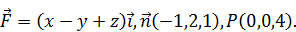
178. 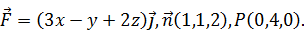
179. 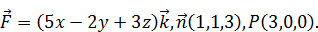
180. 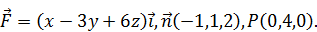
Задача 4.4
Проверить, является ли векторное поле 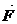 потенциальным или соленоидальным. В случае потенциальности поля
потенциальным или соленоидальным. В случае потенциальности поля 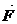 найти его потенциал. Решение проверить в MathCad.
найти его потенциал. Решение проверить в MathCad.
181. 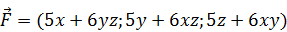 .
.
182. 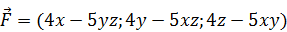 .
.
183. 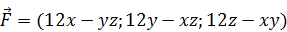 .
.
184. 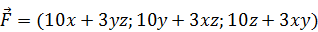 .
.
185. 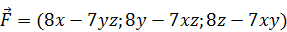 .
.
186. 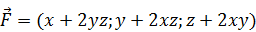 .
.
187. 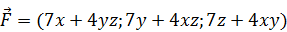 .
.
188. 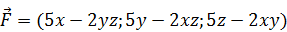 .
.
189. 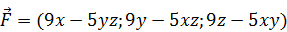 .
.
190. 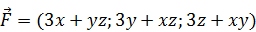 .
.
Контрольная работа №5
Дифференциальные уравнения и системы. Ряды. Операционный метод.
Задача 5.1
Найти решения дифференциальных уравнений первого порядка, удовлетворяющие указанным начальным условиям. Сделать проверку. Решение проверить в MathCad.
191. 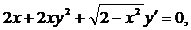 у(1) = 0.
у(1) = 0.
192. xy| + xey/x – y = 0, y(1) = 1 .
193. 20xdx – 3ydy = 3x2ydy – 5xy2dx, y(1) = 1.
194. xy | = y ln (y/x), y(1) = e.
195. 3(x2y + y)dy + 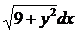 = 0, y(0) = 0.
= 0, y(0) = 0.
196. xy| + y = x + 1, y(1) = 0.
197. y| cosx = (y + 1)sinx, y(0) = 0.
198. xy| – y = 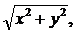 y(1) = 0.
y(1) = 0.
199. y| – y/x = x2, y(1) = 0.
200. y| + ycosx = 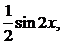 y(0) = 0.
y(0) = 0.
Задача 5.2
Решить дифференциальные уравнения второго порядка: а) найти общее решение; б) найти решение, удовлетворяющее указанным начальным условиям. Сделать проверку подстановкой ршения в исходное уравнение. Сделать проверить в MathCad аналитически и численно.
201. а) 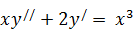 .
.
б) 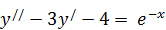 .
. 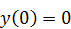 ,
, 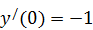 .
.
202. а) 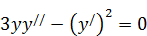 .
.
б) 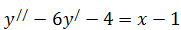 .
. 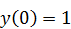 ,
, 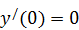 .
.
203. а) 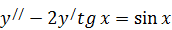 .
.
б) 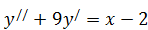 .
. 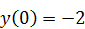 ,
, 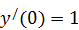 .
.
204. а) 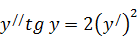
б) 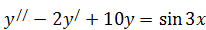 .
. 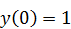 ,
, 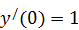 .
.
205. a) 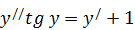
б) 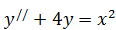 .
. 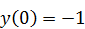 ,
, 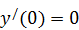 .
.
206. а) 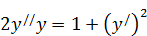
б) 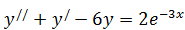 .
. 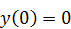 ,
, 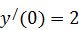 .
.
207. а) 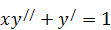 .
.
б) 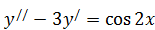 .
. 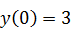 ,
, 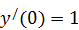 .
.
208. а) 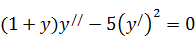 .
.
б) 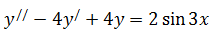 .
. 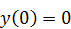 ,
, 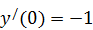 .
.
209. а) 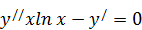 .
.
б) 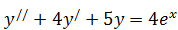 .
. 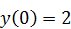 ,
, 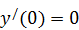 .
.
210. а) 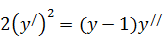 .
.
б) 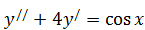 .
. 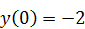 ,
, 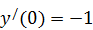 .
.
Задача 5.3
211. Найти закон движения материальной точки массы m, если известно, что работа силы, действующей в направлении движения, пропорциональна пути от начала этого движения (коэффициент пропорциональности k).
212. Лодка пущена со скоростью 4 км/ч через реку и прибыла на другой берег со скоростью 2 км/ч через 6 мин. Сила сопротивления воды пропорциональна квадрату скорости. Найти закон движения лодки и ширину реки.
213. У моторного судна при скорости 10 км/ч отключается мотор. Отрицательное ускорение, сообщаемое лодке сопротивлением воды, пропорционально скорости. Найти закон движения лодки.
214. Сила упругости, возникающая при растяжении пружины, пропорциональна увеличению ее длины и равна 1 Н, когда длина пружины увеличивается на 1 см. Найти закон движения груза, если его оттянуть книзу, а затем отпустить.
215. Кривая проходит через точку А(1; –2) и обладает тем свойством, что угловой коэффициент касательной в любой ее точке пропорционален квадрату ординаты точки касания с коэффициентом пропорциональности k = 2. Найти уравнение кривой.
216. Поезд, масса которого вместе с тепловозом равна М, движется прямолинейно. Сила тяги тепловоза постоянна и равна F. Сила f сопротивления движению поезда пропорциональна скорости движения. Найти закон движения поезда, если при t = 0, U = 0.
217. Локомотив весом р движется по некоторому участку пути со скоростью 60 км/ч. Через какой промежуток времени и на каком расстоянии от начала торможения он будет остановлен, если сила сопротивления движению при торможении равна 0,2 веса локомотива.
218. Вагоновожатый трамвая, включая реостат, постепенно увеличивает мощность двигателя так, что сила тяги возрастает от нуля пропорционально времени, увеличиваясь на 120 Н в секунду. Найти закон движения трамвая при следующих данных: 1) масса вагона М = 10 т; 2) сопротивление трению постоянно и равно 200 Н; 3) начальная скорость равна нулю.
219. Материальная точка массой m = 2 г погружается в жидкость, сила сопротивления которой пропорциональна скорости погружения с коэффициентом пропорциональности k = 0,002 кг/с. Найти скорость точки через 1 с после начала погружения, если в начальный момент она была равна нулю.
220. Скорость химической реакции, при которой разлагается данное вещество, пропорциональна количеству неразложившегося вещества. Через час после начала реакции осталось 36 г неразложившегося вещества, а через 3 час – 9 г. Сколько вещества было взято первоначально?
Задача5.4
Найти общее решение системы линейных дифференциальных уравнений. Сделать проверку найденного решения подстановкой в исходную систему уравнений. Решение проверить в MathCad.
| 221. | 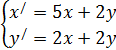 | 222. | 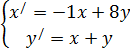 |
| 223. | 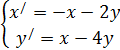 | 224. | 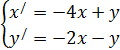 |
| 225. | 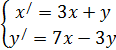 | 226. | 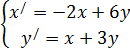 |
| 227. | 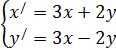 | 228. | 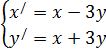 |
| 229. | 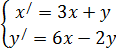 | 230. | 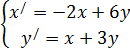 |
Задача 5.5
Выяснить, какие из данных рядов сходятся и какие расходятся. Решение проверить в MathCad.
| 231. | 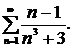 | 232. | 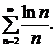 |
| 233. | 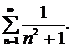 | 234. | 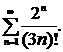 |
| 2 |
