Формула Муавра и эйлера. Извлечение корня из комплексного числа

Формула Эйлера названа в честь Леонарда Эйлера, который её ввёл, и связывает комплекснуюэкспоненту с тригонометрическими функциями.

Формула Эйлера утверждает, что для любого вещественного числа x выполнено следующее равенство:

,

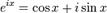где e — основание натурального логарифма,

i — мнимая единица.

Благодаря формуле Эйлера появилась так называемая тригонометрическая и показательная запись комплексного числа: .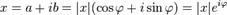

Также значительным следствием можно считать формулы возведения комплексного числа в произвольную степень: 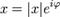, 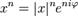. Геометрический смысл данной формулы следующий: при возведении числа x в степень n его расстояние до центра возводится в степень n, а угол поворота относительно оси OX увеличивается в n раз.

Формула возведения в степень верна не только для целых n, но и для вещественных. В частности, комплексная запись числа позволяет находить корни любой степени из любого комплексного числа, что и используется при доказательстве основной теоремы алгебры: «Многочлен степени n имеет ровно n комплексных корней»

Формула Муавра для комплексных чисел 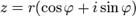, заданная в тригонометрической форме — формула

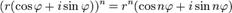для любого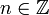

Формула Муавра сразу следует из формулы Эйлера 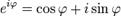и правила для экспонент 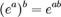, верного, если b — целое число. (Если b — не целое, то 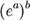— многозначная функция переменной a и 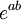— одно из её значений.)

Открыта французским математиком Абрахамом де Муавром.

Аналогичная формула применима также и при вычислении корней n-ой степени из ненулевого комплексного числа:

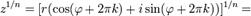
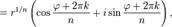
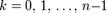
Отметим, что корни n-й степени из комплексного числа всегда существуют, и их количество равно n. На комплексной плоскости, как видно из формулы, все эти корни являются вершинами правильного n-угольника, вписанного в окружность радиуса 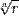с центром в точке 0.

Многочлены и их делимость.Теорема Безу.Основная теорема алгебры. Разложение многочлена на множители.Условие тождественности двух многочленов.Признак кратности корня многочлена и функции

Делимость многочлена

Многочлен, который можно представить в виде произведения многочленов низших степеней с коэффициентами из данного поля, называется приводимым (над данным полем), в противном случае — неприводимым. Неприводимые многочлены играют в кольце многочленов роль, сходную с ролью простых чисел в кольце целых чисел. Например, верна теорема: если произведение pq делится на неприводимый многочлен λ, то p или q делится на λ. Каждый многочлен, степени большей нуля, разлагается в данном поле в произведение неприводимых множителей единственным образом (с точностью до множителей нулевой степени).

Например, многочлен x⁴ − 2, неприводимый в поле рациональных чисел, разлагается на три множителя в поле вещественных чисел и на четыре множителя в поле комплексных чисел.

Вообще, каждый многочлен от одного переменного x разлагается в поле вещественных чисел на множители первой и второй степени, в поле комплексных чисел — на множители первой степени (основная теорема алгебры).

Для двух и большего числа переменных этого уже нельзя утверждать. Над любым полем для любого n > 2 существуют многочлен отn переменных, неприводимые в любом расширении этого поля. Такие многочлены называются абсолютно неприводимыми

Теорема Безу утверждает что остаток от деления многочлена P(x) на двучлен x − a равен P(a).

Предполагается, что коэффициенты многочлена содержатся в некотором коммутативномкольце с единицей (например, в полевещественных или комплексных чисел).

Основна́я теоре́ма а́лгебры утверждает, что

Всякий отличный от константы многочлен с комплексными коэффициентами имеет по крайней мере один корень вполе комплексных чисел.