Извлечение корня из комплексного числа

Корнем n-ой степени, n Î N, n ³ 2, из числа z называется любое комплексное число u, для которого n-ая степень равна z:

.

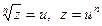В поле комплексных чисел справедлива следующая теорема.

Для любого z ≠ 0 извлечение корня n-ой степени, n ³ 2, из числа z всегда возможно и имеет ровно n различных значений.

Пусть z = r(cosj + isinj). Искомый корень n-ой степени обозначим

u = r(cosq + isinq).

По определению корня имеем uⁿ = z. Откуда следует, что

rⁿ (cosnq + isinnq) = r(cosj + isinj).

Из равенства комплексных чисел получаем:

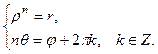
Так как .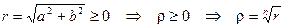

Таким образом, модуль комплексного числа u определяется как арифметический корень из действительного положительного числа r, а аргумент находят по формуле

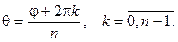
Общая формула Муавра

,

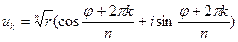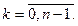
Пример.

Вычислить u = .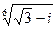

Представим число z = 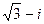в тригонометрической форме:

,

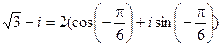Поэтому согласно общей формуле Муавра

,

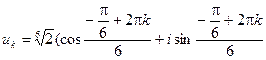где k = 0, 1, 2, 3, 4, 5.

Таким образом, значения корней:

,

,

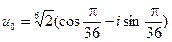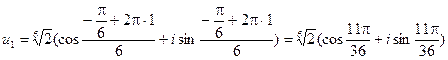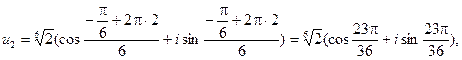
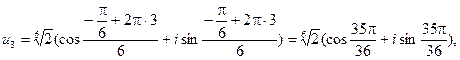
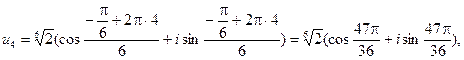
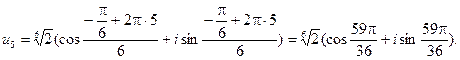
Геометрически корни можно интерпретировать как числа, изображающие в комплексной плоскости вершины правильного n угольника (в рассмотренном примере – шестиугольника ), вписанного в окружность радиусом 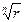(в рассмотренном примере – радиусом 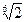), с центром в начале координат.

Примеры.

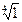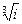Найти: 1) , 2) , 3) .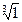

Решение.

1) ,

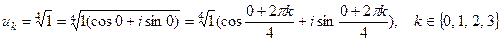u₀ = cos0 + isin0 = 1,

,

,

.

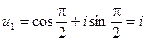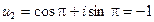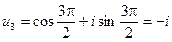2)

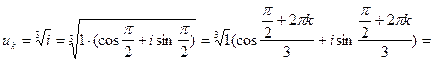
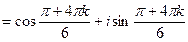, k = 0, 1, 2.

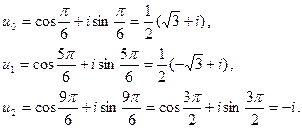
3) 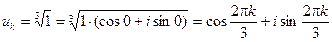, k = 0, 1, 2.

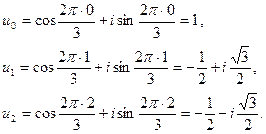
Формула Эйлера. Показательная форма комплексного числа

Помимо алгебраической и тригонометрической имеется еще показательная форма записи комплексного числа, которая широко используется в различных приложениях, в частности в электротехнике.

Пусть 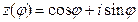, зависит от действительной переменной φ.

Сопоставим взаимно однозначным образом каждому комплексному числу 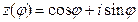комплексно показательное выражение 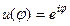. С помощью операций дифференцирования можно показать, что эти выражения имеют одну и ту же логическую сущность, в связи с этим полагают по определению

.

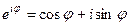Эта формула называется формулой Эйлера и представляет собой определение комплексной показательной функции 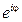, где φ – любое действительное число.

Пусть дано комплексное число z =r (cosφ + isinφ). Сопоставляя это с предыдущей формулой, получаем

.

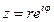Такая форма записи комплексного числа называется показательной формой комплексного числа.

В этой форме записи удобно осуществлять операции умножения, деления, возведения в степень и извлечения корня. Соответствующие формулы записываются следующим образом.

Пусть 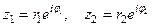. Тогда

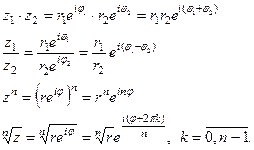
Примеры.

1. Найти показательную форму чисел:

а) z₁ = 1 + i; б) z₂ = .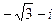

Решение.

а) r = , .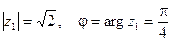

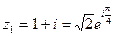б) .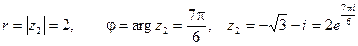

2. Найти алгебраическую форму чисел:

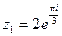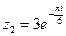а) , б) , в) .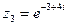

Решение.

а) ,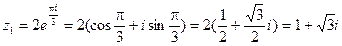

б) ,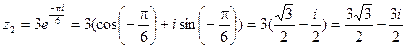

в) .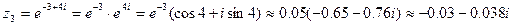

3. Найти z₁z₂ и 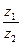, результат записать в тригонометрической форме:

а) 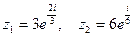; б) .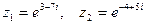

Решение.

а) ,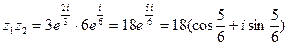

,

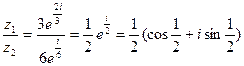б)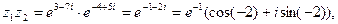

.

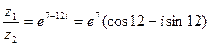4. Вычислить: а) z⁴ , б) 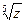, где .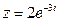

Решение:

а) ,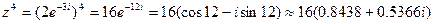

б)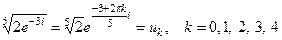

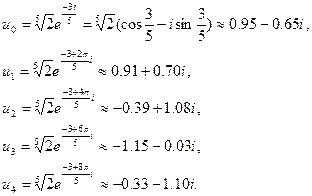
Теория комплексных чисел может быть использована при решении геометрических задач на плоскости; и обратно, факты геометрического характера позволяют доказывать некоторые соотношения и тождества для комплексных чисел.

Примеры.

1. Пусть 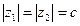. Доказать, что .

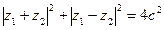Поскольку 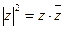, то

.

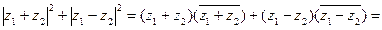
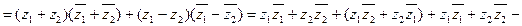
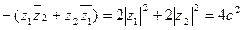Геометрически этот факт означает, что сумма квадратов длин диагоналей ромба равна сумме квадратов длин всех его сторон.

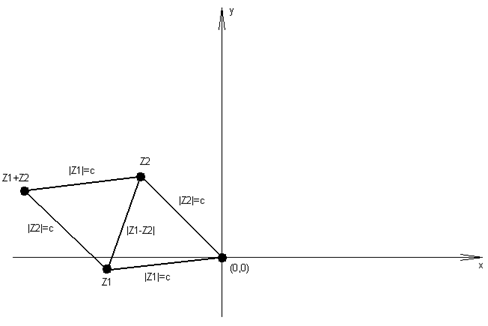Действительно, точки плоскости, соответствующие комплексным числам 0, z₁, z₂ и z₁ + z₂, являются вершинами ромба, для которого 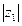и 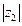– длины его сторон, а 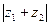и 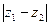– длины его диагоналей.

2. Пусть z₁, z₂, z₃, z₄ – различные комплексные числа и 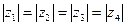. Доказать, что .

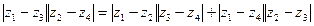Имеем:

=

= ,

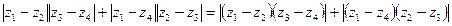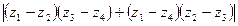т. к. число 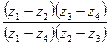вещественно и положительно (докажите это самостоятельно). Кроме того,

= = .

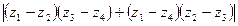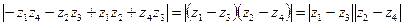Доказанное равенство известно в планиметрии как теорема Птолемея: произведение длин диагоналей выпуклого вписанного в окружность четырехугольника равно сумме парных произведений длин его противолежащих сторон.