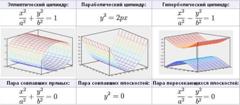
Смешанное произведение векторов и его свойства.

Смешанным произведением векторов наз. векторно-скалярное произведение, являющееся числом: a*b*c=[a*b]*c=a*[b*c], где

a={a_x,a_y,a_z}

b={b_x,b_y,b_z}

c={c_x,c_y,c_z}

Св-ва:
1. При перестановке 2х сомножителей:

a*b*c=-b*c*a

2. не меняется при перестановке циклических сомножителей:

a*b*c=c*a*b=b*c*a

3.а)(Геометрич. смысл) необходимым и достаточным условием компланарности 3х векторов явл. равенство a*b*c=0

б)если некомпланарные вектора a,b,c привести к 1 началу, то |a*b*c|=Vпараллепипеда, построенного на этих векторах

если a*b*c>0, то тройка a,b,c - правая

если a*b*c<0, то тройка a,b,c - левая

10.Прямая на плоскости и ее способы задания

Уравнение линии и поверхности.

1. Уравнение сферы. Сфера- геометрическое место точек, равноудаленных от 1ой точки, называемой центром.

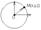O(a,b,c)

|OM|=r, OM={x-a,y-b,z-c}

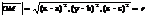
r²=(x-a)²+(y-b)²+(z-c)²- уравнение сферы. x²+y²+z²=r²- ур-е сферы с центром точке(0,0).

F(x,y,z)=0- ур-е поверхности - ур-ю, удовлетворяющему координатам x,y,z любой точки, лежащей на поверхности.

2. Уравнение окружности

|OM|=r, OM={x-a,y-b)

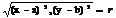
r²=(x-a)²+(y-b)²+(z-c)²- ур-е окружности

а=b=0, то x²+y²=r²

F(x,y)=0- ур-е линии на плоскости

Плоскость в пространстве

Плоскость в пространстве.

Ур-е в плоскости, проходящей через данную точку, перпендикулярно заданному вектору.

N-вектор нормали

M₀M{x-x₀,y-y₀,z-z₀}

Для того, чтобы точка MÎP, необходимо и достаточно чтобы вектора N^M₀M(т.е. N*M₀M=0)

A(x-x₀)+B(y-y₀)+С(z-z₀)=0 - ур-е плоскости, проходящей через данную точку ^вектору.

Прямая в пространстве

Векторное параметрическое уравнение прямой в пространстве:

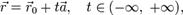
где 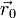— радиус-вектор некоторой фиксированной точки M₀, лежащей на прямой, 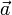— ненулевой вектор, коллинеарный этой прямой, 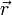— радиус-вектор произвольной точки прямой.

Параметрическое уравнение прямой в пространстве:

X0=ta y0=tb z0=tg

где 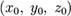— координаты некоторой фиксированной точки M₀, лежащей на прямой; 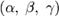— координаты вектора,коллинеарного

этой прямой.

Каноническое уравнение прямой в пространстве:

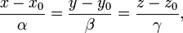
где 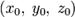— координаты некоторой фиксированной точки M₀, лежащей на прямой; 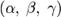— координаты вектора,коллинеарного этой прямой.

Общее векторное уравнение прямой в пространстве:

Поскольку прямая является пересечением двух различных непараллельных плоскостей, заданных соответственно общими уравнениям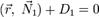и:

и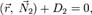

то уравнение прямой можно задать системой этих уравнений:

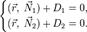
Кривые второго порядка

Кривая второго порядка — геометрическое место точек, декартовы прямоугольные координаты которых удовлетворяют уравнению вида

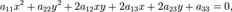
в котором по крайней мере один из коэффициентов 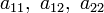отличен от нуля.

Общее уравнение в матричном виде

Общее уравнение кривой можно записать в матричном виде

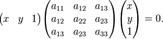
[править]Канонический вид

Вводом новой системы координат можно привести уравнения кривых второго порядка к стандартному каноническому виду (см. таблицу). Параметры канонических уравнений весьма просто выражаются через инварианты 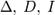и корни характеристического уравнения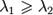

Невырожденные кривые

Кривая второго порядка называется невырожденной, если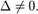

Кривая второго порядка называется вырожденной, если Δ = 0

Поверхность второго порядка

Поверхность второго порядка — геометрическое место точек, декартовы прямоугольные координаты которых удовлетворяют уравнению вида

a₁₁x² + a₂₂y² + a₃₃z² + 2a₁₂xy + 2a₂₃yz + 2a₁₃xz + 2a₁₄x + 2a₂₄y + 2a₃₄z + a₄₄ = 0

в котором по крайней мере один из коэффициентов a₁₁, a₂₂, a₃₃, a₁₂, a₂₃, a₁₃ отличен от нуля.