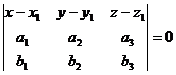Смешанное произведение векторов
Определение. Смешанным произведением векторов 
, 
и 
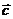называется число, равное скалярному произведению вектора на вектор, равный векторному произведению векторов и .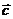
Обозначается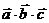 
или ( , , ).
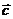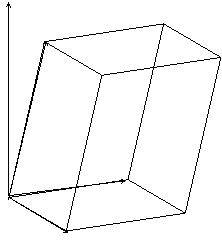
Смешанное произведение 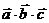по модулю равно объему параллелепипеда, построенного на векторах , и .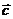
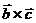
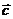
Свойства смешанного произведения:
1)Смешанное произведение равно нулю, если:
а) хоть один из векторов равен нулю;
б) два из векторов коллинеарны;
в) векторы компланарны.
2) 
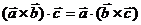
3) 
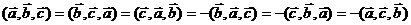
4) 
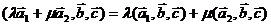
5) Объем треугольной пирамиды, образованной векторами , и 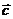, равен
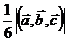
6)Если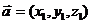 
, 
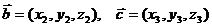, то
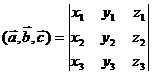
Пример. Доказать, что точки А(5; 7; 2), B(3; 1; -1), C(9; 4; -4), D(1; 5; 0) лежат в одной плоскости.
Найдем координаты векторов: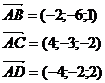 
Найдем смешанное произведение полученных векторов:
,
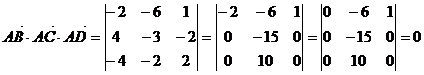Таким образом, полученные выше векторы компланарны, следовательно точки A, B, C и D лежат в одной плоскости.
Пример. Найти объем пирамиды и длину высоты, опущенной на грань BCD, если вершины имеют координаты A(0; 0; 1), B(2; 3; 5), C(6; 2; 3), D(3; 7; 2).
Найдем координаты векторов: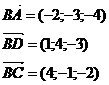 
Объем пирамиды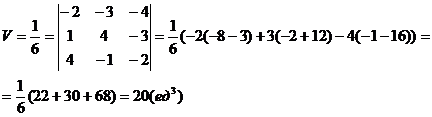 
Для нахождения длины высоты пирамиды найдем сначала площадь основания BCD.
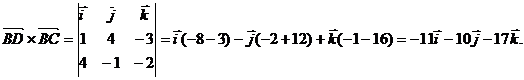
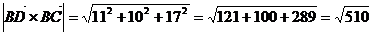
Sосн =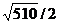 
(ед2)
Т.к. V =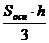 
; 
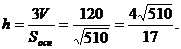(ед)
Уравнение поверхности в пространстве
Определение. Любое уравнение, связывающее координаты x, y, z любой точки поверхности является уравнением этой поверхности.
Общее уравнение плоскости
Определение. Плоскостьюназывается поверхность, все точки которой удовлетворяют общему уравнению:
Ax + By + Cz + D = 0,
где А, В, С – координаты вектора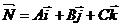 
-вектор нормали к плоскости.
Возможны следующие частные случаи:
А = 0 – плоскость параллельна оси Ох
В = 0 – плоскость параллельна оси Оу
С = 0 – плоскость параллельна оси Оz
D = 0 – плоскость проходит через начало координат
А = В = 0 – плоскость параллельна плоскости хОу
А = С = 0 – плоскость параллельна плоскости хОz
В = С = 0 – плоскость параллельна плоскости yOz
А = D = 0 – плоскость проходит через ось Ох
В = D = 0 – плоскость проходит через ось Оу
С = D = 0 – плоскость проходит через ось Oz
А = В = D = 0 – плоскость совпадает с плоскостью хОу
А = С = D = 0 – плоскость совпадает с плоскостью xOz
В = С = D = 0 – плоскость совпадает с плоскостью yOz
Уравнение плоскости, проходящей через три точки
Для того, чтобы через три какие- либо точки пространства можно было провести единственную плоскость, необходимо, чтобы эти точки не лежали на одной прямой.
Рассмотрим точки М1(x1, y1, z1), M2(x2, y2, z2), M3(x3, y3, z3) в общей декартовой системе координат.
Для того, чтобы произвольная точка М(x, y, z) лежала в одной плоскости с точками М1, М2, М3 необходимо, чтобы векторы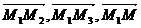 
были компланарны.
( 
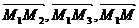) = 0
Таким образом,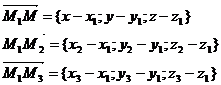 
Уравнение плоскости, проходящей через три точки:
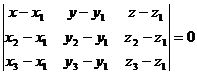
Уравнение плоскости по двум точкам и вектору, коллинеарному плоскости
Пусть заданы точки М1(x1, y1, z1), M2(x2, y2, z2) и вектор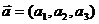 
.
Составим уравнение плоскости, проходящей через данные точки М1 и М2 и произвольную точку М(х, у, z) параллельно вектору .
Векторы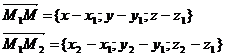 
и вектор 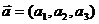должны быть компланарны, т.е.
( 
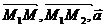) = 0
Уравнение плоскости:
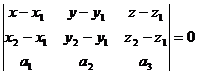
Уравнение плоскости по одной точке и двум векторам
Коллинеарным плоскости
Пусть заданы два вектора 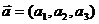и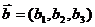 
, коллинеарные плоскости. Тогда для произвольной точки М(х, у, z), принадлежащей плоскости, векторы 
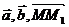должны быть компланарны.
Уравнение плоскости:
