Смешанное произведение векторов
Определение 9.3. Пусть даны три вектора  ,
,  и
и  . Умножим вектор
. Умножим вектор  на
на  векторно, а затем, векторное произведение
векторно, а затем, векторное произведение  ×
×  умножим скалярно на
умножим скалярно на  . В результате получим число (
. В результате получим число ( ×
×  )×
)×  , которое называют смешанным произведениетрёх векторов
, которое называют смешанным произведениетрёх векторов  ,
,  и
и  .
.
Теорема 9.3.Смешанное произведение ( ×
×  ) ×
) ×  трёх некомпланарных векторов равно объёму параллелепипеда, построенного на векторах
трёх некомпланарных векторов равно объёму параллелепипеда, построенного на векторах  ,
,  и
и  , связанному со знаком «+», если тройка
, связанному со знаком «+», если тройка  ,
,  ,
,  правая, и со знаком «−», если эта тройка – левая.
правая, и со знаком «−», если эта тройка – левая.
Доказательство. Рассмотрим параллелепипед, построенный на векторах  ,
,  и
и  (рисунок 9.5).
(рисунок 9.5).
 Построим вектор
Построим вектор  ×
×  и пусть
и пусть 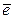 – единичный вектор, одинаково направленный с вектором
– единичный вектор, одинаково направленный с вектором  ×
× 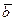 . Так как │
. Так как │ ×
× 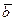 │= S – площадь параллелограмма OBDA, построенного на векторах
│= S – площадь параллелограмма OBDA, построенного на векторах  и
и 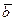 , то
, то  ×
× 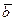 =
= 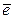 × S.
× S.
|
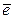 . Тогда по свойствам проекции векторов пре
. Тогда по свойствам проекции векторов пре  =
= 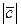 соsφ, где φ – угол между
соsφ, где φ – угол между  и осью ℓ. Тогда │пре
и осью ℓ. Тогда │пре  │= h, где h – высота параллелепипеда. Отметим, что если тройка
│= h, где h – высота параллелепипеда. Отметим, что если тройка  ,
,  ,
,  правая (рисунок 9.5), то h = пре
правая (рисунок 9.5), то h = пре  =
= 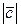 соsφ. Если же тройка
соsφ. Если же тройка  ,
, 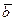 ,
,  левая, то h = − пре
левая, то h = − пре  = −
= − 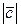 соsφ.
соsφ. Теперь,
( ×
× 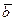 ) ×
) ×  =(
=( 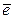 S) ×
S) ×  = (
= ( 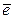 ×
×  )S =
)S = 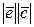 cosφ × S = S ×
cosφ × S = S × 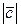 соsφ = ± S × h = ± Vпараллелепипеда,
соsφ = ± S × h = ± Vпараллелепипеда,
причём знак «+» берётся, если  ,
, 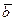 ,
,  – правая тройка, и знак «−», если она левая.
– правая тройка, и знак «−», если она левая.
 Следствие 9.5.Векторы
Следствие 9.5.Векторы  ,
, 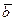 и
и  компланарны тогда и только тогда, когда их смешанное произведение (
компланарны тогда и только тогда, когда их смешанное произведение ( ×
× 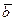 ) ×
) ×  = 0.
= 0.
Доказательство.
|
Отметим, что если тройка  ,
,  ,
,  правая, то тройка
правая, то тройка  ,
,  ,
,  также правая (рисунок 9.6, а), а если тройка
также правая (рисунок 9.6, а), а если тройка  ,
,  ,
,  левая, то тройка
левая, то тройка  ,
,  ,
,  также левая (рисунок 9.6, б).
также левая (рисунок 9.6, б).
Очевидно, что параллелепипед, построенный на векторах  ,
,  ,
,  и векторах
и векторах  ,
,  ,
,  – один и тот же. Поэтому
– один и тот же. Поэтому
( ×
×  ) ×
) ×  = ±Vпарал., (
= ±Vпарал., (  ×
×  ) ×
) ×  = ± Vпаралл..
= ± Vпаралл..
Так как тройки  ,
,  ,
,  и
и  ,
,  ,
,  либо обе правые, либо обе левые, то знак перед V выбирается в обоих произведениях одинаково. Поэтому
либо обе правые, либо обе левые, то знак перед V выбирается в обоих произведениях одинаково. Поэтому
( ×
× 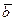 ) ×
) ×  = (
= ( 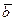 ×
×  ) ×
) ×  =
=  × (
× ( 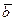 ×
×  ).
).
Ввиду следствия 9.5 смешанное произведение векторов  ,
, 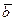 ,
,  ещё обозначают
ещё обозначают 
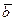
 .
.
Теорема 9.4.Если  = (х1; у1; z1),
= (х1; у1; z1),  = (х2; у2; z2),
= (х2; у2; z2),  = (х3; у3; z3),
= (х3; у3; z3),

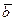
 =
= 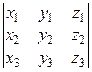 .
.
Доказательство.

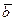
 = (
= ( ×
× 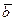 ) ×
) ×  = х3 ×
= х3 × 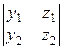 − у3 ×
− у3 × 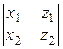 + z3 ×
+ z3 × 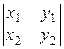 =
= 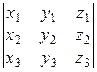 .
.
Пример.Найти объём параллелепипеда, построенного на векторах  = (3; 1; 2),
= (3; 1; 2), 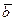 = (2; 2; 3),
= (2; 2; 3),  = (1; 3; 1).
= (1; 3; 1).
Решение.
V = │ 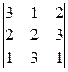 │= │6 + 12 + 3 – 4 – 27 – 2│= │−12│= 12 (куб. ед.).
│= │6 + 12 + 3 – 4 – 27 – 2│= │−12│= 12 (куб. ед.).
Ответ: 12.
Вопросы для самоконтроля
1. Что называют базисными векторами?
2. Что называется скалярным произведением двух векторов? Каковы его свойства?
3. Какие системы координат называют правыми (левыми)?
4. Что называется векторным произведением двух векторов? Каковы его свойства?
5. Что называется векторно-скалярным (смешанным) произведением векторов? Каковы его свойства?
Литература
1. Письменный, Д. Т. Конспект лекций по высшей математике : в 2 ч. / Д. Т. Письменный. – М. : Айрис-пресс, 2004. – 280 с.
2. Кремер, Н. Ш. Высшая математика для экономистов / Н. Ш. Кремер. – М. : «Юнити». 1997 г. – 439 с.
3. Минорский, В. П. Сборник задач по высшей математике / В. П. Минорский. – М., 1978. – 352 с.
4. Яблонский, А. И. Высшая математика /А. И. Яблонский. – Мн. : Высшая школа, 2000. – 351 с.
5. Гусак, А. А. Задачи и упражнения по высшей математике / А. А. Гусак. – Мн. : Высшая школа, 1988. – 544 с.
6. Гурский, Е. И. Руководство к решению задач по высшей математике / Е. И. Гурский. – Мн. : Высшая школа, 1989. – 348 с.
7. Александров, П. С. Курс аналитической геометрии и линейной алгебры / П. С. Александров. – М. : Наука, 1979. – 512 с.
8. Сборник задач по алгебре и аналитической геометрии / А. А. Бурдун [и др.]. – Мн. : Университетское, 1999. – 302 с.
9. Милованов, М. В. Алгебра и аналитическая геометрия / М. В. Милованов, Р. И. Тышкевич, А. С. Феденко. – Мн. : Вышэйшая школа, 1984. – 269 с.
10. Гусак, А. А. Аналитическая геометрия и линейная алгебра: справочное пособие по решению задач / А. А. Гусак. – Мн. : ТетраСистемс, 2001. – 288 с.
11. Тер-Крикоров, А. М. Курс математического анализа: учебное пособие для вузов / А. М. Тер-Крикоров, М. И. Шабунин. – М. : Наука Гл. ред. физ.-мат. Лит., 2001. – 672 с.
12. Пискунов, Н. С. Дифференциальное и интегральное исчисления для вузов / Н. С. Пискунов. – М.: Наука, 1970. – 560 с.
13. Бугров, Я. С. Высшая математика. Дифференциальные уравнения. Кратные интегралы. Ряды. Функция комплексного переменного / Я. С. Бугров, С. М. Никольский. – М. : Наука,1981. – 506 с.
14. Элементы линейной алгебры и аналитической геометрии / Р. Ф. Апатенок [и др.]. – Мн. : Вышэйшая школа, 1986. – 272 с.
15. Выготский, М. Я. Справочник по высшей математике / М. Я. Выготский. – М. : Наука, 1966. – 872 с.
16. Справочник по высшей математике / А. А. Гусак [и др.]. – Мн. : ТетраСистемс, 2000. – 638 с.
Производственно-практическое издание
БУЗЛАНОВ Александр Васильевич
БОРОДИЧЕлена Николаевна
БОРОДИЧ Руслан Викторович
БОРОДИЧ Тимур Викторович
Высшая математика:
