Координаты и векторы в пространстве. Применение векторов для нахождения углов между скрещивающимися прямыми и плоскостями Координаты точки на плоскости.
Координаты и векторы в пространстве. Применение векторов для нахождения углов между скрещивающимися прямыми и плоскостями Координаты точки на плоскости.
Рассмотрим в пространстве три взаимно перпендикулярные прямые. Их точка пересечения называется началом координат. Выбираем на прямых единичные отрезки и указываем положительное направление на прямых. Получаем три координатные прямые, называемые осями координат: ось ОХ (ось абсцисс), ось ОУ (ось ординат), ось OZ (ось аппликат).
Плоскости XOY,XOZ.YOZ – называются координатными плоскостями.
Проведем через точку М плоскости, перпендикулярные осям координат. Координаты точек пересечения этих плоскостей с осями координат называются координатами точки М в пространстве М(а,в,с).
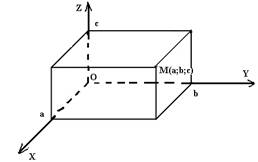
Нахождение длины отрезка и координат середины отрезка
Пусть А и В — произвольные точки плоскости с координатами А (х1; y1;z1) и В (х2; у2;z2) соответственно. Тогда длина отрезка :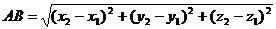 
Пусть М(х;у;z) середина отрезка АВ. Тогда верны формулы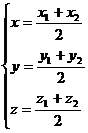 
Векторы и координаты
Величины, которые характеризуются не только численным значением, но и направлением, называют векторами. Геометрически векторы изображаются направленными отрезками. Вектор характеризуется следующими элементами: начальной точкой, направлением, длиной.
Если начало вектора есть А, а его конец В, то вектор обозначается символом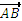 
Ненулевые векторы называются коллинеарными, если они, либо лежат на одной прямой, либо на параллельных прямых. Обозначаются коллинеарные векторы так: 
.
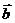Длина вектора – это длина отрезка, изображающего вектор.
Если два ненулевых вектора и 
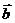коллинеарны и имеют одно направление – то они называются сонаправленными, если противоположное – то противоположно направленными.
Векторы называются равными, если они сонаправлены и их длины равны, т.е.
1) ↑↑
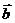
2) 
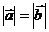
Сложение векторов
Если два вектора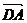 
и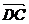 
выходят из одной точки, то их суммой будет вектор 
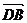совпадающий с диагональю параллелограмма, построенного на этих векторах , и выходящей из этой же точки(правило параллелограмма) + =
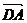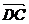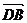
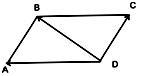
Если один вектор выходит из конца другого, то суммой будет вектор, соединяющий начало одного с концом другого (правило треугольника).
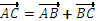
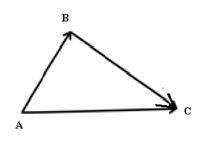
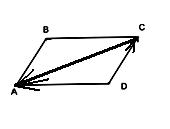
Если два вектора 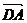и 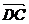выходят из одной точки, то разностью их будет вектор 
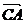совпадающий с диагональю параллелограмма, построенного на этих векторах, и выходящей из конца второго вектора в начало первого - = 
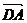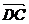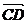
Произведением вектора на число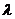 
называется вектор, обозначаемый 
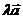, длина которого равна 
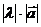и который сонаправлен с вектором , если 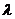>0 и противоположно направлен с ним, если 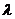<0.
ТЕОРЕМА Если точка М- середина отрезка АВ, то для любой точки Р верно равенство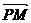 
= 
( 
+ 
)
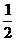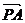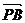ТЕОРЕМА. Два ненулевых вектора и 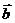коллинеарны тогда и только тогда, когда существует число 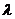, такое что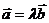 
Векторы называются компланарными, если они лежат в одной или в параллельных плоскостях.
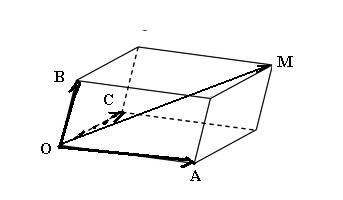
Для сложения трех некомпланарных векторов справедливо правило параллелепипеда: если три вектора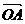 
, 
, 
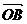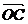отложены от одной точки и построен параллелепипед для которого отрезки OA,OB,OC- являются ребрами, то диагональ ОМ этого параллелепипеда изображает сумму векторов 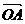, , 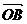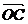.То есть + + = 
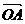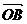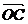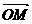
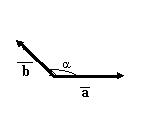
Угол между векторами
Углом между двумя векторами, отложенными от одной точки, называется кратчайший угол, на который нужно повернуть один из векторов вокруг своего начала до положения сонаправленности с другим вектором.
Координаты вектора
Если точка А имеет координаты (х1; у1;z1), а точка В имеет координаты (х2; у2;z2),
то координаты вектора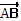 
это числа (x2-x1); (y2-y1); (z2-z1).
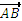
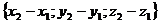, то есть чтобы найти координаты вектора надо из координат конца вектора вычесть соответственно координаты начала вектора.
В этом случае длина вектора выражается через его координаты следующим образом:
= 
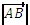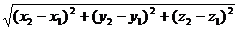
При сложении векторов складываются их координаты.
При умножении вектора на число k, на это число умножается каждая из его координат.
Если два вектора равны, то соответственно равны их координаты.
Задания с решением
- Найти координаты вектора
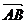и его длину, если A (2, 3 , -1) и B (1, -4, 5).
Решение
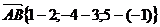, то есть 
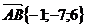.Тогда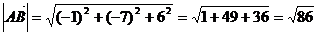 
Ответ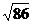 
2. Даны точки A (3, -2, 5), B (-4, 6, 1), C (-2, -6, -11), D (x, y, z). Найти x, y, z, если = .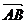
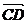Решение
Найдем координаты векторов 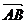и .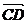
, 
.
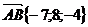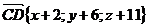Так как векторы равны, то равны и их соответствующие координаты, то есть имеем систему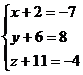 
Тогда 
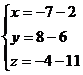или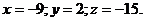 
Ответ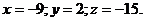
3.Даны координаты трёх вершин параллелограмма ABCD. A (3, -2, 1), B (-6, 4, 2), D (-3, 2,-4). Найдите координаты вершины С.
Решение
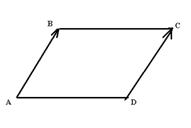
Так как ABCD – параллелограмм, то векторы 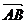и 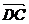равны..
Обозначим координаты точки С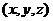 
Найдем координаты векторов 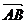и .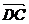
, 
.
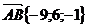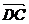
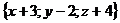Так как 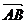= 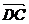, то равны и их соответствующие координаты, то есть имеем систему 
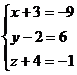Тогда 
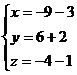или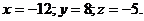 
Ответ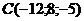 
4. Длина вектора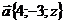 
равна 13. Найти z.
Решение
| |= 
= 
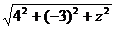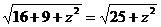.Получаем уравнение 
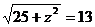.Возводим обе части уравнения в квадрат. Получаем 25+z2=169 или z2=169-25 z2=144. Откуда z=12 или z=-12
Ответ 12; -12
5. Даны векторы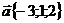 
и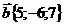 
. Найти координаты вектора 
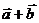и скалярные произведения векторов 
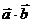и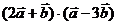 
Решение
При сложении векторов соответствующие координаты складываются, поэтому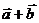 
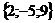
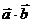=(-3)·5+1·(-6)+2·7=-15-6+14=23
Найдем координаты векторов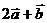 
и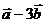 
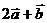
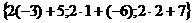, то есть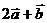 
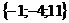
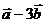
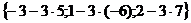, то есть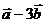 
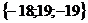
Тогда( 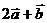)·( )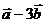=(-1)(-18)+(-4)19+11(-19)=18-76-209= -277
Ответ 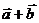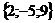; 23; -277
6. Точка Е середина ребра СС1 куба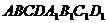 
. Найдите косинус угла между прямыми ВЕ и АD
Решение.
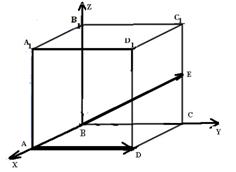
Будем использовать метод координат. Введем систему координат как показано на рисунке.
Рассмотрим векторы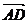 
и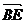 
.Пусть сторона куба равна а.
Тогда А(а;0;0), B(0;0;0), D(a;a;0), E(0:a;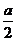 
)
Получаем: 
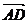
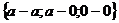и .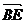 
,
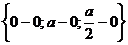то есть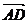 
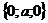и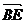 
.
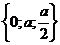Тогда по формуле для нахождения угла между векторами имеем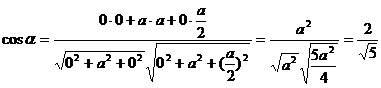 
Ответ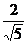 
7.В правильной четырехугольной призме 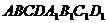со стороной основания 12 и высотой 21 на ребре 
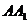взята точка М так, что 
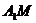=8. На ребре 
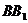взята точка K так, что 
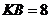. Найдите угол между плоскостью 
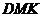и плоскостью 
.
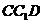Решение
. 
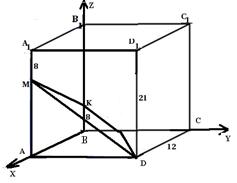
Так как мы будем использовать метод координат, сразу введем систему координат. Теперь перед нами стоит задача написать уравнения плоскости 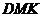и плоскости .
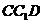Плоскость 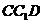это плоскость 
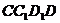.Она параллельна плоскости ХОZ и поэтому ее уравнение имеет вид у=12, так как призма правильная и сторона основания призмы равна 12.
Составим уравнение плоскости DMK.Найдем координаты точек D,M и K.
D (12;12;0), M(12;0;13), K(0;0;8).
Будем искать уравнение плоскости DMK в виде Ax + By + Cz + D = 0. Точки D,M и лежат на этой плоскости, поэтому имеем систему уравнений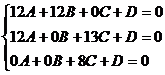 
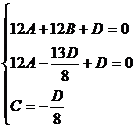
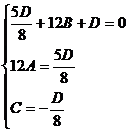
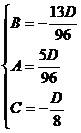
Подставим полученные выражения в уравнение плоскости .
Получим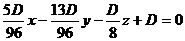 
.
Умножим обе части уравнения на 96 и разделим на D.
Получим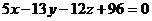 
. Это уравнение плоскости DMK.
Уравнение плоскости 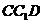у=12 или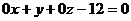 
Найдем косинус угла между плоскостями по формуле
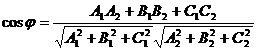
Получаем: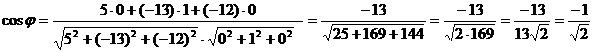 
Тогда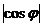 
= 
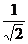и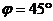 
Ответ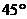 
Задания для самостоятельного решения
1. Точка М -середина отрезка АВ. Найти координаты точки М, если A (1, 3, -2), B (-5, 7, 3)
2.В треугольнике АВС: A (3, -1, -2), B (-5, 7, 4), C (1; 5; 2). Найти длину средней линии MN, где M и N - середины сторон AC и BC соответственно.
3. Найти длину СК - медианы треугольника АВС, где A (2, -4, 2), B (-10, -2,1 4), C (0; -3; 5).
4. Координаты точек: A (4; -3; 2), B (-1; -5; 4). Найти сумму координат точки С, лежащей на оси OY и равноудалённой от точек А и В.
6. Составить уравнение плоскости, проходящей через точки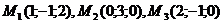 
7.Даны векторы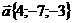 
и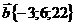 
. Найти 
.
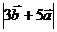8. Найти значения x, y, при которых векторы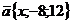 
и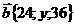 
коллинеарны.
9. Найти координаты вектора единичной длины, противонаправленного вектору .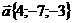
10. В кубе 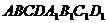найти вектор, равный сумме 
+ 
- 
.
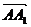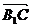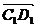11. 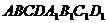' - куб.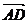 
, 
, 
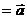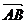
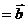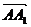
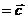. Выразить через векторы 
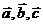вектор 
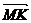,, если M - середина 
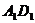' и K - середина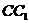 
12. Точка В делит отрезок АВ в отношении 2:3, считая от точки А. Найти координаты точки В, если А (1; -2; 4), В (6; 12; 9).
13. Векторы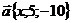 
и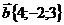 
перпендикулярны. Найти длину вектора .
14. Даны векторы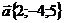 
и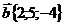 
. Найти угол между векторам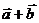и и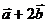 
.
15. Даны векторы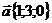 
и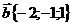 
. Найти вектор 
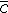, если он коллинеарен вектору 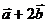, и его длина равна 
.
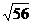16. Даны координаты точек C (3; -2; 1), D (-1; 2; 1), M (2; -3; 3), N(-1; 1, -2). Найти косинус угла между векторам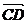и и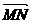 
.
17. Длина вектора равна 4, длина вектора 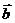равна 1, угол между векторами и 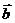равен 60º. Найти косинус угла между векторам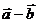и 
и .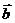
18. Найти длину вектора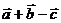 
, где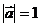 
, 
, 
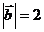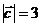. угол между векторами и 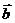равен 90º, угол между векторам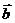и и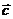 
равен 60º, угол между векторами и 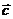равен 120º
19. Найти координаты вектора 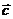, перпендикулярного векторам 
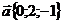и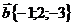 
и образующего тупой угол с осью OY, если 
.
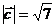20. В кубе 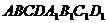' с ребром 1 найти · 
, · 
, · 
, · 
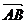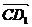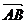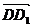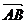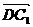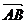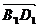
21.Даны точки А (9, 3, -5), В(2, -3, -5), С (2, -4,0 ), D( 6, -1, 3 )Найти координаты векторов 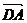и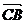 
Найти косинус угла между ними
22.Даны точки А(1.0,2),В(2,1,1),С(0,2.1)Найти косинус угла между векторам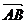и и -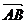 
.
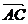23.Векторы {х,5,-10}и 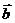в{4,-2,3 } перпендикулярны Найти длину вектора .
24. { 6, 0, -3} , { -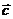 
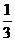, 0, -3}Найти координаты вектора + 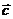и его длину
25.Даны точки А ( 3,5, -1) и В( 8,-4, -5) Найти координаты вектора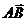 
26.Дана точка А ( 3,5, -1) и вектор 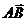{ 6, -5, -3}Найти координаты точки В
27. 
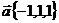
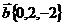
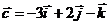Найти скалярное произведение 
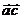Найти длину вектора
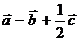
28. ABCDA'B'C'D' - правильная четырёхугольная призма. A (5; 0; 0), B (0; 0; 3), C (0; 5; 0).
1) найти координаты остальных вершин призмы,
2) найти координаты середины диагонали A'C,
3) найти координаты точки пересечения диагоналей грани BCC'B,
4) найти координаты точки пересечения медиан треугольника AB'C.
29.В прямоугольном параллелепипеде 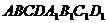известны ребра: 
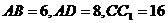, Найдите угол между плоскостями ABC и 
.
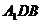30. .В кубе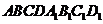 
точки E и F середины ребер 
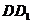и CD соответственно Найдите угол между прямыми 
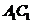и EF.
31.В кубе 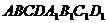найдите косинус угла между плоскостям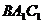и 
и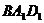 
.
32.В правильном тетраэдре ABCD найдите угол между высотой тетраэдра DH и медианой BM боковой грани BCD.
33.В правильной шестиугольной пирамиде SABCDEF стороны основания которой равны 1, а боковые ребра равны 2, найдите угол между прямыми SB и CD.
Координаты и векторы в пространстве. Применение векторов для нахождения углов между скрещивающимися прямыми и плоскостями Координаты точки на плоскости.
Рассмотрим в пространстве три взаимно перпендикулярные прямые. Их точка пересечения называется началом координат. Выбираем на прямых единичные отрезки и указываем положительное направление на прямых. Получаем три координатные прямые, называемые осями координат: ось ОХ (ось абсцисс), ось ОУ (ось ординат), ось OZ (ось аппликат).
Плоскости XOY,XOZ.YOZ – называются координатными плоскостями.
Проведем через точку М плоскости, перпендикулярные осям координат. Координаты точек пересечения этих плоскостей с осями координат называются координатами точки М в пространстве М(а,в,с).