Декартовы прямоугольные координаты в пространстве. Координаты точек. Координаты векторов. Деление отрезка в данном отношении
 Декартова прямоугольная система координат в пространстве определяется заданием единицы масштаба для измерения длин и трех пересекающихся в точке взаимно перпендикулярных осей, первая из которых называется осью абсцисс
Декартова прямоугольная система координат в пространстве определяется заданием единицы масштаба для измерения длин и трех пересекающихся в точке взаимно перпендикулярных осей, первая из которых называется осью абсцисс 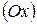 , вторая – осью ординат
, вторая – осью ординат 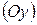 , третья – осью аппликат
, третья – осью аппликат 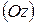 ; точка
; точка 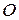 ‑ начало координат (Рис. 4.4).
‑ начало координат (Рис. 4.4).


Положение координатных осей можно задать с помощью единичных векторов 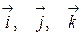 , направленных соответственно по осям
, направленных соответственно по осям 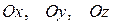 . Векторы
. Векторы 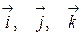 называются основными или базисными ортами и определяют базис
называются основными или базисными ортами и определяют базис 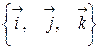 в трехмерном пространстве.
в трехмерном пространстве.
Пусть в пространстве дана точка 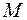 . Проектируя ее на ось
. Проектируя ее на ось 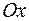 , получим точку
, получим точку 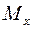 . Первой координатой
. Первой координатой 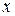 или абсциссой точки
или абсциссой точки 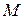 называется длина вектора
называется длина вектора 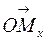 , взятая со знаком плюс, если
, взятая со знаком плюс, если 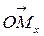 направлен в ту же сторону, что и вектор
направлен в ту же сторону, что и вектор 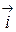 , и со знаком минус ‑ если в противоположную. Аналогично проектируя точку
, и со знаком минус ‑ если в противоположную. Аналогично проектируя точку 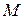 на оси
на оси 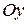 и
и 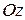 , определим ее ординату
, определим ее ординату 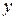 и аппликату
и аппликату 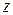 . Тройка чисел
. Тройка чисел 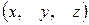 взаимно однозначно соответствует точке
взаимно однозначно соответствует точке 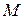 .
.
Система координат называется правой, если вращение от оси 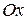 к оси
к оси 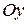 в ближайшую сторону видно с положительного направления оси
в ближайшую сторону видно с положительного направления оси 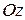 совершающимися против часовой стрелки, и левой, если вращение от оси
совершающимися против часовой стрелки, и левой, если вращение от оси 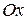 к оси
к оси 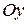 в ближайшую сторону видно совершающимися по часовой стрелке.
в ближайшую сторону видно совершающимися по часовой стрелке.
Вектор 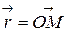 , направленный из начала координат в точку
, направленный из начала координат в точку 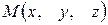 называется радиус-вектором точки
называется радиус-вектором точки 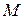 , т.е.:
, т.е.:
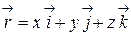 | (4.6) |
Если даны координаты точек 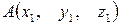 и
и 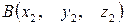 , то координаты вектора
, то координаты вектора 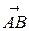 получаются вычитанием из координат его конца
получаются вычитанием из координат его конца 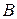 координат начала
координат начала  :
: 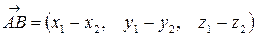 или
или 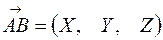 .
.
Следовательно, по формуле (4.5):
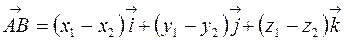 или или 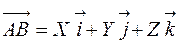 | (4.7) |
При сложении (вычитании) векторов их координаты складываются (вычитаются), при умножении вектора на число все его координаты умножаются на это число.
Длина вектора 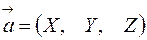 равна квадратному корню из суммы квадратов его координат.
равна квадратному корню из суммы квадратов его координат.
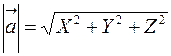 . . | (4.8) |
Длина вектора 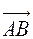 , заданного координатами своих концов, т.е. расстояние между точками
, заданного координатами своих концов, т.е. расстояние между точками  и
и 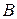 вычисляется по формуле:
вычисляется по формуле:
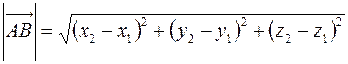 . . | (4.9) |
Если 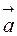 и
и 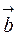 коллинеарны, то они отличаются друг от друга скалярным множителем. Следовательно, у коллинеарных векторов координаты пропорциональны:
коллинеарны, то они отличаются друг от друга скалярным множителем. Следовательно, у коллинеарных векторов координаты пропорциональны:
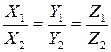 . . | (4.10) |
Пусть точка 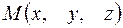 делит отрезок между точками
делит отрезок между точками 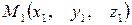 и
и 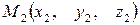 в отношении
в отношении 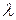 , тогда радиус-вектор точки
, тогда радиус-вектор точки 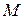 выражается через радиусы-векторы
выражается через радиусы-векторы 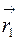 и
и 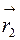 его концов по формуле:
его концов по формуле: 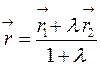 .
.
Отсюда получаются координатные формулы:
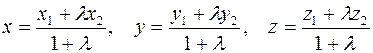 .
.
В частности, если точка 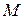 делит отрезок
делит отрезок 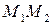 пополам, то
пополам, то 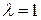 и
и 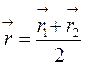 , т.е.
, т.е. 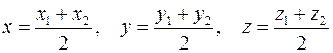 .
.
Направляющие косинусы
Пусть дан вектор 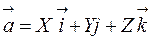 . Единичный вектор того же направления, что и
. Единичный вектор того же направления, что и 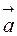 (орт вектора
(орт вектора 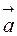 ) находится по формуле:
) находится по формуле:
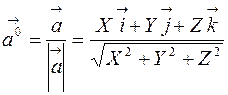 .
.
Пусть ось 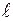 образует с осями координат углы
образует с осями координат углы 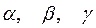 . Направляющими косинусами оси
. Направляющими косинусами оси 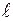 называются косинусы этих углов:
называются косинусы этих углов: 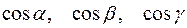 . Если направление
. Если направление 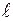 задано единичным вектором
задано единичным вектором 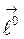 , то направляющие косинусы служат его координатами, т.е.:
, то направляющие косинусы служат его координатами, т.е.:
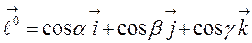 .
.
Направляющие косинусы связаны между собой соотношением:
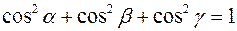 .
.
Если направление 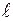 задано произвольным вектором
задано произвольным вектором 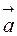 , то находят орт этого вектора и, сравнивая его с выражением для единичного вектора
, то находят орт этого вектора и, сравнивая его с выражением для единичного вектора 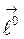 , получают:
, получают:
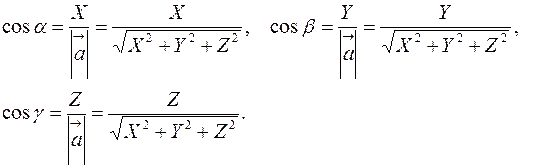
Скалярное произведение
Скалярными произведением 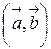 двух векторов
двух векторов 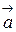 и
и 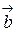 называется число, равное произведению их длин на косинус угла между ними:
называется число, равное произведению их длин на косинус угла между ними: 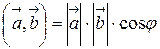 .
.
Скалярное произведение обладает следующими свойствами:
1. 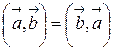 ;
;
2. 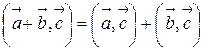 ;
;
3. 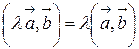 ;
;
4. Если 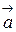 и
и 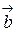 ‑ ненулевые векторы, то
‑ ненулевые векторы, то 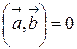 тогда и только тогда, когда эти векторы перпендикулярны. Если
тогда и только тогда, когда эти векторы перпендикулярны. Если 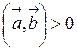 , то угол между
, то угол между 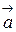 и
и 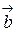 - острый, если
- острый, если 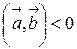 , то угол - тупой;
, то угол - тупой;
5. Скалярный квадрат вектора 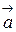 равен квадрату его длины, т.е.
равен квадрату его длины, т.е. 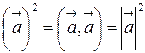 .
.
Следовательно, 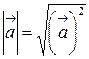 .
.
Геометрический смысл скалярного произведения: скалярное произведение вектора на единичный вектор 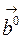 равно проекции вектора
равно проекции вектора 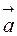 на направление, определяемое
на направление, определяемое 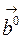 , т.е.
, т.е. 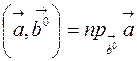 .
.
Из определения скалярного произведения вытекает следующая таблица умножения ортов 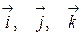 :
:
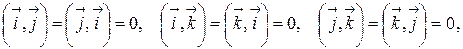
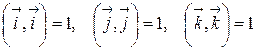 .
.
Если векторы заданы своими координатами 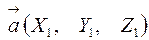 и
и 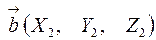 , т.е.
, т.е. 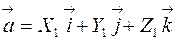 ,
, 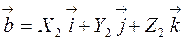 , то, перемножая эти векторы скалярно и используя таблицу умножения ортов, получим выражение скалярного произведения
, то, перемножая эти векторы скалярно и используя таблицу умножения ортов, получим выражение скалярного произведения 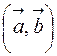 через координаты векторов:
через координаты векторов:
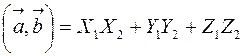 .
.
Векторное произведение
Векторным произведением вектора 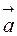 на вектор
на вектор 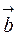 называется вектор
называется вектор 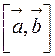 , длина и направление которого определяется условиями:
, длина и направление которого определяется условиями:
1. 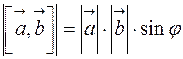 , где
, где 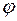 ‑ угол между
‑ угол между 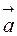 и
и 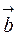 ;
;
2. 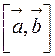 перпендикулярен каждому из векторов
перпендикулярен каждому из векторов 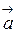 и
и 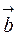 ;
;
3. 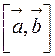 направлен так, что кратчайший поворот от
направлен так, что кратчайший поворот от 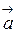 к
к 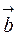 виден из его конца совершающимся против часовой стрелки.
виден из его конца совершающимся против часовой стрелки.
Векторное произведение обладает следующими свойствами:
1. 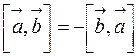 ;
;
2. 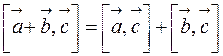 ;
;
3. 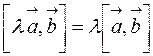 ;
;
4. Векторное произведение равно нулю (нуль вектору) тогда и только тогда, когда 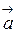 и
и 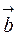 коллинеарны. В частности,
коллинеарны. В частности, 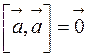 для любого вектора
для любого вектора 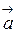 ;
;
5. Если 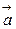 и
и 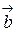 неколлинеарны, то модуль векторного произведения равен площади параллелограмма
неколлинеарны, то модуль векторного произведения равен площади параллелограмма 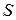 построенного на этих векторах, как на сторонах.
построенного на этих векторах, как на сторонах.
Из первых трех свойств следует, что векторное умножение суммы векторов на сумму векторов подчиняется обычным правилам перемножения многочленов. Надо только следить за тем, чтобы порядок следования множителей не менялся.
Основные орты перемножаются следующим образом:
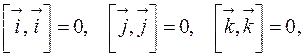
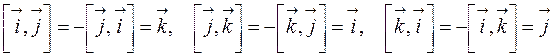 .
.
Если 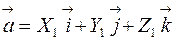 и
и 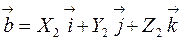 , то c учетом свойств векторного произведения векторов, можно вывести правило вычисления координат векторного произведения по координатам векторов-сомножителей:
, то c учетом свойств векторного произведения векторов, можно вывести правило вычисления координат векторного произведения по координатам векторов-сомножителей:
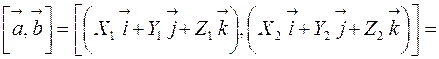
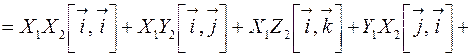
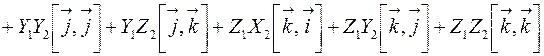 .
.
Если принять во внимание полученные выше правила перемножения ортов, то:
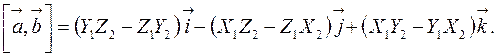 | (4.11) |
Более компактную форму записи выражения для вычисления координат векторного произведения двух векторов можно построить, если ввести понятие определителя матрицы.
Рассмотрим частный случай, когда вектора 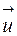 и
и 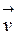 принадлежат плоскости
принадлежат плоскости 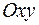 , т.е. их можно представить как
, т.е. их можно представить как 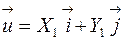 и
и 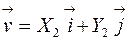 .
.
Если координаты векторов записать в виде таблицы следующим образом: 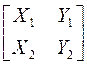 , то можно сказать, что из них сформирована квадратная матрица второго порядка, т.е. размером
, то можно сказать, что из них сформирована квадратная матрица второго порядка, т.е. размером 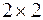 , состоящая из двух строк и двух столбцов. Каждой квадратной матрице ставится в соответствие число, которое вычисляется из элементов матрицы по определенным правилам и называется определителем. Определитель матрицы второго порядка равен разности произведений элементов главной диагонали и побочной диагонали:
, состоящая из двух строк и двух столбцов. Каждой квадратной матрице ставится в соответствие число, которое вычисляется из элементов матрицы по определенным правилам и называется определителем. Определитель матрицы второго порядка равен разности произведений элементов главной диагонали и побочной диагонали:
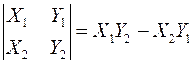 .
.
В таком случае:
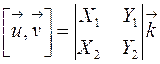
Абсолютная величина определителя, таким образом, равна площади параллелограмма, построенного на векторах 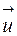 и
и 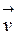 , как на сторонах.
, как на сторонах.
Если сравнить это выражение с формулой векторного произведения (4.7), то:
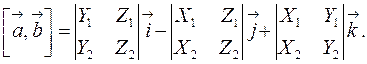 | (4.12) |
Это выражение представляет собой формулу для вычисления определителя матрицы третьего порядка по первой строке.
Таким образом:
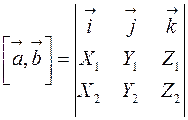
Определитель матрицы третьего порядка вычисляется следующим образом:
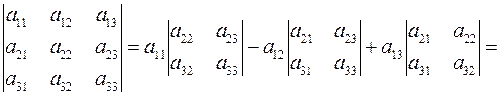
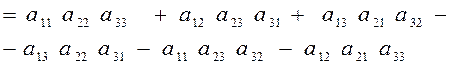
и представляет собой алгебраическую сумму шести слагаемых.
Формулу для вычисления определителя матрицы третьего порядка легко запомнить, если воспользоваться правилом Саррюса, которое формулируется следующим образом:
· Каждое слагаемое является произведением трех элементов, расположенных в разных столбцах и разных строках матрицы;
· Знак “плюс” имеют произведения элементов, образующих треугольники со стороной, параллельной главной диагонали;
· Знак “минус” имеют произведения элементов, принадлежащих побочной диагонали, и два произведения элементов, образующих треугольники со стороной, параллельной побочной диагонали.
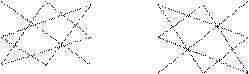
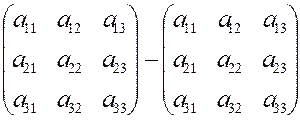
Смешанное произведение
Смешанным произведением тройки векторов 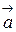 ,
, 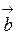 и
и 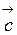 называется число, равное скалярному произведению вектора
называется число, равное скалярному произведению вектора 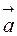 на векторное произведение
на векторное произведение 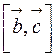 . Если рассматриваемые векторы
. Если рассматриваемые векторы 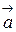 ,
, 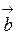 и
и 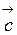 некомпланарны, то векторное произведение
некомпланарны, то векторное произведение 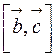 есть вектор, длина которого численно равна площади построенного на них параллелограмма. Направлен этот вектор по нормали к плоскости параллелограмма. Если этот вектор скалярно умножить на вектор
есть вектор, длина которого численно равна площади построенного на них параллелограмма. Направлен этот вектор по нормали к плоскости параллелограмма. Если этот вектор скалярно умножить на вектор 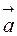 , то получившееся число будет равно произведению площади основания параллелепипеда, построенного на тройке векторов
, то получившееся число будет равно произведению площади основания параллелепипеда, построенного на тройке векторов 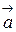 ,
, 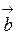 и
и 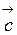 , и его высоты, т.е. объему этого параллелепипеда.
, и его высоты, т.е. объему этого параллелепипеда.
Таким образом, смешанное произведение векторов 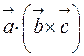 (которое обозначается
(которое обозначается 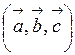 ) есть число, абсолютная величина которого выражает объем параллелепипеда, построенного на векторах
) есть число, абсолютная величина которого выражает объем параллелепипеда, построенного на векторах 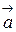 ,
, 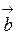 и
и 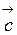 .
.
Знак произведение положителен, если векторы 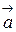 ,
, 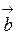 и
и 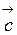 , образуют правую тройку векторов, т.е. вектор
, образуют правую тройку векторов, т.е. вектор 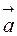 направлен так, что кратчайший поворот от
направлен так, что кратчайший поворот от 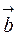 к
к 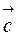 виден из его конца совершающимся против часовой стрелки.
виден из его конца совершающимся против часовой стрелки.
Из геометрического смысла смешанного произведения непосредственно следует необходимое и достаточное условие некомпланарности векторов 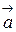 ,
, 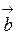 и
и 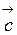 : для того, чтобы векторы
: для того, чтобы векторы 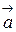 ,
, 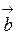 и
и 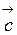 были некомпланарными необходимо и достаточно, чтобы их смешанное произведение было отлично от нуля.
были некомпланарными необходимо и достаточно, чтобы их смешанное произведение было отлично от нуля.
Если 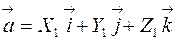
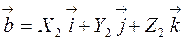 , и
, и 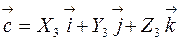 , то:
, то:
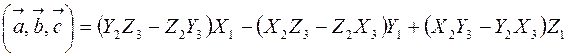 ,
,
или в свернутой форме:
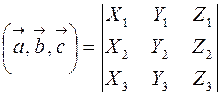 .
.
Справедливы следующие свойства смешанного произведения векторов:
1. Смешанное произведение не меняется при циклической перестановке его сомножителей 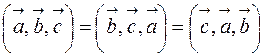 ;
;
2. При перестановке двух соседних множителей смешанное произведение меняет свой знак на противоположный 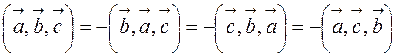 .
.
Контрольные вопросы к лекции №4
1. Понятие скалярной величины.
2. Понятие векторной величины.
3. Понятия единичного вектора и нулевого вектора.
4. Модуль вектора, формула расстояния между двумя точками.
5. Понятие коллинеарности векторов.
6. Понятие компланарности векторов.
7. Понятие проекции вектора на ось.
8. Линейные операции над векторами.
9. Скалярое произведение векторов.
10. Векторное произведение векторов.
11. Смешанное произведение векторов.
Лекция 5. Прямая
Основные понятия:
векторное параметрическое уравнение прямой; параметрические уравнения прямой в пространстве; канонические уравнения прямой; направляющий вектор прямой.
Основные понятия
Прямая 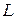 в пространстве может быть однозначно определена, если известна точка, принадлежащая прямой, и ненулевой вектор, параллельный прямой (направляющий вектор прямой).
в пространстве может быть однозначно определена, если известна точка, принадлежащая прямой, и ненулевой вектор, параллельный прямой (направляющий вектор прямой).
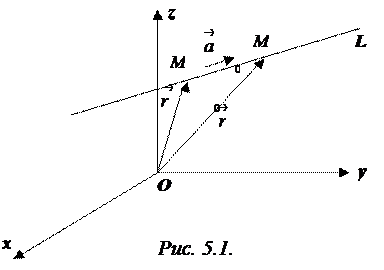 Пусть задана такая точка
Пусть задана такая точка 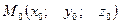 и вектор
и вектор 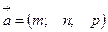 (Рис. 5.1).
(Рис. 5.1).
Если 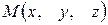 ‑ произвольная текущая точка прямой
‑ произвольная текущая точка прямой 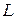 , то вектор
, то вектор 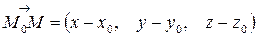 коллинеарен вектору
коллинеарен вектору 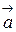 и их соответствующие координаты пропорциональны.
и их соответствующие координаты пропорциональны.
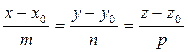 | (5.1) |
Этим соотношениям удовлетворяют координаты любой точки прямой 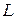 и только этой прямой. Равенства (5.1) называются каноническими уравнениями прямой в пространстве.
и только этой прямой. Равенства (5.1) называются каноническими уравнениями прямой в пространстве.
Обозначим 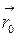 радиус-вектор точки
радиус-вектор точки 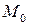 ,
, 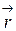 ‑ радиус-вектор точки
‑ радиус-вектор точки 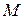 . Тогда:
. Тогда:
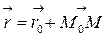 | (5.2) |
В силу коллинеарности векторов 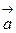 и
и 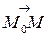 существует число
существует число 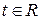 такое, что
такое, что 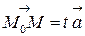 . Тогда из (5.2) получим векторное параметрическое уравнение прямой:
. Тогда из (5.2) получим векторное параметрическое уравнение прямой:
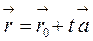 | (5.3) |
В координатной форме уравнение (5.3) равносильно трем уравнениям:
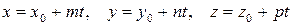 , , 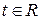 , , | (5.4) |
которые называются параметрическими уравнениями прямой в пространстве.
Исключая из уравнений (5.4) параметр 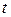 , легко перейти к каноническим уравнениям прямой (5.1).
, легко перейти к каноническим уравнениям прямой (5.1).
Обратный переход от (5.1) к (5.4) осуществляют, приравнивая каждое из трех соотношений (5.1) к 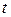 . При этом, если знаменатель какого-либо соотношения равен нулю, то необходимо приравнять к нулю его числитель.
. При этом, если знаменатель какого-либо соотношения равен нулю, то необходимо приравнять к нулю его числитель.
Пусть заданы точки 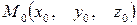 и
и 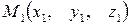 . Составим уравнение прямой, проходящей через заданные точки, пользуясь
. Составим уравнение прямой, проходящей через заданные точки, пользуясь
рис. 5.1.
Очевидно, что в этом случае направляющим вектором прямой 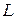 будет вектор
будет вектор 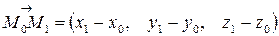 . Используя (5.1), получаем искомые уравнения в виде:
. Используя (5.1), получаем искомые уравнения в виде:
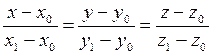 | (5.5) |
Прямую 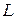 в пространстве можно определить как пересечение двух плоскостей. Рассматривая совместно уравнения этих плоскостей, получим уравнение линии
в пространстве можно определить как пересечение двух плоскостей. Рассматривая совместно уравнения этих плоскостей, получим уравнение линии 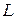 в общем виде:
в общем виде:
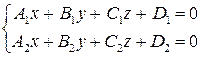 | (5.6) |
Система двух уравнений первой степени (5.6) определяет прямую линию при условии, что нормальные векторы 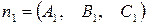 и
и 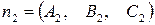 неколлинеарны. Только в этом случае плоскости будут пересекаться. Уравнения (5.6) носят название «общее уравнение прямой в пространстве».
неколлинеарны. Только в этом случае плоскости будут пересекаться. Уравнения (5.6) носят название «общее уравнение прямой в пространстве».
Чтобы перейти от общих уравнений прямой (5.6) к ее каноническим уравнениям (5.1), нужно на прямой найти какую-нибудь точку 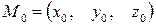 и определить ее направляющий вектор
и определить ее направляющий вектор 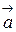 .
.
Точку 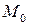 находят, давая произвольное значение одной из переменных
находят, давая произвольное значение одной из переменных 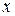 ,
, 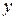 или
или 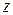 . Решая систему (5.6), получают значения оставшихся двух переменных.
. Решая систему (5.6), получают значения оставшихся двух переменных.
Направляющий вектор 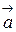 параллелен линии пересечения плоскостей (5.6) и, следовательно, перпендикулярен обоим нормальным векторам плоскостей:
параллелен линии пересечения плоскостей (5.6) и, следовательно, перпендикулярен обоим нормальным векторам плоскостей:
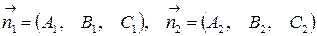 .
.
Поэтому в качестве 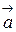 можно взять вектор:
можно взять вектор:
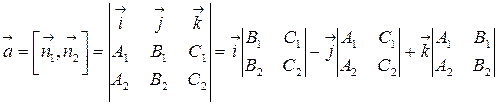
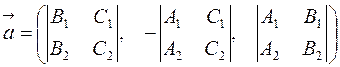 | (5.7) |
