Свойства операции транспонирования матриц

1) (А + В)^Т = А^Т + В^Т;

2) (АВ)^Т = В^Т А^Т;

3) (kА)^Т = kА^Т;

4) (А^–1)^Т = (А^Т)^–1,

где k– число, А иВ – матрицы.

МатрицаАназывается симметрической, если А = А^Т.

Ортогональной называется матрицаА, для которой А^Т = А^–1.

Следующие три условия равносильны:

1) матрицаА ортогональна;

2) матрицаА^–1 ортогональна;

3) столбцы матрицыА образуют ортонормированную систему векторов.

Ортогональная матрица может не иметь действительных собственных значений.

Симметрическая матрица всегда имеет действительные собственные значения, и все ее собственные значения – действительные числа. Собственные векторы симметрической матрицы, принадлежащие различным собственным значениям, ортогональны.

Для каждой симметрической матрицыА существует такая ортогональная матрица Q, что

Q^–1А Q– диагональная матрица. Построение этой ортогональной матрицы осуществляется следующим образом:

1) строим невырожденную матрицуТ, которая приводит матрицу А к диагональному виду;

2) подвергаем столбцы найденной матрицыТ процессу ортогонализации Шмидта, а затем нормируем полученные векторы;

3) строим ортогональную матрицу Q, столбцами которой являются координаты полученной в п.2 ортонормированной системы векторов.

Пример.Привести к диагональному виду с помощью ортогональной матрицы симметрическую матрицуА = .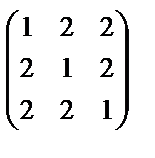

Р е ш е н и е. Характеристическое уравнение матрицы Аимеет вид:

| A – λE |= 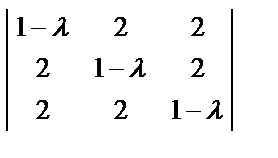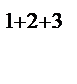= = 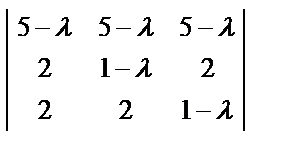(5 –λ)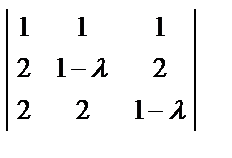 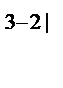= (5 – λ) 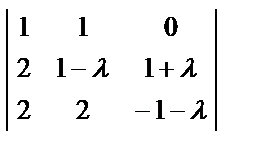= (5 – λ) (1 + λ)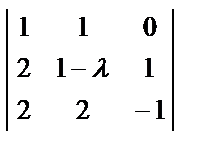 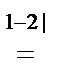(5 – λ) (1 + λ) 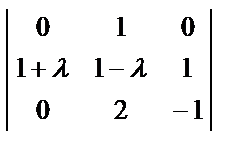=(5 – λ) (1 + λ)² = 0.

Отсюда следует, что матрицаА имеет два собственных значения: λ₁ = –1, λ₂ = 5.

Фундаментальная система решений системы уравнений (A + E) х = θ состоит из двух векторов

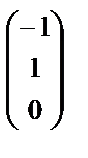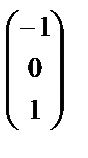и , а система уравнений(A – 5E) х = θ– из одного вектора 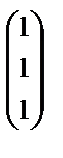(вычисления провести самостоятельно).

МатрицаТ, приводящая матрицу А к диагональному виду, имеет вид Т = .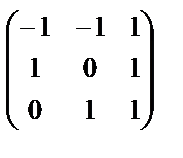

После ортогонализации и нормирования столбцов этой матрицы получим ортогональную матрицу

Q= .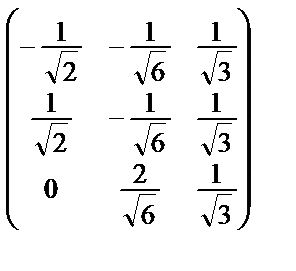

Матрица, обратная к Q, совпадает с Q^Т, т.е., Q^–1 = .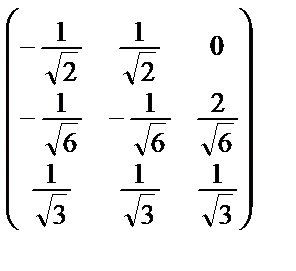

Нетрудно проверить, что Q^–1А Q = .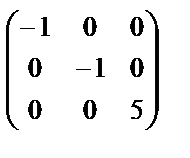

Задания.Привести к диагональному виду с помощью ортогональной матрицы следующие матрицы:

1. А = 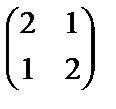, 2. А₂ = 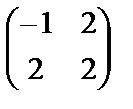, 3. А₃ = 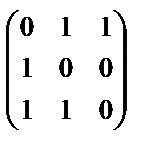, 4. А₄ = .

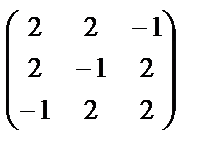2.4.Квадратичные формы

Переход от системы n неизвестных х₁, х₂, … , х_n к системе n неизвестных

у₁, у₂, … , у_n по формуле x = Sy, где х = х(х₁, х₂, … , х_n), у = у(у₁, у₂, … , у_n), S– квадратная матрица порядка n, называется линейным преобразованием неизвестных. Если S– невырожденная матрица, то линейное преобразование неизвестных также называется невырожденным.

Квадратичной формойF(х₁, х₂, … , х_n) от n неизвестных х₁, х₂, … , х_n называется сумма, каждое слагаемое которой является или квадратом одного из этих неизвестных, или произведением двух разных неизвестных

F(х) = 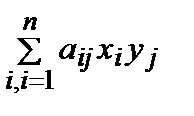. (1)

Квадратичную форму можно записать в виде F(х) = хАх, где х = (х₁, х₂, … , х_n),

А – симметрическая матрица порядка n, которая называется матрицей квадратичной формыF(х).

Две квадратичные формы называются эквивалентными, если одна из них переводится в другую посредством невырожденного линейного преобразования.

Если в квадратичной форме F(х) = х Ах неизвестные подвергнуть линейному преобразованию x = Sy, то получится квадратичная форма F(у) = у( S^TА S)y с матрицей S^TА S.

Каноническим видом данной квадратичной формы называется эквивалентная ей форма, не содержащая произведений неизвестных. Каждую квадратичную форму можно привести к каноническому виду с помощью линейного преобразования неизвестных

x = Sy с ортогональной матрицей S. Столбцами матрицы S являются координаты некоторого ортонормированного базиса B^н =(e₁ ,...,e_n), в котором матрица A имеет диагональный вид D = S^TА S. D− диагональная матрица, на диагонали которой стоят собственные числа матрицы.

Если F(х) > 0 (< 0) для всех х ≠ θ, то квадратичная форма F(х) называется положительно (отрицательно) определенной. Квадратичная форма положительно (отрицательно) определена, если в каком-нибудь ее каноническом виде нет отрицательных (положительных) коэффициентов при квадратах неизвестных.

Критерием положительной определенности квадратичной формы является следующее утверждение (критерий Сильвестра): для того, чтобы квадратичная формаА(х,х) была положительно определенной, необходимо и достаточно, чтобы все главные миноры ее матрицыАбыли положительны, т.е.D_k> 0, k = 1, 2, … ,n.

Следующие условия равносильны:

1) квадратичная форма F(х) = хАх положительно определена;

2) собственные значения матрицыА положительны;

3) угловые миноры матрицыА положительны.

Следующие условия равносильны:

1) квадратичная форма F(х) = хАх отрицательно определена;

2) собственные значения матрицыА отрицательны;

3) все угловые миноры матрицыА нечетного порядка отрицательны, а все угловые миноры четного порядка положительны.

Пример 1.Написать матрицу квадратичной формы

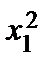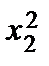F = 2 – 5 + 8 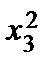+ 4x₁x₂ – 2x₁x₃ + 6x₂x₃ .

Р е ш е н и е. Обозначим коэффициент при произведении x_ix_k = x_kx_i (i ≠ k) через

а_ik + а_ki, причем а_ik = а_ki. Член (а_ik + а_ki) x_ix_k запишем в виде а_ikx_ix_k + а_kix_kx_i . Тогда квадратичную форму F можно записать в виде

F = 2 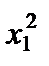+ 2x₁x₂ – x₁x₃ + 2x₂x₁ – 5 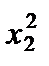+ 3x₂x₃ – x₃x₁ + 3x₃x₂ + 8 .

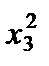Теперь матрицаАквадратичной формы имеет вид: A= 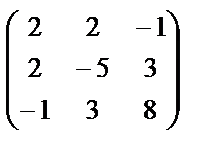.