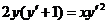Линейные дифференциальные уравнения первого порядка. Уравнения

Бернулли. Уравнение вида

у'+Р(х)у=Q(х)

называется линейным (у и у' входят в первых степенях, не перемножаясь между собой). Если Q(х)≠0, то уравнение называется линейным неоднород­ным, а если Q(x)≡0—линейным однородным.

Общее решение однородного уравнения у'+Р(х)y=0 легко получается разделением переменных:

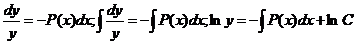
или, наконец,

,

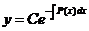где С—произвольная постоянная.

Общее решение линейного неоднородного уравнения можно найти исходя из общего решения соответствующего однородного уравнения методом Лагранжа, варьируя произвольную постоянную, т. е. полагая 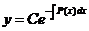, где С (х)—некоторая, подлежащая определению, дифференцируемая функция от х.

Для нахождения С (х) нужно подставить у в исходное уравнение, что приводит к уравнению

.

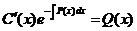Отсюда

,

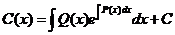где С—произвольная постоянная. Тогда искомое общее решение линейного неоднородного уравнения имеет вид

.

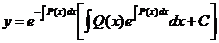Линейные уравнения первого порядка можно интегрировать также мето­дом Бернулли, который заключается в следующем. С помощью подстановки у=иv, где u и v—две неизвестные функции, исходное уравнение преобразу­ется к виду

и'v+uv'+Р(х)иv=Q(х), или и[v'+Р(х)v]+uv'=Q(х).

Пользуясь тем, что одна из Неизвестных функций (например, v) может быть выбрана совершенно произвольно (поскольку лишь произведение иv должно удовлетворять исходному уравнению), за v принимают любое част­ное решение уравнения v'+P(x)v=0 (например, 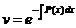), обращающее, следовательно, в нуль коэффициент при и в последнем уравне­нии.

Тогда предыдущее уравнение примет вид

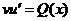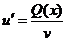, или , т.е.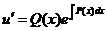

откуда

.

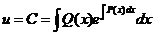Общее решение исходного уравнения находится умножением и на v.

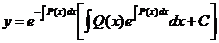
Уравнение (нелинейное) вида

у'+Р(х)у=Q(х)у''',

где от m≠0, m≠1, называется уравнением Бернулли. Его можно преобразовать в линейное уравнение, производя замену неизвестной функции при помощи подстановки z=y^1-m, в результате чего исходное уравнение преобразуется к виду

.

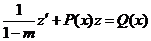При интегрировании конкретных уравнений Бернуллиих не надо пред­варительно преобразовывать в линейные, а сразу применять либо метод Бернулли, либо метод вариации произвольной постоянной.

596. Проинтегрировать уравнениеу' соs²х + у =tgx при на­чальном условии у(0)= 0.

Решение. Интегрируем соответствующее однородное уравнениеу' соs²+y=0;

разделив переменные, получим

.

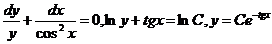Ищем решение исходного неоднородного уравнения в виде у=С(х)е^-tgx, где С (x)—неизвестная функция. Подставляя в исходное уравнение

у=С(х)е^-tgx и у'=С'(х)е^-tgx—С(х)е^-tgxseс²х,

придем к уравнению

,

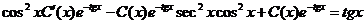или

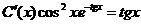
откуда

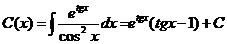
Таким образом, получаем общее решение данного уравнения:

.

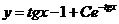Используя начальное условие у(0)=0, получим 0=-1+С, откуда С=1. Следовательно, искомое частное решение имеет вид .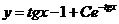

597. Проинтегрировать уравнение .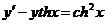

Решение. Это—линейное уравнение. Решим его методом Бернулли. Полагая у=uv, имеем

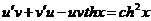,или .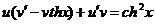

Полагаем 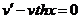, откуда 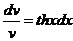; интегрируя, находим lnv=lnchx

или v=chx (постоянную интегрирования не вводим, так как достаточнонайтикакое-либо частное решение этого вспомогательного уравнения).

Для определения и имеем уравнение u’v=ch²x; или и'chx=ch² х, откуда

находим 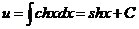. Умножение u на v, получаем общеерешение

y=chx(shx+C)

598. Проинтегрировать уравнение

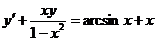
Решение. Интегрируем соответствующее однородное уравнение:

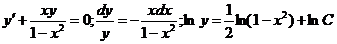
т. е. 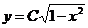. Полагаем теперь 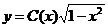; тогда

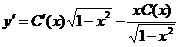
После подстановки в исходное неоднородное уравнение получим

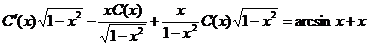
т. е.

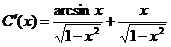
Интегрируя, находим

.

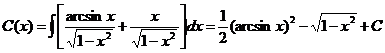Таким образом, общее решение данного уравнения имеет вид

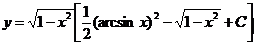
599. Решить уравнение .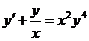

Решение. Это—уравнение Бернулли. Проинтегрируем его методом вариации произвольной постоянной. Для этого интегрируем сначала соответствующее линейное однородное уравнение 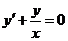, решение -которого у =С/x.

Ищем решение исходного уравнения Бернулли, полагая 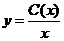', 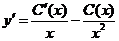. Подстановка у и у’ в исходное уравнение дает

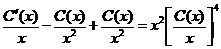или

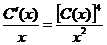
Интегрируем полученное уравнение:

;

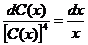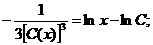
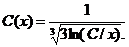
Таким образом, общее решение исходного уравнения

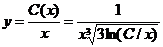
600. Проинтегрировать уравнение

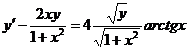
Решение. Это—также уравнение Бернулли. Проинтегрируем его методом Бер­нулли, для чего положим у=иv. Подставляя в исходное уравнение у =uv, у' =и'у+uv', сгруппируем члены, содержащие и в первой степени:

.

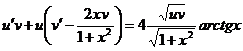Примем за v какое-либо частное решение уравнения 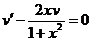. Разделяя в нем переменные, находим

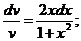
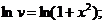
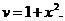
(постоянную интегрирования не вводим).

Для отыскания и имеем уравнение

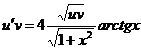
или (поскольку v=1+x²)

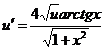
Разделяем переменные и интегрируем:

.

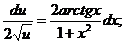
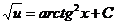Таким образом, u=(arctg²х+С)² и у=иv=(1+х²) (агсtg² х+С)² есть общее решение исходного уравнения.

601. Проинтегрировать уравнение у = ху' + y'ln у.

Решение. Данное уравнение можно легко проинтегрировать, если поменять в нем ролями х и у: принять за аргумент у, а за неизвестную функцию х. Для этого нужно только (используя формулу дифференцирования обратной функции) положить у'_х=1!х' _y. Тогда данное уравнение преобразуется в следующее:

.

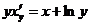Это—линейное уравнение относительно х. Интегрируем соответствующее одно­родное уравнение ух'=х, имеем

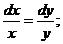x=Cy

Ищем решение исходного неоднородного уравнения, полагая х=С(у)у, откуда 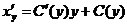. Подстановка в уравнение дает

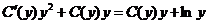, откуда .

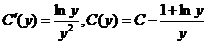Умножая С (у) на у, находим решение исходного уравнения: х= Су- 1-ln у.

602. Проинтегрировать уравнение .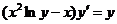

Решение. Данное уравнение можно проинтегрировать с помощью, того же преобразования, что и предыдущее. Принимая у за аргумент, х—за неизвестную функцию, преобразуем это уравнение к виду

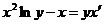, или .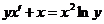

Это—уравнение Бернулли относительно x. Интегрируя, соответствующее линейное однородное уравнение ух'+х=0, находим х=С1у.

Полагаем в исходном уравнении х=C(y)/y, откуда 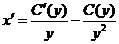; приходим к следующему уравнению для определения С (у):

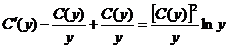, или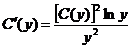

Разделяем переменные и интегрируем:

ас (у) [С (у)]2'

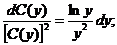
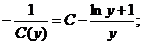
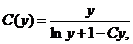
Умножая С (у) на 1/у, находим общее решение исходного уравнения:

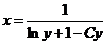
Решить уравнения:

603. .

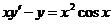604. .

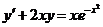605. .

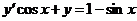606. .

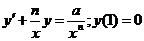607. .

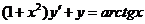608. .

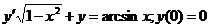609.

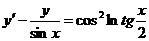
610. .

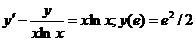611.

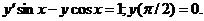
612. .

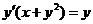●Принять за неизвестную функцию х.

613. .

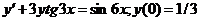614. .

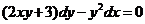● Принять за неизвестную функцию х.

615. (у⁴+2х)у'=у.

● Принять за неизвестную функцию х.

616. .

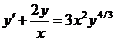617.

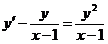
618.

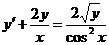
619.

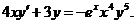
620. .

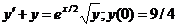621 .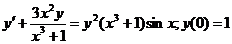

622.

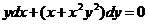
● Принять за неизвестную функцию х.

623. .

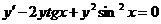624. .

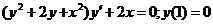● Принять за неизвестную функцию х.

7. Уравнения вида х=φ(y') и у=φ(y'). Эти уравнения легко интегри­руются в параметрической форме, если положить у'=р и принять р за па­раметр, через который следует выразить как х, так и у. В самом деле, пола­гая у'=р в уравнении х=φ(y'), сразу получаем выражение для х через па­раметр р: х=φ(р). Отсюда, дифференцируя, находим dх= φ ' (р)dр, а так как dу=у'dх=рdх, то, следовательно, dу = рφ'(р)dр и у находится интегрированием:

.

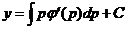Таким образом, решение уравнения x= φ(y') запишется в параметричес­кой форме:

.

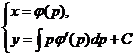Аналогично, полагаяу'=р в уравнении y= φ(y'), находим y= φ(p). Дифференцируя у, получаем dy=φ'(p)dp. Но по-прежнему dу=рdх. Таким образом, рdx= φ'(p)dp, откуда 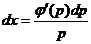и х находим интегрированием:

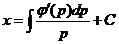
Общее решение уравнения у = φ(y') имеет вид

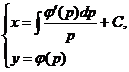
Если удается, в обоих случаях можно исключить параметр р и найти общий интеграл уравнения.

625. Проинтегрировать уравнение .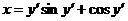

Решение. Положим у'=р. Тогда х=рsinр+соsр. Продифференцируем это равенство:

dx=(sinp+pcosp-sinp)dp=pcospdp

И подставим это значение dx в равенство dу=рdх:

,

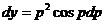т. е.

.

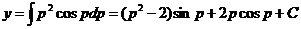Таким образом, общее решение в параметрической форме имеет вид

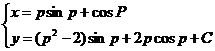
626. Проинтегрировать уравнение у'=агсtg(у/у'²).

Решение. Предварительно найдем у=у'^гtgу'• Положим у'=р; тогда у=р²tgp. Продифференцируем это равенство: dу=(2рtg р+р² sec² р)dр и, заменяя dу на рdх, получим рdх=р(2tgp+рsec² р)dр, откуда, сокращая на р и ин­тегрируя, находим

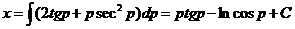
Общее решение данного уравнения имеет вид

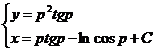
627. Проинтегрировать уравнение х=у'+lnу'.

Решение. Положим у'=р. Таким образом, х=р+lпр; дифференцируя, находим 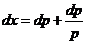. Так как dу=рdх, то

.

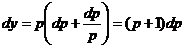Интегрируя, находим у=0,5(р+1)²+С.

Общее решение данного уравнения, записанное в параметрической форме, имеет вид

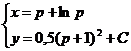
Здесь параметр р легко исключить; из второго равенства получаем 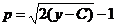(р > 0 и поэтому перед корнем надо взять знак плюс). Подставляя найденное для р выражение в первое равенство, находим общее решение уравнения в следующем виде:

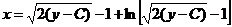
Решить уравнения:

628. .

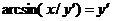629. .

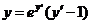630. .

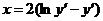631. .

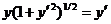632. .

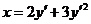633. .

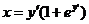634.

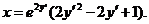
635. .

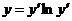8. Уравнения Лагранжа и Клеро. Уравнением Лагранжа называется диф­ференциальное уравнение первого порядка, линейное относительно х и у, коэффициентами которого служат функции от у’:

.

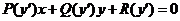Уравнение Лагранжа интегрируется следующим образом. Разрешим его относительно у и примем за параметр у', полагая у'=р:

.

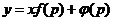[Здесь введены обозначения f(у')=-Р(y')/Q(у'), φ(у')=-R(у')/Q(у') Дифференцируя полученное уравнение и заменяя в левой части dу на pdх, приходим к уравнению

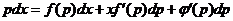
Полученное уравнение—линейное относительно х (как функции от р) и поэтому может быть проинтегрировано. Если его решение есть x=F(p,С), то общее решение исходного уравнения Лагранжа запишется в виде

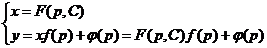
Уравнением Клеро называется уравнение вида у=ху'+φ(у'), которое является частным случаем уравнения Лагранжа. Интегрируя его указанным способом, легко получить общее решение у=Сx+φ(С), которое определяет семейство прямых на плоскости.

Однако уравнение Клеро, кроме общего решения, имеет еще и особое ре­шение, определяемое следующими параметрическими уравнениями;

.

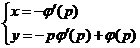Особое решение уравнения Клеро (оно существует, если φ'(р)≠const) является огибающей семейства прямых, определяемых общим решением (иными словами, общим решением уравнения Клеро служит семейство касательных ч особому решению).

Уравнение Лагранжа также может иметь особые решения, причем особыми решениями этого уравнения (если они существуют) являются общие ка­сательные ко всем интегральным кривым, определяемым общим решением.

636. Проинтегрировать уравнение у=ху'—e^y’.

Д Это—уравнение Клеро. Положим у'=р и перепишем уравнение в ви­де у=рх—е^р. Дифференцируем его: dу=рdх+хdр—е^pdp; но dу=рdх, по­этому последнее уравнение примет вид хdр—е^рdр=0, или (х—е^р)dр=0. Таким образом, либо dр=0, либо х=е^p. Если положить dр=0, то р=С; подставляя это значение р в равенство у=рх-е^р, получаем общее решение данного уравнения:

у=Сх—е^с.

Если положить х=е^p, то 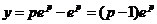, н приходим к особому решению исходного уравнения

.

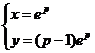Исключая параметр р (в данное случае р=lnх), находим особое решение в явном виде:

у=х(lnх—1).

Проверим, что совокупность прямых, определяемых общим решением, есть семейство касательных к особой интегральной кривой.

Дифференцируя особое решение, находим у'=lпх. Уравнение касатель­ной к особой интегральной кривой в точке М (x₀; y₀) [где y₀= x₀ (ln x₀— 1)] запишется в виде

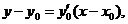или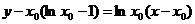

что после упрощения дает у=xlпх₀—x₀. Если здесь положить lnx₀=С, то уравнение семейства касательных к особой интегральной кривой примет вид у=Сх—e^C, что и требовалось установить.

637. Проинтегрировать уравнение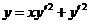

Решение. Это—уравнение Лагранжа. Поступаем аналогично предыдущему, т. е. положим у'=р, тогда у=хр²+p². Продифференцируем последнее равенство: 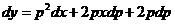. Производя замену dу=рdх, приходим к уравне­нию 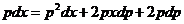. Отсюда, сокращая на р, получаем уравнение с разделяющимися переменными .

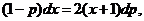или

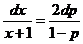
Интегрируя его, находим

ln(x+1)=-2|1-p|+lnC; x+1=С/(р—1)².

Используя данное уравнение у=р²(x+1), получим

.

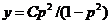Произведенное сокращение на р могло привести(и в данном случае привело) к потере особого решения; полагая р=0, находим из данного уравнения у=0: это—особое решение.

Итак,

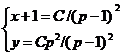— общее решение; у=0 — особое решение.

В общем решении параметр р можно исключить и привести его к виду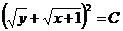

Решить уравнения:

638. 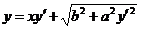. 639. .

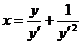640. 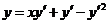641. .

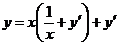642.