Исследование функций с помощью производной
1. Условия постоянства, возрастания и убывания функций
Пусть f(x) определена в V(x0).
Определение 1. Функция f называется возрастающей в точке x0, если $V(x0,d) точки x0, такая, что
f(x)<f(x0) при x<x0("xÎ(x0-d, x0),
f(x)>f(x0) при x>x0("xÎ(x0, x0+d).
Определение 2. Функция f называется убывающей в точке x0, если $V(x0,d) точки x0, такая, что
f(x)>f(x0) при x<x0("xÎ(x0-d, x0),
f(x)<f(x0) при x>x0("xÎ(x0, x0+d).
Теорема 1. Если функция f дифференцируема в точке x0 и f¢ (x0)>0 (f¢(x0)<0), то f возрастает (убывает) в точке x0.
Доказательство.
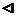 По определению производной
По определению производной 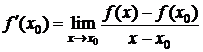 .
.
Пусть f¢ (x0)>0 (случай f¢ (x0)<0 доказывается аналогично). По определению предела функции по Коши получаем:
"e>0 (e=f¢ (x0)) $d>0: "x: |x-x0|<d выполнено 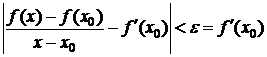 Û
Û 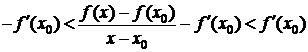 Û
Û 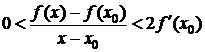 (1)
(1)
(1) выполнено 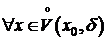 .
.
Возьмем 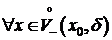 , т. е. xÎ(x0-d, x0) Þ x-x0<0. Тогда из того, что
, т. е. xÎ(x0-d, x0) Þ x-x0<0. Тогда из того, что 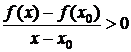 Þ f(x)<f(x0).
Þ f(x)<f(x0).
Возьмем 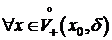 , т. е. xÎ(x0, x0+d) Þ x-x0>0. Тогда из того, что
, т. е. xÎ(x0, x0+d) Þ x-x0>0. Тогда из того, что 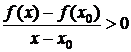 Þ f(x)>f(x0).
Þ f(x)>f(x0).
На основании определения 1 функция f возрастает в точке x0. 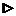
Замечание. Условие f¢ (x0)>0 (f¢ (x0)<0) не является необходимым для возрастания (убывания) функции в точке x0. Т. е. из того, что f(x) возрастает (убывает)в точке x0 не следует, что f¢ (x0)>0 (f¢ (x0)<0).
 Пример. D f(x)=x3,
Пример. D f(x)=x3, 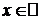 . Рассмотрим точку x=0.
. Рассмотрим точку x=0.
f¢ (x)=3x2, f¢ (0)=0, но в точке х=0 функция возрастает. D
Теорема 2 (признак постоянства функции) Пусть функция f определена и непрерывна на [a;b] и дифференцируема на (a;b). Для того, чтобы f(x) была постоянной на [a;b] необходимо и достаточно, чтобы f¢(x)=0 "xÎ(a;b).
Доказательство.
 1) Необходимость.
1) Необходимость.
Пусть f(x)=cºconst, f¢(x)=c¢=0.
2) Достаточность.
f¢(x)=0 "xÎ(a;b). Выберем "x1, x2Î[a;b]: x1<x2. К [x1;x2] применим теорему Лагранжа: $с: f(x2)-f(x1)=f¢ (c)(x2-x1), x1<c<x2. По условию f¢ (c)=0, x2-x1>0 Þ f(x1)=f(x2) "x1, x2Î[a;b], x1¹x2 Þ f(x)=cºconst. 
Следствие. Пусть f(x), g(x) определены и непрерывны на [a;b] и дифференцируемы на (a;b). Если f¢ (x)=g¢ (x)"xÎ(a;b), то f(x), g(x) отличаются друг от друга на постоянную.
Доказательство следует из теоремы 2 (применить для функции F(x)=f(x)-g(x)).
Теорема 3 (признак монотонности функции). Пусть функция f определена и непрерывна на [a;b] и дифференцируема на (a;b). Функция не убывает (не возрастает) на [a;b] Û f¢ (x)³0 (f¢ (x)£0) на (a;b).
Доказательство.
 1) Необходимость.
1) Необходимость.
Пусть f не убывает на [a;b] (случай невозрастания доказывается аналогично).
Тогда по определению "x, x0Î[a;b]: x<x0 Þ f(x)£ (x0) Þ 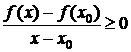 ,
,
"x, x0Î[a;b]: x>x0 Þ f(x)³ (x0) Þ 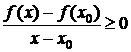 .
.
Следовательно, 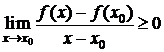 , т. е.
, т. е. 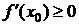 . Т. к. x0Î[a;b] - произвольная точка, то необходимость доказана.
. Т. к. x0Î[a;b] - произвольная точка, то необходимость доказана.
2) Достаточность.
Пусть f¢ (x)³0 на (a;b) (случай f¢ (x)£0 доказывается аналогично). Возьмем "x1, x2Î[a;b]: x1<x2. К [x1;x2] применим теорему Лагранжа: $сÎ( x1;x2):
f(x2)-f(x1)=f¢ (c)(x2-x1). Т. к. f¢ (с)³0, x2-x1>0, то f(x2)-f(x1)³0. Т. е. f(x2)³ f(x1). По определению функция не убывает на [a;b]. 
Теорема 4. Пусть функция f определена и непрерывна на [a;b] и дифференцируема на (a;b). Если f¢ (x)>0 (f¢(x)<0), то f возрастает (убывает) на (a;b).
Доказывается так же, как и п. 2) теоремы 3.
Замечание. Условие теоремы 4 является достаточным, а не необходимым. Например, функция y=x3 возрастает на 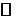 , а f¢ (0)=0.
, а f¢ (0)=0.
2. Экстремум функции
Пусть f(x) определена в V(x0).
Определение 1.Точка х=х0 называется точкой максимума функции f, если существует окрестность 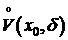 ÌV(x0), в пределах которой выполнено неравенство f(x)£f(x0).
ÌV(x0), в пределах которой выполнено неравенство f(x)£f(x0).
Значение функции в точке x0 называется максимумом функции.
Определение 2.Точка х=х0 называется точкой минимума функции f, если существует окрестность 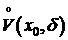 ÌV(x0): "xÎ
ÌV(x0): "xÎ 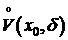 выполнено f(x)³f(x0).
выполнено f(x)³f(x0).
Значение функции в точке x0 называется минимумом функции.
Определение 3.Точка х=х0 называется точкой строгого максимума (строгого минимума) функции f, если существует 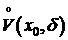 ÌV(x0): "xÎ
ÌV(x0): "xÎ 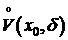 выполнено неравенство f(x)< f (x0) (f(x)>f(x0)).
выполнено неравенство f(x)< f (x0) (f(x)>f(x0)).
Значение функции в точке x0 называется строгим максимумом (строгим минимумом) функции.
Точки максимума и минимума называются точками экстремума, а значения функции в них – экстремумами функции.

 |
Можно доказать, что если функция непрерывна на (a;b) и имеет несколько максимумов и минимумов, то они чередуются. Понятия максимума и минимума являются локальными, т. е. понятиями, относящимися не ко всей области определения функции, а только к окрестности некоторой точки. Не следует смешивать понятия максимума и минимума с наибольшим и наименьшим значением функции на <a;b>. Функция f может иметь несколько максимумов (минимумов), но они не будут наибольшими (наименьшими) значениями функции. Функция может иметь наибольшее и наименьшее значения, но они не будут ни максимумом, ни минимумом.
Теорема 5 (необходимое условие экстремума). Пусть f(x) определена в V(x0). Если функция имеет в точке x0 экстремум, то производная функции в этой точке равна нулю или не существует.
Доказательство.
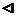 По условию функция имеет в точке x0 экстремум. Следовательно, существует окрестность
По условию функция имеет в точке x0 экстремум. Следовательно, существует окрестность 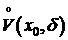 ÌV(x0), в пределах которой f (x0) является наибольшим или наименьшим значением функции f . По теореме Ферма, если существует f ¢(x0), то f ¢(x0)=0. Для завершения доказательства приведем пример, когда функция, не дифференцируемая в точке, имеет в этой точке экстремум.
ÌV(x0), в пределах которой f (x0) является наибольшим или наименьшим значением функции f . По теореме Ферма, если существует f ¢(x0), то f ¢(x0)=0. Для завершения доказательства приведем пример, когда функция, не дифференцируемая в точке, имеет в этой точке экстремум.
y=|x|, 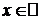 . х=0 – точка минимума, т. к. f(0)=0 и "х¹0 f(x)>0, но f(x) не дифференцируема в точке х=0.
. х=0 – точка минимума, т. к. f(0)=0 и "х¹0 f(x)>0, но f(x) не дифференцируема в точке х=0. 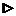
Определение. Пусть f(x) определена в V(x0). Точка x0 называется стационарной точкой функции f, если f ¢(x0)=0. Точка x0 называется критической точкой функции f, если f ¢(x0)=0 или не существует.
Из теоремы 4 следует, что точками экстремума могут быть только критические точки. Обратное не всегда верно.
Пример. D f(x)=x3, f ¢(x)=3x2, f ¢(0)=0.Но х=0 не является точкой экстремума. Действительно, при x<0 f(x)<0, а при x>0 f(x)>0. Следовательно, х=0 не является ни точкой максимума, ни точкой минимума. D
Т. о., критические точки являются точками возможного экстремума. Найдя критические точки, необходимо подвергнуть их дальнейшему исследованию.
Теорема 6 (первое достаточное условие экстремума). Пусть f дифференцируема в некоторой окрестности точки x0, кроме, быть может, самой точки x0, в которой она непрерывна. Пусть f ¢(x) сохраняет знак в отдельности как слева, так и справа от точки x0, т. е. в интервалах (x0-d; x0), (x0;x0-d). Если:
1) f ¢(x)>0 при x<x0 и f ¢(x)<0 при x>x0, то x=x0 - точка строгого максимума;
2) f ¢(x)<0 при x<x0 и f ¢(x)>0 при x>x0, то x=x0 - точка строгого минимума;
3) f ¢(x)>0 или f ¢(x)<0 "xÎV(x0), то x=x0 не является точкой экстремума.
Доказательство.
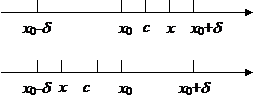
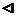 1) Возьмем "xÎV(x0,d). Применим теорему Лагранжа к отрезку [x0;x] или [x;x0]. Получим (1) f(x)-f(x0)=f¢(c)(x-x0), cÎ(x0;x) (или сÎ(x;x0)). Пусть x<x0 Þ x-x0<0. Т. к. с<x0, то f ¢(c)>0. Из (1) Þ f(x)-f(x0)<0, т. е. f(x)<f(x0). Пусть x>x0 Þ x-x0>0. Т. к. с>x0, то f ¢(c)<0. Из (1) Þ f(x)-f(x0)<0, т. е. f(x)<f(x0). Следовательно, "xÎV(x0,d) f(x)<f(x0). Значит, то x=x0 - точка строгого максимума.
1) Возьмем "xÎV(x0,d). Применим теорему Лагранжа к отрезку [x0;x] или [x;x0]. Получим (1) f(x)-f(x0)=f¢(c)(x-x0), cÎ(x0;x) (или сÎ(x;x0)). Пусть x<x0 Þ x-x0<0. Т. к. с<x0, то f ¢(c)>0. Из (1) Þ f(x)-f(x0)<0, т. е. f(x)<f(x0). Пусть x>x0 Þ x-x0>0. Т. к. с>x0, то f ¢(c)<0. Из (1) Þ f(x)-f(x0)<0, т. е. f(x)<f(x0). Следовательно, "xÎV(x0,d) f(x)<f(x0). Значит, то x=x0 - точка строгого максимума.
2) Аналогично.
3) Пусть f ¢(x)>0 "xÎ 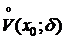 .
.
Если x<x0, т. е. x-x0<0, то из (1), т. к. f ¢(c)>0, следует f(x)-f(x0)<0, т. е. f(x)<f(x0).
Если x>x0, т. е. x-x0>0, то из (1), т. к. f ¢(c)>0, следует f(x)-f(x0)>0, т. е. f(x)>f(x0).
Следовательно, f(x0) не является ни наименьшим, ни наибольшим значением функции f(x) в 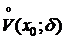 . Значит, x0 не является точкой экстремума.
. Значит, x0 не является точкой экстремума. 
Алгоритм нахождения точек экстремума для функции, непрерывной на <a;b>
Пусть f(x) на <a;b> имеет несколько критических точек. Расположим их в порядке возрастания: a<x1<x2<…<xn<b. Они делят <a;b> на интервалы (а;x1), (x1;x2),…,(xn;b). В каждом из них f ¢(x0)¹0, она знакопостоянна (положительна, или отрицательна). Для определения знака производной в интервале надо определить ее знак в любой точке интервала. Затем по изменению знака производной при переходе от одного интервала к другому определим точки экстремума по теореме 6.
Теорема 7 (второе достаточное условие экстремума). Пусть для функции f в стационарной точке x0 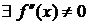 . Тогда функция имеет в точке x0 максимум, если
. Тогда функция имеет в точке x0 максимум, если 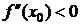 и минимум, если
и минимум, если 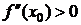 .
.
Доказательство.
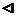 Пусть
Пусть 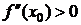 . Тогда по теореме 1 f ¢(x) возрастает в точке x0. Докажем, что x0 - точка строгого минимума. Т.к. f ¢(x0)=0, то $V(x0,d): f ¢(x)<0 при x<x0 и f ¢(x)>0 при x>x0. Тогда по теореме 5 x0 - точка строгого минимума.
. Тогда по теореме 1 f ¢(x) возрастает в точке x0. Докажем, что x0 - точка строгого минимума. Т.к. f ¢(x0)=0, то $V(x0,d): f ¢(x)<0 при x<x0 и f ¢(x)>0 при x>x0. Тогда по теореме 5 x0 - точка строгого минимума.
Для случая 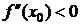 доказательство аналогично.
доказательство аналогично. 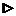
Пример.
D 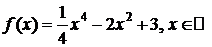
f ¢(x)=x3-4x, f ²(x)=3x2-4
f ¢(x)=0 при x1=0, x2=2, x3=-2
f ²(0)=-4 Þ x=0 – точка строго максимума, maxf(x)=f(0)=3
f ²(±2)=8 Þ x=±2 – точки строго минимума, minf(x)=f(±2)=-1. D
3. Нахождение наибольшего и наименьшего значений функции на отрезке
Пусть функция f(x) дифференцируема на отрезке [a;b]. Тогда она непрерывна на этом отрезке и, в силу II – й теоремы Вейерштрасса, достигает на нем наибольшего и наименьшего значений. Если функция имеет наибольшее значение на (a;b), то это – один из максимумов. Но функция может иметь наибольшее значение и на концах отрезка [a;b]. Аналогичные рассуждения – для минимума. Значит, для нахождения наибольшего и наименьшего значений функции на отрезке [a;b] надо:
1) найти все критические точки функции, принадлежащие отрезку [a;b];
2) вычислить значения функции в этих точках и на концах отрезка;
3) из полученных значений выбрать наибольшее и наименьшее.
4. Выпуклость функции
Пусть функция f(x) дифференцируема на <a;b>. Тогда существует касательная к графику функции f(x) в любой точке М(x;f(x)), xÎ<a;b>, причем эти касательные не параллельны оси Оу.

 Определение. Функция f(x) называется выпуклой вверх (вниз) на <a;b>, если график функции в пределах <a;b> лежит не выше (не ниже) любой из своих касательных.
Определение. Функция f(x) называется выпуклой вверх (вниз) на <a;b>, если график функции в пределах <a;b> лежит не выше (не ниже) любой из своих касательных.
Теорема 8. Пусть функция f(x) дважды дифференцируема на <a;b>. Тогда если f ²(x)³0 (f ²(x)£0) на (a;b), то функция выпукла вниз (вверх) на <a;b>.
Доказательство.
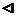 Пусть f ²(x)³0 "хÎ<a;b>. Зафиксируем произвольное х0Î(a;b). Докажем, что график функции в пределах (a;b) лежит не ниже касательной в точке М0(x0;f(x0)). Уравнение касательной:
Пусть f ²(x)³0 "хÎ<a;b>. Зафиксируем произвольное х0Î(a;b). Докажем, что график функции в пределах (a;b) лежит не ниже касательной в точке М0(x0;f(x0)). Уравнение касательной:
yкас.-f(x0)=f ¢(x0)(x-x0). (1)
Разлагая f(x) по формуле Тейлора для n=1 "хÎ(a;b), получим
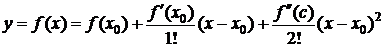 , х¹х0, х0<c<x (x<c<х0) (2)
, х¹х0, х0<c<x (x<c<х0) (2)
Вычтем (1) из (2):
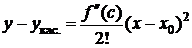 , сÎ(х0;х) (сÎ(х;х0)). (3)
, сÎ(х0;х) (сÎ(х;х0)). (3)
"хÎ(a;b) f ²(x)³0, сÎ(х0;х)Ì(a;b). Следовательно, f ²(с)³0.
Тогда из (3) следует y-yкас.³0 "хÎ(a;b), т. е. y³yкас. "хÎ(a;b). Следовательно, график функции в пределах (a;b) лежит не ниже касательной. Т. к. х0 - произвольная точка из интервала (a;b), то f(x) выпукла вниз на <a;b>. 
Пример.
D y=f(x)=x3, 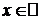
f ¢(x)=3x2, f ²(x)=6x
f ²(x)³0 при x³0 Þ на [0;+¥) функция выпукла вниз,
f ²(x)£0 при x£0 Þ на (-¥;0] функция выпукла вверх. D
5. Точки перегиба
Пусть f(x) определена и непрерывна в V(x0).
Определение.Точка x0 называется точкой перегиба функции f(x), если при переходе через эту точку меняется направление выпуклости функции f(x).
В примере х=0 – точка перегиба.
Теорема 9 (необходимое условие перегиба). Если в точке перегиба x0 функции f(x) вторая производная существует и непрерывна, то она в этой точке равна нулю.
Доказательство.
 Пусть в точке перегиба x0 существует непрерывная f ²(x0). В условиях теоремы для f ²(x0) возможны 3 случая.
Пусть в точке перегиба x0 существует непрерывная f ²(x0). В условиях теоремы для f ²(x0) возможны 3 случая.
1) f ²(x0)>0. Следовательно, т. к. f ²(x0) непрерывна, $V(x0), в которой f ²(x)>0, т. е. в точке x0 функция не меняет направления выпуклости. Значит, x0 не является точкой перегиба.
2) f ²(x0)<0. Следовательно, $V(x0), в которой f ²(x)<0. Значит, x0 не является точкой перегиба.
3) f ²(x0)=0. 
В точке перегиба вторая производная может не существовать.
Пример.
D 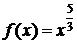 ,
, 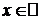 .
.
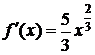 ,
, 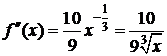 .
.
Следовательно, в точке х0=0 f ² не существует.
При x>0 f ²(x)>0 Þ на (0;+¥) функция выпукла вниз,
При x<0 f ²(x)<0 Þ на (-¥;0) функция выпукла вверх.
Значит, х0=0 - точка перегиба. D
Т. о., точками возможного перегиба являются те точки из области определения функции, в которых вторая производная равна нулю или не существует. Но не каждая такая точка является точкой перегиба.
Пример.
D y=f(x)=x4 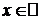
f ¢(x)=4x3, f ²(x)=12x2.
f ²(x)=0 Û х=0. Но "х f ²(x)³0, следовательно, функция выпукла вниз на 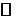 . Значит, х0=0 не является точкой перегиба, хотя f ²(x0)=0. D
. Значит, х0=0 не является точкой перегиба, хотя f ²(x0)=0. D
Т. о., точки возможного перегиба требуют дальнейшего исследования.
Теорема 10(первое достаточное условие перегиба). Пусть функция f(x) дважды дифференцируема в 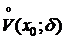 , где x0 – точка возможного перегиба. Если
, где x0 – точка возможного перегиба. Если
1) f ²(x) меняет знак при переходе через x0, то x0 - точка перегиба функции f(x);
2) f ²(x) не меняет знака при переходе через x0, то x0 не является точкой перегиба функции f(x).
Доказательство.
 1) Слева и справа от x0 функция по теореме 7 имеет разное направление выпуклости, следовательно, x0 - точка перегиба функции f(x).
1) Слева и справа от x0 функция по теореме 7 имеет разное направление выпуклости, следовательно, x0 - точка перегиба функции f(x).
2) В точке x0 функция не меняет направления выпуклости, следовательно, x0 не является точкой перегиба. 
Теорема 11.(второе достаточное условие перегиба). Если f ²(x0)=0, а 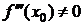 , то x0 - точка перегиба функции f(x).
, то x0 - точка перегиба функции f(x).
Доказательство.
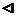 По условию
По условию 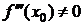 .
.
Если 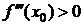 , то f ²(x) возрастает в точке x0. Т. к. f ²(x0)=0, то
, то f ²(x) возрастает в точке x0. Т. к. f ²(x0)=0, то 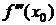 справа и слева от x0 имеет разные знаки. Тогда по теореме 9 x0 - точка перегиба.
справа и слева от x0 имеет разные знаки. Тогда по теореме 9 x0 - точка перегиба.
Если 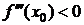 , то f ²(x) убывает в точке x0. Т. к. f ²(x0)=0, то
, то f ²(x) убывает в точке x0. Т. к. f ²(x0)=0, то 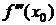 справа и слева от x0 имеет разные знаки. Следовательно, x0 - точка перегиба.
справа и слева от x0 имеет разные знаки. Следовательно, x0 - точка перегиба. 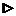
Если f ²(x0)=0 и 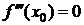 , то можно определить перегиб с помощью других достаточных условий, использующих производные высших порядков.
, то можно определить перегиб с помощью других достаточных условий, использующих производные высших порядков.
Асимптоты графика функции
Определение 1. Прямая х=а называется вертикальной асимптотой графика функции f(x), если хотя бы один из односторонних пределов функции в точке а равен +¥ или -¥.
Пример. D х=0 – вертикальная асимптота графика функции 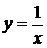 :
: 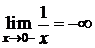 ,
, 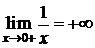 . D
. D
Определение 2. Пусть f(x) определена "x>a (x<a), 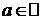 . Прямая y=kx+b называется наклонной асимптотой графика функции f(x) при х®+¥ (х®-¥), если f(x)=kx+b+a(х), где
. Прямая y=kx+b называется наклонной асимптотой графика функции f(x) при х®+¥ (х®-¥), если f(x)=kx+b+a(х), где 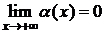
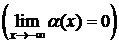 .
.
При k¹0 y=kx+b – наклонная асимптота, при k=0 прямая y=b – горизонтальная асимптота.
Теорема. Для того, чтобы прямая y=kx+b являлась наклонной асимптотой графика функции f(x) при х®+¥ (х®-¥), необходимо и достаточно, чтобы существовали 2 конечных предела:
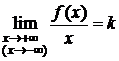 , (1)
, (1) 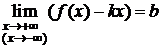 . (2)
. (2)
Доказательство.
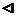 1) Необходимость.
1) Необходимость.
Пусть прямая y=kx+b – наклонная асимптота графика функции при х®+¥. Тогда по определению f(x)=kx+b+a(х), где 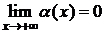 . Отсюда
. Отсюда
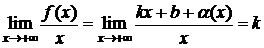 ,
,
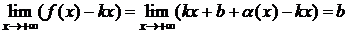 .
.
2) Достаточность.
Пусть существуют пределы (1) и (2). Из (2) следует f(x)-kx=b+a(х), где 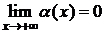 . Следовательно, f(x)=kx+b+a(х), и, значит, прямая y=kx+b является наклонной асимптотой графика функции f(x) при х®+¥.
. Следовательно, f(x)=kx+b+a(х), и, значит, прямая y=kx+b является наклонной асимптотой графика функции f(x) при х®+¥. 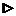
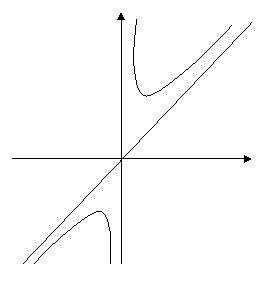
Пример. Найти асимптоты графика функции 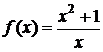 .
.
D 1) Вертикальные асимптоты.
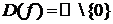 .
.
Функция является элементарной, следовательно, непрерывна в области определения, х=0 – точка разрыва. Найдем односторонние пределы в этой точке:
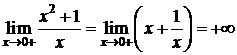 ,
, 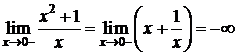 .
.
Следовательно, х=0 – точка разрыва второго рода, прямая х=0 – вертикальная асимптота графика функции.
2) Наклонные асимптоты.
1 способ (по определению). 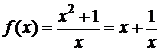 . Т. е. f(x)=kx+b+a(х), где k=1, b=0,
. Т. е. f(x)=kx+b+a(х), где k=1, b=0, 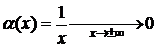 . Значит, прямая y=x – наклонная асимптота графика функции при х®±¥.
. Значит, прямая y=x – наклонная асимптота графика функции при х®±¥.
 2 способ (по теореме).
2 способ (по теореме).
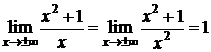 Þ k=1,
Þ k=1,
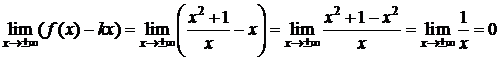 Þ b=0. Следовательно, прямая y=x – наклонная асимптота графика функции при х®±¥. D
Þ b=0. Следовательно, прямая y=x – наклонная асимптота графика функции при х®±¥. D
Схема полного исследования функции.
1. Найти область определения ( и множество значений, если просто).
2. Исследовать функцию на четность, нечетность, периодичность.
3. Исследовать функцию на непрерывность, найти точки разрыва и вертикальные асимптоты (если есть).
4. Исследовать поведение функции в окрестности граничных точек области определения и при х®±¥.
5. Найти (если есть) наклонные асимптоты графика функции.
6. Исследовать функцию на монотонность и экстремум.
7. Исследовать функцию на направление выпуклости и точки перегиба.
8. Найти точки пересечения графика функции с осями координат и промежутки знакопостоянства.
9. Построить график.
Пример. 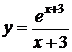 .
.
1) 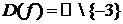 .
.
2) Функция не является ни четной, ни нечетной, не является периодической.
3) х=-3 – точка разрыва.
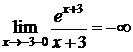 ,
, 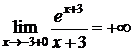 .
.
Следовательно, х=-3 – точка разрыва второго рода, прямая х=-3 – вертикальная асимптота графика функции.
4) 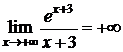 ,
, 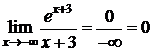 .
.
5) 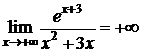 ,
, 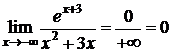 .
.
При х®-¥ k=0.
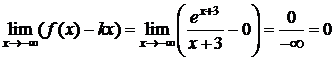 .
.
b=0 при х®-¥. Следовательно, прямая у=0 – горизонтальная асимптота графика функции при х®-¥.
При х®+¥ наклонных асимптот нет.
 6)
6) 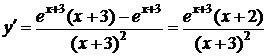 .
.
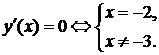
х=-2 – точка минимума, у(-2)=е – минимум.
7) 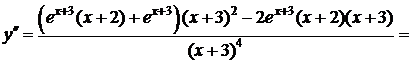
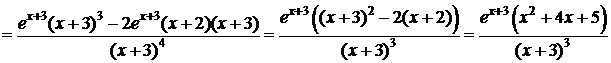
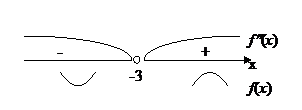
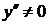 на D(f), y² не существует в точке х=-3.
на D(f), y² не существует в точке х=-3.
Точек перегиба нет.
8) Ось Ох график не пересекает.
Ось Оу: х=0, 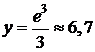 .
.
 y>0 при xÎ(-3;+¥), y<0 при xÎ(-¥;0).
y>0 при xÎ(-3;+¥), y<0 при xÎ(-¥;0).
