Частота или статистическая вероятность

Если произведена серия из п опытов, в каждом из которых могло появиться или не появиться некоторое событие А, то частотой события А (или относительной частотой)в данной серии опытов называется отношение числа опытов, в которых появилось событие А, к общему числу произведенных опытов. Частота события вычисляется на основании результатов опыта по формуле

W(A) = m/n. Где m - число появлений события А, п - общее число произведенных опытов. Частоту события часто называют его статистической вероятностью.

Сопоставляя определения вероятности и частоты события, заключаем: определение вероятности не требует, чтобы испытания производились в действительности, определение же относительной частоты предполагает, что испытания были произведены фактически. Другими словами, вероятность вычисляют до опыта, а частоту - после опыта. Длительные наблюдения показали, что если в одинаковых условиях производят опыты, в каждом из которых число испытаний достаточно велико, то относительная частота обнаруживает свойство устойчивости. Это свойство состоит в том, что в различных опытах частота изменяется мало (тем меньше, чем больше произведено испытаний), колеблясь около некоторого постоянного числа. Оказалось, что это постоянное число есть вероятность появления события.

6 ПРОТИВОПОЛОЖНЫЕ СОБЫТИЯ. Противоположныминазывают два единственно возможных события, образующих полную группу. Например, попадание и промах при выстреле по цели - противоположные события.

Для таких событий справедливо следующее утверждение: сумма вероятностей противоположных событий равна единице. Если вероятность одного из двух противоположных событий обозначена через р, то вероятность другого события обозначают через q. Таким образом, в силу предыдущего утверждения p+q=l.

Теорема (вероятность суммы несовместных событий). Если А и В несовместные события, то вероятность события Р(А+В)=Р(А)+Р(В).

Доказательство: А₁,…,А_n полная группа попарно несовместных событий.

Пусть m₁ – благоприятствует А, т₂ – благоприятствует В, т₁+т₂ следственно благоприятствует А+В, если не совместны т₁≠т₂.

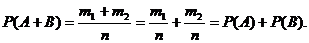
Следствие1. Вероятность наступления одного из нескольких попарно несовместных событий (безразлично какого) равна сумме вероятностей этих событий: Р(А₁+…+А_n)=Р(А₁)+…Р(А_n).

Следствие 2. Вероятность событий А равна единице минус вероятность его противоположного события 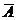: Р(А)=1-Р( 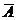). Теорема (вероятность суммы совместных событий). Вероятность наступления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий минус вероятность их совместного появления: Р(А+В)=Р(А)+Р(В)-Р(АВ).

7. Классическое определение вероятности

Вероятностью случайного события А в данном испытании называется число, обозначаемое p(A) и вычисляемое по формуле: p(a)=m/n, где n – число всех возможных элементарных событий рассматриваемого испытания, m- число тех элементарных событий из всех возможных, которое благоприятствуют появлению события А.

Ситуация, когда полную группу составляют равновозможные события, называется классической. Поэтому определение вероятности, опирающееся на такое условие называется классическим определение вероятности.

Пусть пространство элементарных событий можно отождествить с мно­жеством G точек, образующих одну из следующих геометрических фигур, — отрезок прямой или дуга кривой конечной длины, ограниченное множество на плоскости или часть поверхности конечной площади, ограниченное мно­жество в пространстве, имеющее объём, — причем по условиям опыта вероят­ность попадания в какую-либо часть множества G пропорциональна мере (длине, площади, объему) этой части и не зависит от ее расположения в G и формы. Тогда вероятность Р(А) события AcG определяется по формуле

Р(А)= мера А /мера G (геометрическая вероятность).