Операции над случайными событиями

Любые случайные события можно связать друг с другом с помощью определенных операций, получив при этом новое событие, представляющие собой некую комбинацию из исходных.

Суммой событий А и В называется событие С, которое состоит в появлении хотя бы одного из событий А и В. Например на рис.2 попадание точки в заштрихованную область означает наступление события С=A+B .

В случае, когда складываются несколько событий, суммой событий A₁, A₂, ...A_n является такое событие C, которое состоит в появлении хотя бы одного из перечисленных событий

_n

С = å A_i

ⁱ⁼¹

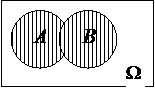а) б)

Рис.2. Сумма событий А и В – событие С, состоящее в попадании точки в заштрихованную область.

Произведение событий (их пересечение) состоит в одновременном наступлении событий А и В. Например, попадание точки в заштрихованную область рис.3 означает одновременное наступление события А – точка попала в область А и события В – точка попала в область В. Для нескольких событий их произведение – это событие, состоящее в наступление всех этих событий одновременно

_n

С = ∩ A_i

ⁱ⁼¹

Рис.3. Произведение событий A и B

Событие называется невозможным, если оно не может произойти ни при каких обстоятельствах. Такое событие обозначается символом пустого множества ø. Примером невозможного события могло бы стать событие С=AB, построенное для ситуации, изображенной на рис.2.б, поскольку в этом случае ни одна из точек не может одновременно находиться в обеих областях А и В.

Еще один особый вид события – достоверное. Достоверным является событие, происходящее при любых условиях. Для его обозначения используется символ W. В качестве примера можно рассмотреть событие, условием наступления которого является случайный выбор любой из точек области W на рис.1 (в рамках описанного для этого рисунка испытания). Если мы должны поставить любую точку в заданной области, то какую бы из точек мы не выбрали, событие, состоящее в том, что некая точка поставлена, обязательно реализуется и, следовательно, является достоверным.

События ø и W являются противоположными друг другу. В общем случае событием Ā, противоположным событию А называют событие, состоящее в непоявлении события А. Противоположное событие возникает в результате применения к событию А операции отрицания. Например, на рис.4 попадание точки в область вне области А – это событие Ā.

Рис.4. События A и Ā.

Можно написать _

Ø=W

_

W = Ø

События являются совместными, если могут произойти одновременно, то есть их произведение не является пустым множеством. Поскольку событие С=AB, изображенное на рис.2б является невозможным (С= ø), события A и B, показанные на этом рисунке являются несовместными. В то же время события A и B, показанные на рис. 2.а - совместные, так как их пересечение – не пустое множество.

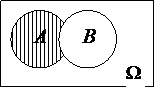Рис.5. Разность событий А и В.

На рис. 5 показана разность событий А и В, которая обозначается как А\В. Данное событие состоит в появлении события А при условии непоявления события B.

Рис. 6 поясняет определение «событие В влечет за собой событие А». В данной ситуации, обозначаемой как В Ì А, наступление события В означает обязательное наступление события А.

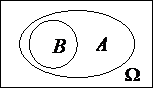Рис. 6. Множество B является подмножеством множества A.

Если события являются попарно несовместными (взаимоисключающими) и в совокупности охватывают все возможные исходы испытания, они образуют полную группу. Иначе говоря, события A₁, A₂, ...A_n образуют полную группу, если для любых двух событий A_i и A_j

A_i× A_j = ø

и

A₁+A₂+ ...+A_n=W

Событиями, образующими полную группу, являются

___

А\В, B, A+B

(см. например рис.2.) Полную группу также образуют события Ā и А, поскольку

A×Ā = ø

А+Ā=W

С помощью таких действий как отрицание, нахождение суммы или произведения, можно конструировать выражения, соответствующие неким новым событиям. В качестве примера рассмотрим три совместных события А, В и С и построим выражение для события D, которое состоит в том, что:

а) произошло только событие A

_ _

D =A×B×C

б) произошли только события A и B

_

D =A×B×C

в) произошли все три события

D =A×B×C

г) произошло хотя бы одно событие

D =A+B+C

д) произошло только одно событие

_ _ _ _ _ _

D =A×B×C+ A×B×C+ A×B×C

е) ни одного события не произошло

_ _ _ ______

D =A×B×C= A+B+C

ж) не произошло появления всех трех событий одновременно

_____

D = A×B×C

з) произошло два события

_ _ _

D =A×B×C+ A×B×C+ A×B×C

и) произошло не менее двух событий

D =A×B+A×C+B×C