Элементарные понятия теории вероятности.

Вероятность событий

Элементарные понятия теории вероятности.

Один из способов изучать окружающий мир состоит в том, чтобы проводить наблюдения (или опыты) и регистрировать количественные значения величин, описывающих то или иное явление. Если при многократной регистрации результат каждого конкретного измерения отличается от остальных (пусть даже и незначительно) и не может быть предсказан заранее с абсолютной точностью, говорят, что результат измерения является величиной случайной. Примеры случайной величины - номер выигрышного лотерейного билета, количество попаданий в цель у стрелка на соревнованиях, количество опазданий студента за семестр и т.д. Для работы со случайными величинами был создан специальный математический аппарат, который был обоснован и описан в рамках теории вероятности.

Важными понятиями в теории вероятности являются понятия испытания, исхода испытания и случайного события. Будем использовать термин испытание для таких процедур как опыт, наблюдение, измерение. Результат проведенного опыта будем называть исходом испытания. Будем считать, что испытание можно повторить неограниченное число раз, причем появление каждого из возможных исходов испытанияявляется случайным событием и не может быть предсказано заранее. Как правило, именно с конкретным исходом испытания связывают определенное значение случайной величины. В качестве примера рассмотрим испытание, которое состоит в однократном броске игральной кости в виде кубика с числом очков на гранях от 1 до 6. Случайными событием (или исходом испытания) может быть выпадение той или иной грани кубика, связанной с ним случайной величиной – количество очков на грани.

Исходы испытания называются элементарными, если взаимно исключают друг друга, в совокупности охватывают все возможные случаи (так, как это происходит в только что приведенном примере) и не могут быть представлены в виде комбинации более простых. Они могут быть равновозможными или неравновозможными (например известно, что конструкция кубика «усовершенствована» и одна из граней выпадает чаще остальных).

Можно ввести понятие пространства элементарных исходов, обозначив его греческой буквой W . Пространство элементарных исходов - это произвольное множество, элементам которого поставлены во взаимно-однозначное соответствие элементарные исходы данного испытания. Например, для испытания, состоящего в подбрасывании игральной кости можно построить пространство элементарных исходов, соответствующих выпадению грани с определенным числом очков, в виде W={1, 2, 3, 4, 5, 6}.

Отдельные исходы испытания или их комбинации всегда являются подмножеством множества элементарных исходов W. Рассмотрим еще один пример. Пусть испытание, состоит в указании определенной точки внутри заданной области, причем выбор точки осуществляется случайным образом. Выберем область в виде прямоугольника, как это показано на рис.1.

Рис.1. Множество элементарных исходов W испытания, состоящего в случайном выборе точки внутри прямоугольной области и событие А.

Множество всех точек прямоугольника – это W. Кроме элементарных исходов можно рассмотреть их комбинации. Например рассмотрим событие A, состоящее в попадании точки в область А (рис.1). Множество точек области А образует подмножество множества W.

Формулы комбинаторики

Один из способов определения вероятности случайного события состоит в непосредственном вычислении в соответствии с классическим определением. При этом необходимо уметь правильно находить число благоприятных исходов m_A и число всех исходов испытания n. При решении таких задач может оказаться полезным применение формул комбинаторики.

Основной принцип, на котором строятся все расчеты – это принцип умножения. Он формулируется следующим образом. Пусть необходимо выполнить одно за другим k действий. Первое можно выполнить n₁ различными способами, второе – n₂ различными способами, третье – n₃ различными способами и т.д. В этом случае все k действий могут быть выполнены n₁×n₂×n₃....×n_k различными способами.

Рассмотрим в качестве примера задачу о броске двух игральных костей, в которой необходимо найти число возможных выпавших комбинаций. На первой кости грань может выпасть одним из 6 способов, на сторой – аналогично. Следовательно, число комбинаций 6×6=36.

Пусть известно, что номер телефона состоит из 6 цифр, каждая может быть любой (от 0 до 9). Согласно принципу умножения число возможных комбинаций 10×10×10×10×10×10=10⁶. Таким образом, вероятность набрать правильный номр случайно равна 1/1 000 000.

Рассмотрим задачу о телефонном номере, но при условии, что все цифры телефонного номера должны быть разными. Теперь у нас в запасе 10 цифр и каждую можно использовать только 1 раз. Таким образом, первую цифру можно набрать одним из 10 возможных способов, вторую – уже только девятью, так как одну из 10 цифр мы уже использовали, третью – только восьмью и т.д. Число комбинаций 10×9×8×7×6×5=151200.

В последнем примере мы неявно использовали формулу для подсчета числа размещений. Размещение – это упорядоченный набор из k элементов, выбранных из n имеющихся. О размещении говорят, когда необходимо заполнить k позиций любыми из имеющихся n элементов. Чтобы задать размещение из k элементов, необходимо на первое место поместить один из этих элементов. Это можно сделать n способами. На второе место можно поместить следующий элемент. Это возможно сдедать n-1 способами. Следующий элемент мы сможем выбрать n–2 способами, на позицию k элемент поместим
n– (k-1) числом способов. Таким образом, число размещений определяется по формуле

A_n^k=n×(n-1)×(n-2)×...×(n-(k-1)=n!/(n-k)!

Напомним, что для любого натурального числа m!=1×2×3×...×m . Кроме того, согласно принятому правилу 0!=1

Частным случаем формулы для подсчета числа размещений является формула для подсчета числа перестановок. Ее можно получить, приравняв число позиций к числу элементов, то есть положив k=n. Перестановка - упорядоченный набор n элементов из n возможных. Число способов переставить n элементов местами равно

P_n=n×(n-1)×(n-2)×...×1=n!

В качестве примера рассмотрим следующую задачу. Пусть к вам пришли три гостя, и у вас для них есть три места. Необходимо определить число сопособов, которыми можно рассадить гостей. Поскольку n=3, P_n=3!=6.

Разновидностью формулы для подсчета перестановок является формула для подсчета числа перестановок с повторениями. Предположим, что есть n элементов, но n₁ из них принадлежат к сорту 1, n₂ – к сорту 2, n_k – к сорту k. Элементы, принадлежащие к одному сорту, неразлечимы между собой в каждой конкретной перестановке. В этом случае число возможных перестановок необходимо рассчитывать по формуле

P_n1n2...nk = n!/(n₁!×n₂! ×n₃!×...×n_k!)

Предположим, необходимо посчитать число различных перестановок для трех шаров, два из которых – одного цвета. Если каждому шару присвоить свой уникальный номер – перестановок будет 6. Если учитывать только цвета шаров, то любые две перестановки, в которых одинаковые по цвету шары меняются местами будут считаться одним и тем же результатом, то есть перестановок окажется в два раза меньше. Проверим это с помощью формулы. Число шаров первого сорта равно2 число шаров второго сорта равно 1. P₂₁ = 3!/(2!×1!)=3.

Еще одной важной формулой комбинаторики является формула для подсчета числа сочетаний. Сочетанием из n элементов по k называется любой неупорядоченный набор k элементов, выбранных из n имеющихся. Формулу для числа сочетаний легко получить из формулы для размещений. Посокольку набор k элементов не должен быть упорядочен, все размещения с определенным набором k элементов (k! штук) относятся к одному и тому же сочетанию. Следовательно, сочетаний должно быть в k! раз меньше.

С_n^k= n!/(n-k)!/ k!

Рассмотрим еще один пример. Пусть необходимо выбрать трех человек из присутствующих пяти в любом порядке. Для определения числа возможных комбинаций воспользуемся формулой сочетаний С₅³=5!/(5-3)!/3! =10. Если необходимо не просто выбрать людей, но и разместить их в определенном порядке, число возможных комбинаций будет больше - A₅³=5!/(5-3)!=10×3!=60, так как три объекта всегда можно разместить шестью способами.

Напомним, что выражение для числа сочетаний С_n^k на самом деле является биномиальным коэффициентом, то есть входит в формулу бинома Ньютона

_n

(a+b)ⁿ= С_nⁿaⁿb⁰+ С_n^n-1a^n-1b¹+...+ С_n⁰a⁰bⁿ=å С_n^ka^kb^n-k

^k=0

В частности, (a+b)²= С₂²a²b⁰+ С₂¹a¹b¹+С₂⁰a⁰b²=a²+2ab+b².

Последней формулой, которую мы рассмотрим, является формула сочетаний с повторениями. Сочетанием из n элементов по k c повторениями называется неупорядоченный набор из k элементов, каждый их которых принадлежит к одному из n возможных типов. Пусть, например, у нас есть элементы трех сортов - A, B и C. Поскольку речь идет не о конкретном элементе, а о сорте, элемент может входить в сочетание несколько раз. Например, сочетания по два элемента, кроме обычных сочетаний AB, AC, BC, будут включать и AA, BB, CC. В случае, когда рассматривается сочетание из трех элементов, возможны комбинации ABC, AAA, BBB, CCC, AAB, AAC, ABB, ACC, BBC, BCC. Формула для подсчета сочетаний с повторениями записывается как:

f_n^k= С_p^q,

где p=n+k-1, q=n-1 или q=n.

Вероятность суммы событий

Рассмотрим два совместных события A и B с вероятностями P(A) и P(B) на пространстве элементарных исходов W (рис.3). Сумму этих событий можно записать в виде

A+B=A\AB+B\AB+AB.

Напомним, что выражение A\AB (разность событий) означает, что событие А произошло но не произошло событие АВ.

Вероятность суммы событий можно вычислить, используя геометрическое определение. Очевидно, что площадь фигуры A+B

s_A+B=s_A\AB+ s_B\AB+ s_AB= s_A+ s_B- s_AB

и

P(A+B)= P(A/AB)+ P(B/AB)+ P(AB)= P(A)+ P(B)- P(AB)

Таким образом, для совместных событий

P(A+B)= P(A)+ P(B)- P(AB)

В случае несовместных событий P(АВ)=0 и

P(A+B)= P(A)+P(B)

В качестве примера найдем вероятность события A+B , если известно, что P(A)=0.2, P(B)=0.6, а P(AB)= 0.08. Подставив данные в формулу, получим P(A+B)=0.72.

Решим пример при условии, что события A и B имеют те же вероятности, но являются независимыми: P(A+B)=0.2+0.6-0.12=0.68.

В случае, если событий несколько и они совместны, выражение для суммы усложняется. Так для трех совместных событий A, B и С:

P(A+B+С)= P(A)+P(B)+P(С)- P(AB) - P(AС) - P(BС)+ P(ABС)

Если рассмотреть события A₁, A₂, ...A_n, образующие полную группу (попарно несовместные и в сумме дающие достоверное событие), вероятность их суммы будет равна

P(A₁+ A₂+ ...+A_n)= P(A₁)+ P(A₂)+ ...+ P(A_n)= P(W)=1

В частном случае, для событий Ā и А

P(A+ Ā )= P(A)+ P(Ā)= P(W)=1

и

P(Ā)=1- P(A)

Таким образом, вероятность события, противоположного данному, всегда можно найти, если известна вероятность самого события.

Рассмотрим пример. Стрелок попадает в первое кольцо мишени с вероятностью 0.5, во второе – с вероятностью 0.3, в центр – с вероятностью 0.1 Необходимо найти вероятность промаха. Поскольку события, связанные с попаданием в мишень несовместны, мы можем найти вероятность события, противоположного промаху, которое состоит в том, что стрелок попал в мишень P(Ā)=0.5+0.3+0.1=0.9. Тогда вероятность искомого события P(A)=1-0.9=0.1.

Если события A₁, A₂, ...A_n независимы, вероятность их суммы можно определить по формуле

___________ _ _ _

P(A₁+ A₂+ ...+A_n)=1- P(A₁+ A₂+ ...+A_n)= 1- P(A₁×A₂× ...×A_n)=

_ _ _

= 1- P(A₁)×P(A₂)× ...× P(A_n)

Формула Бернулли

Пусть последовательно проводятся n одинаковых независимых испытаний, в каждом из которых событие A может произойти с вероятностью P(A)=p. Вероятность того, что событие A не произойдет P(Ā)=1-p=q.

По сути дела, речь идет о том, чтобы случайным образом заполнить n возможныхпозиций событиями A и Ā. Например, результат серии испытаний может быть таким: A Ā A Ā A ... Ā. Число возможных исходов каждого независимого испытания - два (A и Ā), всего испытаний n, и, согласно принципу умножения, число различных последовательностей, состоящих из событий A и Ā равно 2ⁿ.

Поскольку все испытания независимы, вероятность каждого общего результата для серии n испытаний определяется как произведение вероятностей отдельных исходов. Например, вероятность того, что событие A появится во всех n случаях составляет pⁿ. Вероятность того, что неудача произойдет только в первом испытании равна p^n-1q. Вместе с тем, результатов с одной неудачей может быть n=C_n¹ и вероятность события «в n испытаниях n-1 раз появилось событие A» составляет C_n¹p^n-1q. В общем случае, вероятность того, что в серии n независимых испытаний событие A появится k раз дается формулой Бернулли:

P_n(k)=C_n^kp^kq ^n-k,

где 0£k£n.

Вероятности P_n(k) называются биномиальными, поскольку
C_n^kp^kq ^n-k – общий член разложения бинома Ньютона.

_n

(p+q)ⁿ=SC_n^kp^kq ^n-k

^k=0

Поскольку p+q=1, то

_{n n}

SP_n(k) = SC_n^kp^kq ^n-k=1

^{k=0 k=0}

Рассмотрим следующий пример. Пусть известно, что число стальных деталей в партии в два раза больше, чем число чугунных. Необходимо найти вероятность того, что из трех наудачу взятых деталей 2 окажутся стальными. В этой задаче вероятность того, что наудачу выбранная деталь окажется стальной p=2/3, вероятность противоположного события q=1/3 и

P₃(2)=C₃²(2/3)²(1/3) ¹=4/9=0.444

2.2 Наивероятнейшее число появлений успеха в n независимых испытаниях.

Зафиксируем значения n, p и q. В этом случае вероятность P_n(k) можно рассматривать как функцию k. Например при n=3

P₃(0)=C₃⁰p⁰q ³= q ³

P₃(1)=C₃¹p¹q ²=3pq ²

P₃(2)=C₃²p²q ¹=3p²q

P₃(3)=C₃³p³q ⁰=p³

Если построить значения вероятности на графике для определенных p и q, можно будет увидеть, какому числу успехов k соответствует максимальное значение вероятности P₃(k).

Найдем k, при котором P_n(k) принимает максимальное значение в общем случае. Можно показать, что отношение

P_n(k+1) /P_n(k) =(n-k)p/(k+1)/q

Следовательно, P_n(k+1) > P_n(k) при условии (n-k)p > (k+1)/q. Перепишем последнее неравенство как np-q > k(p+q)= k. Когда знак неравенства меняется, значение вероятности начинает убывать с ростом k. Равенство P_n(k+1) = P_n(k), соответствующее максимальному значению вероятности, реализуется при условии k=k₀=np-q и k+1=k₀+1=np-q +1=p(n+1). Данное равенство возможно только в случае, если np-q - целое число. В случае, когда np-q является дробным, к его целой части необходимо прибавить единицу - k₀=[np-q] +1 , то есть в качестве k₀ берется наименьшее целое значение k, превосходящее np-q. В этом случае наблюдается только одно максимальное значение P_n(k₀).

Пусть необходимо найти наиболее вероятное число выпадений герба при 20 и 25 бросках монеты. В этой задаче p =q=0.5. При n =20 np-q =10-0.5=9.5, k₀=[9.5] +1=10. При n =25 np-q = 12.5-0.5=12, k₀=12, k₀+1=13.

Обобщение формулы Бернулли

Пусть последовательно проводятся n одинаковых независимых испытаний, однако исходов каждого испытания теперь не два, а m - A₁, A₂, ...A_m, m>2. Согласно принципу умножения число число различных последовательностей длиной n, состоящих из событий A_iравно m ⁿ.

Чтобы построить последовательность событий, случайным образом реализовавшихся в n испытаниях, необходимо на n позициях разместить элементы A_i, среди которых какое-то количество (обозначим его k₁) относится к “первому сорту” (A₁), какое-то количество (k₂)– ко “второму сорту” (A₂), а какое-то (k_m) – к “сорту m ” (A_m). При заданных значениях k₁, k₂, ... k_m вероятность реализации конкретной последовательности равна p₁^k1p₂^k2 ...p_m^km (p_i - вероятность появления исхода A_i). Если же учесть все возможные перестановки при заданных k₁, k₂, ... k_m (см. формулу для перестановки с повторениями), для вероятности события, состоящего в том, что в n независимых испытаниях событие A₁ появится k₁ раз, A₂ - k₂ раз, A_m - k_m раз, получим

P_n(k₁, k₂, ... k_m) = n!/(k₁!×k₂!×k₃!...×k_m!)×p₁^k1p₂^k2...p_m^km

Формула Пуассона

Рассмотрим n независимых одинаковых испытаний. Пусть число исходов одного испытания m=2 (A и Ā), вероятность появления события A равна p. Введем константу l=np и найдем предел, к которому стремиться вероятность P_n(k)=C_n^kp^kq ^n-k при бесконечно большом числе испытаний

P_n(k)=C_n^kp^kq ^n-k= n!/(n-k)!/k!(l/n)^k(1-l/n)^n-k=

=l^k/k!×n(n-1)(n-2)(n-(k-1))/n^k××(1-l/n)^-k(1-l/n)ⁿ®=l^k/k!×1×1×e^-l

^n®¥

Таким образом,

lim P_n(k)= l^k/k!×e^-l

^n®¥

Данная выражение называется формулой Пуассона. С ее помощью можно вычислять приближенное значение вероятности появления k успехов в n одинаковых независимых испытаниях, при условии, что n достаточно велико, а вероятность мала (n³100, p£0.1).

Рассмотрим пример. Пусть одна рыба ловится в среднем при 200 забрасываниях удочки. Какова вероятность поймать хотя бы одну рыбу при 100 забрасываниях. n=100, p=1/200=0.05, l=np=0.5

Противоположным событием для события “поймана хотя бы одна рыба” является событие “не поймано ни одной рыбы” Его вероятность P₁₀₀(0)= C₁₀₀⁰×0.5⁰×0.955 ¹⁰⁰=0.955 ¹⁰⁰ »l⁰/0!×e^-l= e^-0.5

Таким образом, искомая вероятность, вычисленная с помощью формулы Пуассона P_n(k³1)»1- e^-0.5=0.39347. Точный результат, полученный с помощью формулы Бернулли P_n(k³1)=1- 0.955 ¹⁰⁰ =0.39423

Локальная теорема Лапласа.

Применять формулу Бернулли при достаточно больших значениях n может быть затруднительно, так как в этом случае требуется проводить вычисления для очень больших чисел. Например при n=50, k=30, p=0.2 вероятность появления успехов в 30 испытаниях P₅₀(30)=50!/(30!×20!)×0.2³⁰×0.8²⁰ и входящий в выражение факториал 20!=2432902008176640000. В таких случаях удобно использовать приближенные вычисления. Кроме формулы Пуассона существует еще несколько выражений для приближенного определения вероятности. К числу принадлежит локальная теорема Лапласа. О том, как ее можно доказать, мы поговорим позднее, а пока просто познакомимся с результатами. Согласно данной теореме, если вероятность p появления события A в каждом испытании постоянна и отлична от 0 и 1, то вероятность появления события A в n испытаниях ровно k раз при достаточно больших значениях n

P_n(k)»1/(npq)^0.5×1/(2p)^0.5×e^-x2/2=1/(npq)^0.5×j(x)

Функция j(x)= 1/(2p)^0.5×e^-x2/2 является четной, то есть j(x)= j(-x),
x=(k-np)/(npq)^0.5. Значения функции j(x) затабулированы, поэтому при решении задач достаточноопределить x и, используя таблицы, найти искомую вероятность. Пусть, например, n=400, k=80, p=0.2, q=1-p=0.8. Найдем x=80-400×0.2/(400×0.2×0.8)^0.5=0, j(0)=0.3989 и P₄₀₀(80)»1/8×0.3989=0.0498.

Биномиальное распределение

Случайная величина X называется распределенной по биномиальному закону, если она принимает значения 0, 1, 2, ...n, вероятность которых вычисляется по формуле p_k=p(X=k)= C_n^kp^kq ^n-k, 0£k£n, q=1-p, 0£p£1. Распределение полностью определяется двумя параметрами – p и n. Примером биномиального распределения может являться задача о числе выпавших гербов при броске n монет. Если k - число гербов, вероятности k успехов в n испытаниях можно определить по формуле Бернулли P_n(k)=C_n^kp^kq ^n-k.

Распределение Пуассона

Дискретная случайная величина имеет распределение Пуассона, если ее возможные значения X={0, 1,2,...k, ...}, вероятности которых вычисляются по формуле Пуассона p_k=p(X=k)=l^k/k!×e^-l,
k=0,1,2,3, ..., np=l=const.

Основные свойства дисперсии

1. Дисперсия константы равна нулю.

D(C)=M([C-M(C)]²)= M([C-C]²)=0

2. Дисперсия произведения случайной величины на констану равна квадрату константы умноженному на дисперсию случайной величины

D(СX)=M([СX-M(СX)]²)=M([СX-СM(X)]²)=

=M(С²×[X-M(X)]²)=С²×D(X)

3. Дисперсия суммы двух независимых случайных величин равна сумме их дисперсий. Если величины зависимы, к сумме дисперсий необходимо добавить удвоенную ковариацию этих величин.

Прежде чем доказывать это свойство, введем новую величину, которую назовем ковариацией. Определение этой величины мы рассмотрим позднее, а пока запишем для нее следующее равенство:

Cov(X, Y)=M(X×Y)-M(X)×M(Y)

В случае, если величины независимы,

M(X×Y)=M(X)×M(Y)

и

Cov(X, Y)=0

Докажем, что в общем случае

D(X+Y)= D(X)+ D(Y)+2 Cov(X, Y)

Для доказательства воспользуемся рассмотренной выше теоремой для дисперсии и свойствами математического ожидания:

D(X+Y)= M([X+Y]²)-[M(X+Y)]²= M([X²+Y²+2×X×Y])-[M(X)+M(Y)]²=

= M(X²)+M(Y²)+2×M(X×Y)-[(M(X))²+(M(Y))²+2×M(X)×M(Y)]=

=[M(X²)-(M(X))²]+[M(Y²)-M(Y))²]+2×(M(X×Y)- M(X)×M(Y))=

= D(X)+D(Y)+2 Cov(X, Y)

Для независимых случайных величин

D(X+Y)= D(X)+D(Y)

Аналогичное свойство можно записать и для нескольких случайных величин. Рассмотрим величины X₁, X₂, ..., X_n c дисперсиями D(X₁), D(X₂) ...,D(X_n) и математическим ожиданиями M(X₁), M(X₂) ..., M(X_n). Известно, что

M(X₁+X₂+ +X_n)= M(X₁)+M(X₂)+...+ M(X_n)

Рассмотрим

D(X₁+X₂+ +X_n)=M([ (X₁+X₂+...+ X_n)- M(X₁+X₂+...+ X_n)]²)=

=M([X₁- M(X₁)+X₂- M(X₂)...+ X_n- M(X_n)]²) =

=M[(X₁- M(X₁))²+(X₂- M(X₂))²+...+(X_n- M(X_n))²+

+2×(X₁- M(X₁))×(X₂- M(X₂))+...+2×(X_n-1- M(X_n-1)) ×(X_n- M(X_n))]=

=SD(X_i)+ 2×SCov(X_i, X_j),

^{i i>j}

4. Используя доказанное выше свойство для дисперсии суммы двух случайных величин можно показать, что дисперсия суммы случайной величины и константы равна дисперсии этой случайной величины, то есть дисперсия не меняется при смещении всех значений случайной величины на одну и ту же константу.

D(X+С)= D(X)+ D(С)= D(X)

5. Для среднего арифметического n случайных величин, имеющих одинаковое распределение с математическим ожиданием M(X_i)=a, D(X_i)=d, дисперсия уменьшается в n раз

_

D(X)= D((X₁+ X₂+...+ X_n)/n)=1/n²×( D(X₁)+ D(X₂)+...+ D(X_n))/n=

=nd/n²=d/n

Исходя из этого свойства можно утверждать, что при многократных измерениях одной и той же характеристики, среднее значение нескольких измерений будет точнее описывать ее истинную величину, чем одно отдельное измерение, так как отклонение от математического ожидания (ошибка измерения) тем меньше, чем больше число измерений.

6. Дисперсия случайной величины X, равной числу появлений события A в n независимых испытаниях, в каждом из которых вероятность появления события A равна p, D(X)=npq, где q=1- p.

Можно показать, что для переменной X₁ с законом распределения

	xk pk 1-p p

X₁

M(X₁)=0×(1-p)+ 1×p=p

и

D(X₁)= M([X₁]²)-[M(X₁)]²=1²×p+0²(1-p)- p²= p- p²= p (1-p)= pq

Случайная величина

X= X₁+ X₁+... X₁

^{n раз}

и

D(X)=D(X₁+ X₁+... X₁)= pq+ pq+...+ pq= npq

Математическое ожидание

Математическим ожиданием непрерывной случайной величины называется интеграл плотности вероятности

_¥

M(x)= ∫ xf(x)×dx

^-¥

В случае, если функция плотности вероятности отлична от нуля только на интервале a<x<b

_b

M(x)= ∫ xf(x)×dx

^a

Дисперсия

Дисперсией непрерывной случайной величины называют математическое ожидание отклонения случайной величины от ее математического ожидания

_¥

D(x)= ∫[x-M(X)]²×f(x)×dx

^-¥

В случае, если функция плотности вероятности отлична от нуля только на интервале a<x<b

_b

D(x)= ∫[x-M(X)]²× f(x)×dx

^a

Для дисперсии и математического ожидания непрерывной случайной величины выполняются те же свойства, что и для дискретной.

Мода и медиана

Модой непрерывной случайной величины X называют такое значение x_Mo=x₀, для которого функция плотности распределения f(x₀)× максимальна.

Медианой непрерывной случайной величины X называют такое значение x_Me=x₀, для которого функция распределения равна 0.5

P(X< x_Me)= P(X> x_Me)= F(x_Me)=0.5

5.3.4. Моменты k-го порядка

Начальным моментом k-го порядка непрерывной случайной величины X называется математическое ожидание величины величины X^k

_¥

a_k (X)=M(X ^k)= ∫x^k f(x)×dx

^-¥

Центральным моментом k-го порядка непрерывной случайной величины X называется математическое ожидание k-ой степени соответствующей центрированной величины.

_{· ¥}

M_k(X)=M(X ^k)= ∫[x-M(X)]^k×f(x)×dx

^-¥

Асимметрия и эксцесс.

Для характеристики общего вида графика плотности вероятности случайной величины вводят такие параметры, как асимметрия и эксцесс.

Для оценки асимметрии распределения случайной величины можно использовать любой нечетный центральный момент, если его порядок выше первого. Обычно используется нормированный третий момент случайной величины

as=m³/s³=1/s³×M([X-M(X)]³)

При as>0 асимметрия положительна и более длинное крыло кривой распологается справа от математического ожидания. При as<0 асимметрия отрицательна и «длинна часть» кривой распологается слева от математического ожидания. Для симметричного распределения as=0.

Эксцесс теоретического распределения вводится как

Ek=m⁴/s⁴-3.

Если случайная величина распределена в соответствии с нормальным законом, Ek=0. При Ek<0 – функция плотности распределения имеет более низкую и плоскую вершину, чем в случае нормального распределения, при Ek>0 – более высокую и острую вершину.

Равномерное распределение

Распределение называется равномерным, если плотность вероятности постоянна на интервале a<x<b и равна 0 вне интервала.

0, x£a

f(x)= 1/(b-a), a<x£b

1, x>b

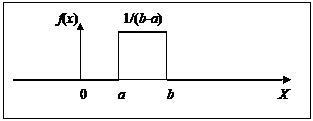Рис. 8. Равномерное распределение (плотность распределения)

Пользуясь свойствами функции распределения легко показать, что

При x£a функция

_x

F(x)= P(-¥<X< x)= ∫ f(t)×dt=0

^-¥

При a<x£b функция

_0x

F(x)=P(-¥<X<x)= ∫ f(t)×dt + ∫ f(t)×dt=x/(b-a)

^{-¥ a}

При x>b F(x)=P(-¥<X< x)=1

_{0 b x b}

F(x)=P(-¥<X<x)= ∫ f(t)×dt + ∫ f(t)×dt +∫ f(t)×dt =∫1/(b-a)dx=(b-a)/(b-a)=1

^{-¥ a b a}

Таким образом,

0, x£a

F(x)= (x-a)/(b-a), a<x£b

1, x>b

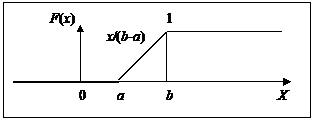Рис. 9. Равномерное распределение (функция распределения)

Математическое ожидание для равномерного распределения

_{b b b}

M(x)= ∫ xf(x)×dx=∫1/(b-a) xdx=1/2×x²/(b-a)½=(b²- a²)/(b-a)/2=(a+b)/2

^{a a a}

Дисперсия равномерного распределения

_b

D(X)=M([X]²)-[M(X)]²=∫x²/(b-a)dx-[(b+a)/2]²=(b-a)²/12

^a

Мода для равномерного распределения не существует, медиана x_Me==(a+b)/2.

Показательное распределение

Показательное распределение задается функцией

le^-lx, x³0

f(x)=

0, x<0

Функция распределения

1-e^-lx, x³0

F(x)=

0, x<0

Зная функцию распределения легко определить вероятность попадания случайной величины в заданный интервал

P(a<x<b)= F(b)- F(a)= e^-la- e^-lb

Математическое ожидание и дисперсия для показательного распределения равны

M(x)=1/l

D(x)=1/l²

Из условия

F(x_Me)=0.5=1- e^-lxMe

получим для медианы значение

x_Me=ln(0.5)/(-l)

Мода показательного распределения равна 0

Нормальное распределение

Нормальное распределение описывается законом

f(x)= 1/s/(2p)^0.5×e^-1/2×(x-a)2/s²

Данный закон распределения зависит отдвух праметров – a и s. Можно показать, что

M(x)= a

D(x)= s²

График плотности нормального распределения называют нормальной кривой (кривой Гаусса), а соответствующую функцию - функцией Гаусса. Данная функция определена для всех значений x, симметрична относительно x=a, на бесконечности она стремится к 0, максимальна при x=a, f(a)= 1/s/(2p)^0.5. Точки перегиба - x=a+s и - x=a-s.

Нормальное распределение называется нормированным при

M(x)=0

D(x)= 1

Значения