Расчет надежности при параллельном соединении элементов.
Для повышения надежности ответственной системы обычно применяют резервирование ее элементов, т.е. дублируют важные части системы. Вместо одного элемента включают одновременно несколько элементов для того, чтобы при отказе одного из них система на прекращала работу.
Предположим, что вероятность отказа основного элемента (за некоторый промежуток времени – период работы) равна 0,1. Нас интересует надежность системы, составленной из параллельно подключенных 4 одинаковых элементов. Если предположить, что отказы элементов вызываются внутренними (брак при изготовлении, усталость материала, износ и т.п.), а не внешними (повышение напряжения питания, физическое разрушение при аварии) причинами, то естественно ( в первом приближении) считать отказы разных элементов независимыми.
В качестве элементарного исхода рассмотрим двоичный вектор
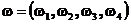
имеющий 4 координаты – соответственно состоянию каждого элемента в конце заданного промежутка времени ( 1 – исправен, 0 - отказ). Из условия задачи следует, что события , связанные с разными координатами должны быть независимы, следовательно, используя формулу
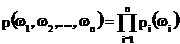
в нашем случае получаем
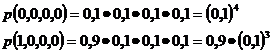
и т.д.
Система будет работоспособной весь период времени, если не отказал хотя бы один из ее элементов. Этому условию удовлетворяют все элементарные исходы, кроме одного
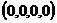
| Сообразите, как рассчитать надежность такой системы при неодинаково надежных, но независимых элементах | Таким образом, вероятность отказа всей системы равна 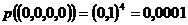 а вероятность безотказной работы (надежность) а вероятность безотказной работы (надежность) 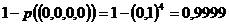 |
| Покажите ,что это действительно можно делать, если отказы элементов независимы в совокупности | Заметим, что если рассматриваемая система является частью более сложной системы, то можно при расчетах надежности заменить эти четыре элемента одним, с вероятностью отказа 0,0001. |
Расчет надежности при последовательном соединении элементов
Системой с последовательным соединением элементов назовем такую систему из n элементов, в которой отказ любого из этих элементов приводит к отказу всей системы.
Рассчитаем надежность системы, составленной из 3 последовательно соединенных одинаковых независимых элементов (вероятность отказа каждого - 0,1)
Действуя по аналогии с предыдущим примером, построим пространство элементарных исходов и определим их вероятности. Отказ системы возникает при всех исходах кроме одного
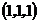
Таким образом, вероятность безотказной работы этой системы равна
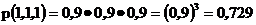
что значительно меньше чем вероятность безотказной работы одного элемента.
Заметим, что если рассматриваемая система является частью более сложной системы, то можно при расчетах надежности заменить эти три элемента одним, с вероятностью отказа 0,271.
