Функция одной случайной величины

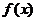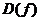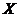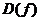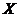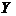Пусть дана функция одной переменной с областью определения и некоторая случайная величина , все значения которой принадлежат множеству . Тогда, если приняла значение , будем считать, что новая случайная величина приняла значение 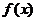. Эта новая случайная величина называется функцией случайной величины 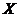, и в этом случае пишут: .

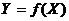Вопрос состоит в том, каков закон распределения 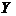, если мы знаем закон распределения .

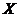Остановимся сначала на дискретной случайной величине 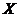, закон распределения вероятностей которой задается таблицей

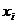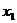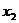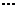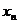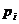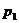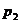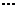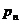Событие 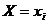происходит с вероятностью 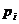, с этой же вероятностью 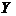примет значение 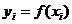. Мы имеем таблицу распределения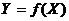

Значения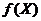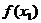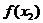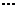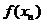
вероятности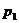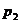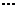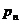

Если существует несколько значений 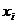, для которых 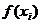принимает одно и то же значение, то все такие случаи объединяются в один, которому соответствует по теореме сложения вероятность, равная сумме вероятностей объединяемых случаев.

Пример. Пусть распределение случайной величины 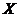задается следующим образом:

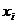	-2	-1
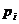	0.1	0.1	0.3	0.3	0.2

Требуется найти законы распределения случайных величин 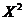и .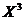

Решение. Возможные значения 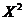: 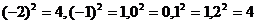. Отсюда 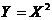принимает значения 0, 1, 4 соответственно с вероятностями 0.3; 0.1+0.3=0.4; 0.1+0.2=0.3. Таким образом, таблицей распределения 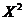будет таблица вида

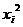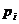	0.3	0.4	0.3

Так как функция 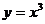- взаимно однозначная, то различным значениям 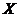отвечают различные значения 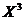и, следовательно, таблицей распределения этой случайной величины будет таблица вида

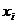	-8	-1
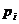	0.1	0.1	0.3	0.3	0.2

Теперь остановимся на случае, когда 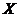- непрерывная случайная величина с плотностью распределения 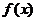. Пусть имеется монотонно возрастающая на множестве значений случайной величины 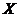функция 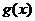( 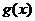- непрерывно дифференцируемая и 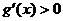). Если множество значен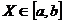ий 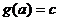и и 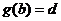,то функция распределения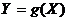

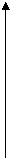
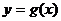
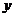
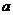0

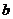
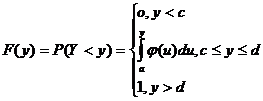. Здесь 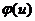– есть плотность распределения .

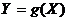Для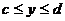

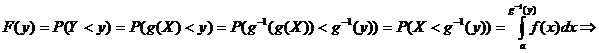
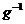( - функция, обратная к 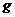на сегменте 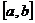). Отсюда

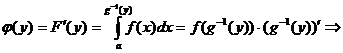
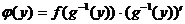
(мы воспользовались теоремой Барроу о производной от определенного интеграла с переменным верхним пределом по этому верхнему пределу).

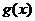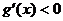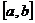Если - монотонно убывающая функция и для всех из промежутка , то для 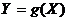функция распределения имеет вид

,

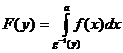а плотность - 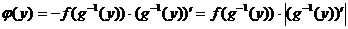, так как 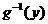- функция монотонно убывающая и ее производная отрицательная.

Пример. Пусть 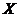принимает значения только на сегменте 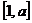с плотностью распределения 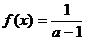. Найти плотность распределения случайной величины .

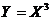Решение. 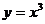– функция монотонная возрастающая, обратная к ней функция 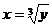, а 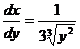. Поэтому, плотность распределения 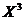будет

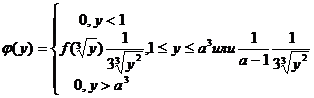
Пример. Даны две независимые случайные величины: 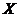– число появлений герба при двух подбрасываниях монеты и 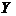– число очков, выпавших при подбрасывании игральной кости. Найти закон распределения разности .

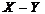Решение. Запишем законы распределения данных случайных величин 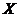и .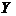

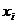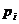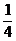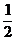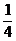и

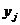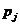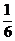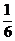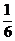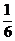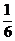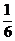Составим таблицу распределения случайной величины 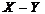, полагая .

				…	…					…	…			…	…	…	…
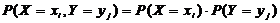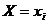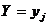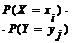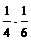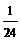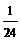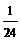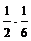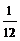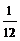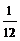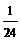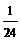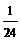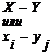	-1	-2	-3	-4	-5	-6		-1	-2	-3	-4	-5			-1	-2	-3	-4

Тогда

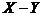	-6	-5	-4	-3	-2	-1

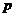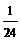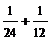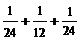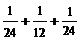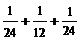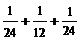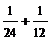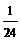или

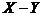	-6	-5	-4	-3	-2	-1
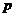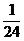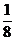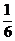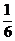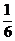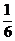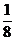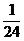