Корреляционный момент случайных величин и его свойства

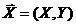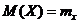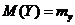Пусть имеется случайный вектор , распределение которого известно, т. е. известна таблица или плотность распределения . Тогда , . По известному закону распределения можно найти также дисперсии составляющих вектор 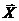. Пусть 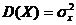и 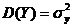. Однако математические ожидания и дисперсии случайных величин 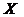и 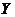недостаточно полно характеризуют случайный вектор 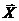, т. к. не выражают степень зависимости составляющих вектора. Эту роль выполняют корреляционный момент и коэффициент корреляции.

Корреляционным моментом 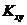случайных величин 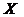и 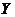называют математическое ожидание произведения отклонений этих величин от своих математических ожиданий:

.

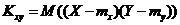Если распределение дискретное, то

.

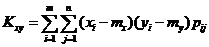При непрерывном распределении

.

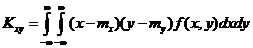Корреляционный момент обладает следующими свойствами:

1. 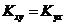– свойство симметричности. Оно очевидно.

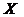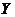2. Если и независимые случайные величины, то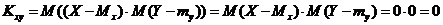

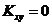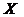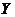Обратное, вообще говоря, не имеет места. Если , то в этом случае величины и называются некоррелированными.

3. 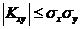. Действительно, ;

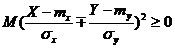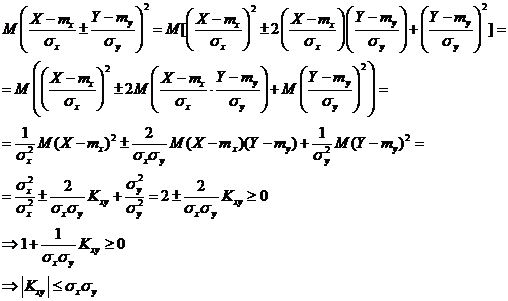
Коэффициент корреляции и его свойства

Если отклонения случайных величин заменить их нормированными отклонениями, то получим безмерную величину - коэффициент линейной корреляции :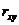

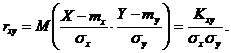
Свойства коэффициента линейной корреляции вытекают из свойств корреляционного момента:

1. ;

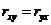2. ;

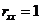3. ;

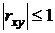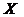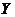4. Если и – независимые случайные величины, то ;

5. Если 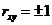то между 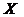и 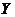существует линейная функциональная зависимость. Доказательство проведем для случая :

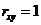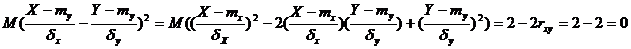
Получили, что математическое ожидание неотрицательной величины равно нулю, сама эта величина - тождественный нуль:

,

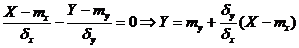что и требовалось доказать.

Формула Бернулли

Пусть некоторый опыт воспроизводится 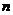раз и каждый раз событие может наступать с одной и той же вероятностью 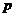, независимо от результатов предыдущих опытов. В этом случае говорят о повторных независимых испытаниях. При этом событие может наступать 0, 1, 2, … , 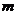, … , 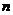раз. Число наступлений события – это случайная величина. Найдем вероятность, с которой событие наступит 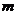раз. Эту вероятность обычно обозначают символом 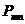. Интересующее нас событие – наступление 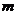раз в 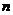испытаниях, можно разбить на частные случаи, каждый из которых определяется номерами тех испытаний, в которых наступает . 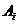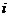Пусть - это наступление в -ом испытании. Набор таких 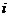определяет отдельный случай. Например, ( 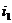, ,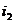…, 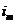)- это случай, когда наступило в 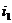-ом испытании, затем 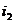-ом и т.д., во всех же остальных испытаниях не наступило. Всех случаев будет столько, сколькими способами мы можем выбрать m натуральных чисел из 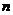(1,2,3,…, 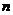), т. е. число всех случаев – это число сочетаний из 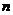элементов по :

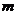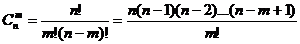
Найдем вероятность отдельного случая. Чтобы он наступил, должны наступить события 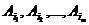и события 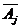, где 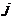пробегает те числа из 1,2,3,…, 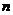, которые отличны от 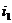, ,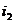…, 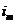. Так как все указанные события независимы и операция умножения событий коммутативна, то вероятность отдельного случая

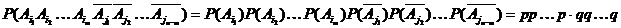
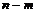
где .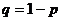

Мы видим, что все частные случаи равновозможны, поэтому, применяя теорему сложения для несовместных событий, получаем

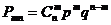- формула Бернулли.

Пример. Пусть всхожесть семян ржи составляет 90%. Чему равна вероятность того, что из 7 посеянных семян взойдет 5?

Решение. Вероятность всхожести отдельного семени 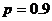, следовательно, 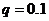. По формуле Бернулли находим вероятность

.
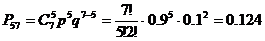