Теорема гипотез. ( Формула Байеса )

Следствием теоремы умножения и формулы полной вероятности является так называемая гипотез, или формула Байеса. Поставим следующую задачу.

Имеется полная группа несовместных гипотез 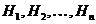. Вероятности этих гипотез до опыта известны и равны соответственно 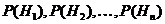. Произведен опыт, в результате которого наблюдено появление некоторого события . Спрашивается, как следует изменить вероятности гипотез в связи с появлением этого события?

Здесь, по существу, речь идет о том, чтобы найти условную вероятность 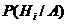для каждой гипотезы.

Из теоремы умножения имеем:

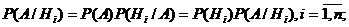
или, отбрасывая левую часть,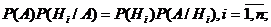

откуда

,

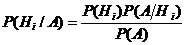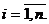
Выражая Р(А) с помощью формулы полной вероятности, имеем

,

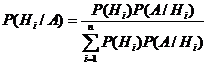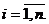
Пример. Два стрелка независимо один от другого стреляют по одной мишени, делая каждый по одному выстрелу. Вероятность попадания в мишень для первого стрелка 0,8, для второго - 0,4. После стрельбы по мишени обнаружена одна пробоина. Найти вероятность того, что эта пробоина принадлежит первому стрелку.

Решение. До опыта возможны следующие гипотезы:

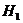- ни первый, ни второй не попадут;

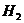- оба попадут;

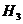- первый попадет, второй - нет;

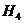- первый не попадет, второй попадет.

Вероятность этих гипотез:

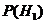=0,2×0,6=0,12; 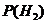=0,32; 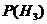=0,8×0,6=0,48; 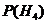=0,2×0,4=0,08.

Условные вероятности наблюденного события при этих гипотезах:

; ; ; .

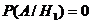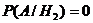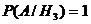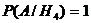После опыта невозможные гипотезы ¾ 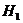и .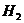

^.

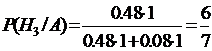13. Дискретные и непрерывные случайные величины

Как уже было сказано, случайной величиной называется величина, которая в результате опыта может принять то или иное значение, не известно заранее, какое именно. Различают величины дискретного и непрерывного типа. Возможные значения дискретной величины могут быть заранее перечислены.

Возможные значения непрерывной величины не могут быть заранее перечислены и непрерывно заполняют некоторый промежуток.

Примеры дискретных случайных величин:

- число появлений герба при 3-х бросаниях монеты: 0, 1, 2, 3;

- число отказавших элементов в приборе, состоящем из пяти элементов-0,1,2,3,4,5;

- число попаданий в самолет, достаточное для вывода его из строя-1,2,3,…, ,…;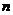

- число сбитых в воздушном бою самолетов-0,1,2,…, 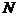; где 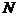-общее число боевых самолетов.

Примеры непрерывных случайных величин:

- абсцисса (ордината) попадания при выстреле;

- расстояние от точки попадания до центра мишени;

- ошибка измерителя высоты;

- время безотказной работы радиолампы.

Будем обозначать случайные величины большими буквами 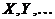, а их возможные значения - соответствующими малыми буквами. Например, - число попаданий при 3-х выстрелах; возможные значения - .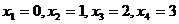

Рассмотрим дискретную случайную величину с возможными значениями 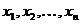. может принимать любое из этих значений с некоторой вероятностью. В результате опыта произойдет одно из полной группы событий 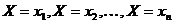. Вероятности этих событий обозначим буквой 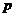с соответствующими индексами –

.

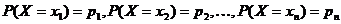Т.к. эти несовместные события образуют полную группу, то .

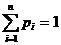Закон распределения

Эта суммарная вероятность каким-то образом распределена между отдельными значениями. Случайная величина будет полностью описана, с вероятностной точки зрения, если мы зададим это распределение, т.е. в точности укажем, какой вероятностью обладает каждое из событий 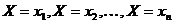. Этим мы установим так называемый закон распределения случайной величины.

Законом распределения случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями. Про случайную величину будем говорить, что она подчинена данному закону распределения.

Формой задания закона является таблица

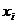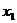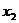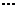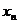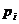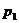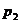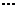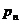Такую таблицу мы будем называть рядом распределения случайной величины X.

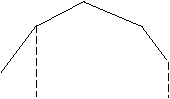
Графическое изображение ряда распределения называется многоугольником распределения .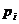

			Полигон распределения

p₁

x_i

x₁ x₂ x₃ … x_n

Многоугольник распределения - также одна из форм закона распределения.

Функция распределения

Мы рассмотрели закон распределения дискретной случайной величины. Для непрерывной случайной величины такую характеристику построить нельзя. Непрерывная случайная величина имеет бесчисленное множество возможных значений, сплошь заполняющих некоторый промежуток (несчетное множество). Для непрерывной случайной величины не существует ряда распределения, как он существует для дискретной величины. Но различные области возможных значений случайных величин все же не является одинаково вероятными, и для непрерывной величины существует распределение вероятностей, хотя и не в том смысле, как для прерывной.

Для количественной характеристики, этого распределения вероятностей удобно воспользоваться не вероятностью события 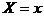, а вероятностью события 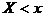, где – некоторая текущая переменная. Вероятность этого события есть некоторая функция от . Эта функция называется функцией распределения случайной величины и обозначается , .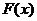

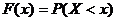Функцию распределения 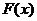иногда называют также интегральной функцией распределения или интегральным законом распределения. Функция распределения есть самая универсальная характеристика случайной величины. Она существует для всех случайных величин: как дискретных, так и непрерывных. Функция распределения полностью характеризует случайную величину с вероятностной точки зрения, т. е. является одной из форм закона распределения.