Дифференциальные уравнения с разделяющимися переменными.

Уравнением с разделяющимися переменными (тип I) называются уравнения вида

, , .

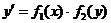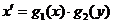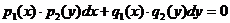Чтобы решить уравнение типа I надо разделить переменные, привести уравнение к виду с разделенными переменными 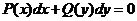и проинтегрировать почленно.

? ?

Как разделять переменные?

Для отыскания решения уравнения 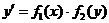или 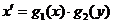нужно разделить в нем переменные. Для этого

1. заменим ,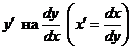

2. умножим обе части уравнения 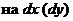( 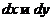должны быть только в числителях),

3. разделим обе части уравнения на такое выражение, чтобы в одну часть уравнения входило только x, в другую – только y, т. е. ,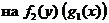

4. проинтегрируем обе части.

При делении обеих частей уравнения на выражение, содержащее неизвестные x и y, могут быть потеряны решения (особые), обращающие это выражение в нуль.

Пусть дифференциальное уравнение задано в дифференциальной форме (1.4). В частном случае, когда каждая из функций 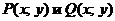является произведением двух функций, одна из которых – функция только x, а вторая – только y, т. е. когда

,

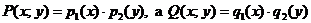уравнение примет вид .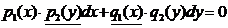

Разделение переменных производится делением обеих частей полученного уравнения на произведение 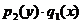, в котором 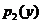− функция только 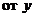, являющаяся множителем 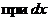, а 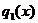− функция только 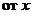, являющаяся множителем .

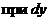После деления на это произведение уравнение примет вид .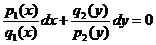

Это уравнение называется уравнением с разделенными переменными: 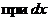находится функция, зависящая только 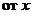, 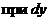− только .

! !

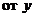1.2.2. Однородные дифференциальные уравнения (тип )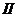

Функция 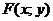называется однородной функцией измеренияk относительно аргументов x и y, если равенство 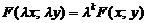справедливо для любого 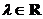, при котором функция 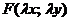определена, .

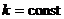Дифференциальное уравнение в нормальной форме 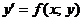называется однородным относительно переменных x и y, если 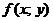− однородная функция нулевого измерения относительно своих аргументов, т. е. .

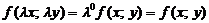Однородное дифференциальное уравнение в нормальной форме всегда можно записать в виде (положив ) .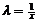

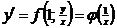Уравнение в дифференциальной форме 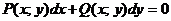называется однородным, если функции 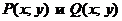− однородные функции одного измерения.

Однородное уравнение с помощью замены 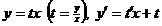сводится к уравнению с разделяющимися переменными относительно 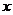и новой функции .

? ?

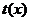Чтобы решить однородное уравнение, нужно:

1.Ввести подстановку 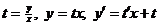сводится к уравнению типа I.

2. Разделить переменные и проинтегрировать уравнение типа I.

3. Результат интегрирования упростить, пропотенцировать, если нужно, и записать общий интеграл, вернувшись к исходной переменной.

! !

Линейные дифференциальные уравнения

Дифференциальное уравнение называется линейным, если функция, ее производная входят в него в первой степени (линейно): 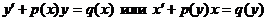− тип III.

Для решения уравнения типа III применяется метод подстановки

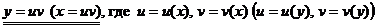− непрерывные функции,

а также метод вариации произвольной постоянной.

? ?

Что необходимо для решения линейных уравнений:

Уметь:

1.интегрировать по частям .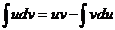

2. заменять переменную 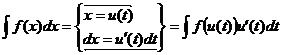,