Второй замечательный предел, его применение в финансовых вычислениях.

Предел последовательности 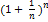при n → ∞ называется вторым замечательным пределом. Этот предел равен числу е: 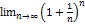= е = 2, 71

Положив а_n = 1 /п, получим 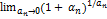= e

Доказательство.Зная, что второй замечательный предел верен для натуральных значений x, докажем второй замечательный предел для вещественных x, то есть докажем, что 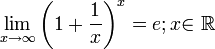. Рассмотрим два случая:

1. Пусть 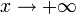. Каждое значение x заключено между двумя положительными целыми числами: 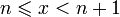, где 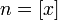— это целая часть x.

Отсюда следует: 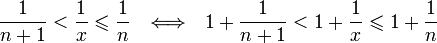, поэтому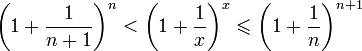

Если 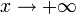, то 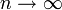. Поэтому, согласно пределу 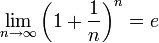, имеем: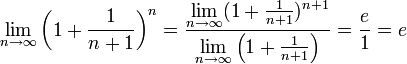

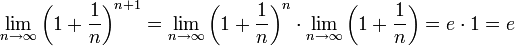
По признаку (о пределе промежуточной функции) существования пределов .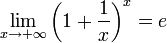

2. Пусть 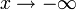. Сделаем подстановку − x = t, тогда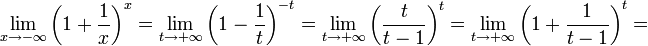

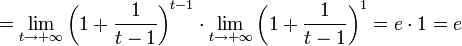
Из двух этих случаев вытекает, что 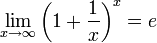для вещественного x.

Билет №12

Общие понятия о сравнении бесконечно малых функций.

Отношение бесконечно малых величин образует так называемую неопределённость 0/0.

Определения. Допустим, у нас есть бесконечно малые при одном и том же 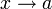величины α(x) и β(x) (либо, что не важно для определения, бесконечно малые последовательности).

Если 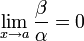, то β — бесконечно малая высшего порядка малости, чем α. Обозначают β = o(α).

Если 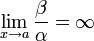, то β — бесконечно малая низшего порядка малости, чем α. Соответственно α = o(β).

Если 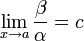(предел конечен и не равен 0), то α и β являются бесконечно малыми величинами одного порядка малости.
Это обозначается как β = O(α) или α = O(β) (в силу симметричности данного отношения).

Если 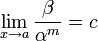(предел конечен и не равен 0), то бесконечно малая величина β имеет m-й порядок малости относительно бесконечно малой α.

Теорема о промежуточных значениях. Если функция f(x) непрерывна на отрезке [a;b] и f(a) ≠ f(b), то для каждого значения y, заключенного между f(a) и f(b), найдется точка x 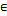[a;b] (и возможно, не одна) такая, что f(x) = y.

Билет №13

Непрерывность функции в точке и на отрезке.

Функция f(x) называется непрерывнойв точке х₀, если эта функция определена в некоторой окрестности точки х₀ и существует предел 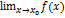, равный f(x₀).

Если при каком-либо значении х₀ не выполняются указанные усло­вия, то точка х₀ называется точкой разрыва функции f(x).

Если функция непрерывна в каждой точке некоторого промежутка, то она непрерывна на этом промежутке.

Если выполняется равенство f(x₀ - 0) = f(x₀), то говорят, что функция f(x) непрерывна слева в точке х₀. Аналогично, если f(x₀ + 0) = f(x₀), то функция непрерывна справа в точке х₀.

Функцию f(x) называют непрерывной на отрезке [a;b], если она непрерывна в каждой точке интервала (a; b) и, кроме того, непрерывна справа в точке a и слева в точке b .

Теорема Коши о нулях непрерывной функции. Только на одном из отрезков – [a₃;b ₃] – имеется нуль функции, так как на этом отрезке функция непрерывна и принимает значения разных знаков на концах.

Теорема Коши. Если функция f(x) непрерывна на отрезке [a;b] и принимает на его концах значения разных знаков, то на отрезке [a;b] имеется хотя бы один нуль функции f. При этом, если функция строго монотонна на этом отрезке, то она принимает значение 0 лишь один раз.

Билет №14