Частные производные второго порядка

Пусть функция 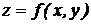имеет частные производные первого порядка 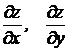. Так как производные являются функциями аргументов х и у, то можно найти производные от этих функций. Частные производные этих функций называются частными производными второго порядка (вторыми частными производными) данной функции .

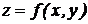Так, для функции z = f(x, у) двух аргументов х и у (предполагается, что все производные первого порядка существуют) частные производные второго порядка:

.

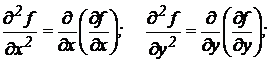
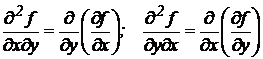Частные производные 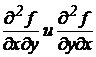называются смешанными частными производными второго порядка.

Решение задач

Пример 3.1. Найти частные производные функций:

1). ;

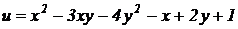2). .

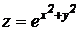Решение. 1) рассматривая у как постоянную величину, получим 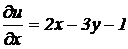, рассматривая х как постоянную величину, найдем: .

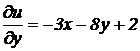2) пусть 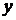– const, получим ,

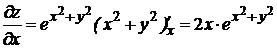пусть х – const, получим .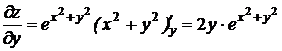

Пример 3.2. Реакция на инъекцию х единиц лекарственного препарата описывается функцией 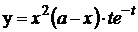, где t выражается в часах с момента инъекции, a – некоторая константа. Найти частные производные .

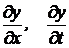Решение. Найдем частные производные

;

.

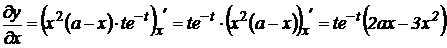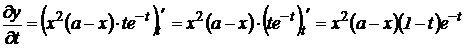Пример 3.3. Для функции 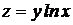найти производные второго порядка.

Решение. Найдем частные производные первого порядка , .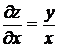

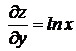Дифференцируя повторно, получим:

.

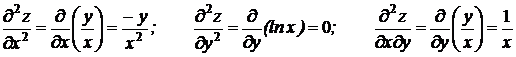Пример 3.4. Найти полный дифференциал функций:

1). ;

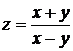2). .

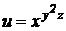Решение. 1) Найдем частные производные

;

.

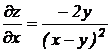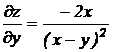Следовательно, .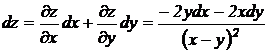

2) найдем частные производные по переменным х, у и z:

, , ,

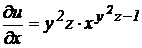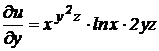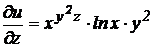следовательно

.

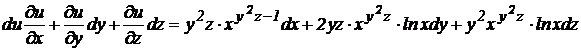Примеры для самостоятельного решения

Найти частные производные функций:

1. .

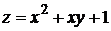2. .

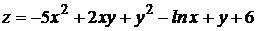3. .

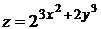4. .

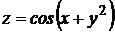Найти все частные производные второго порядка функции:

5. .

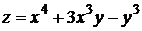6. .

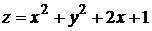Найти частные и полный дифференциал для следующих функций:

7. .

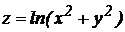8. .

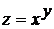9. .

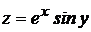10. .

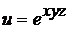Задание на дом

Практика

Найти все частные производные функций:

1. .

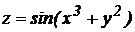2. .

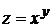3. .

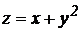4. .

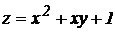Найти частные и полный дифференциал для следующих функций:

5. .

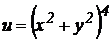6. .

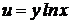7. .

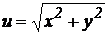8. .

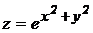Теория

1. Лекция по теме «Неопределенный интеграл. Основные свойства неопределенного интеграла. Основные способы интегрирования».

2. Занятие 4 данного методического пособия.

3. Павлушков И.В. и другие стр. 122-144.

Занятие 4. Неопределенный интеграл и его основные свойства. Основные методы интегрирования.

Актуальность темы: понятие неопределенного интеграла является одним из ключевых понятий математического анализа. Методы интегрирования позволяют решать задачу восстановления функции по ее производной, которая находит широкое применение в естественнонаучных дисциплинах.

Цель занятия: закрепление понятия неопределенного интеграла; овладение способами и методами интегрирования.

Целевые задачи:

знать: понятие первообразной функции, определение неопределенного интеграла, основные свойства неопределенного интеграла; свойства интеграла; сущность методов интегрирования;

уметь: применять основные формулы интегрирования при нахождении интегралов методом непосредственного интегрирования; использовать свойство инвариантности неопределенного интеграла, применять методы интегрирования.

Краткие сведения из теоретического курса

Основные понятия

Восстановление функции по известной производной этой функции основная задача интегрального исчисления (т.е. найти функцию F(x), зная ее производную или дифференциал).

Первообразной функцией для данной функции f(x) на интервале называется такая функция F(x), производная которой равна f(x) или дифференциал которой равен f(x)dx на рассматриваемом интервале.

Теорема. Если функция F(x) является первообразной для функции f(x) на некотором интервале, то множество всех первообразных для f(x) задается формулой F(x)+C, где С – постоянное число:

.

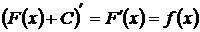Множество всех первообразных функций F(x)+C для f(x) или f(x)dx называется неопределенным интегралом от функции f(x) и обозначается 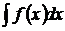. Таким образом можно записать 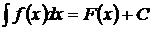, если F’(x)=f(x).

Свойства неопределенного интеграла

1. Производная от неопределенного интеграла равна подынтегральной функции, т. е. .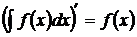

2. Дифференциал от неопределенного интеграла равен подынтегральному выражению, т.е. .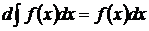

3. Интеграл от дифференциала первообразной равен самой первообразной и дополнительному слагаемому С, т. е.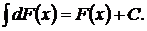

4. Постоянный множитель не равный нулю можно вынести за знак неопределенного интеграла, т. е.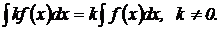

5. Интеграл от алгебраической суммы конечного числа функций равен алгебраической сумме интегралов от слагаемых, т. е.

.

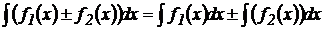Таблица простейших интегралов

1. ;

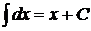2. ;

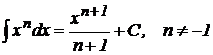3. 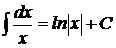, при ;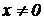

4. , ;

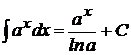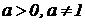5. ;

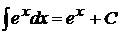6. ;

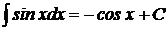7. ;

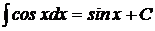8. ;

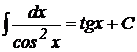9. ;

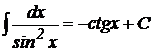10. .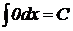