Метод непосредственного интегрирования

Метод непосредственного интегрирования, при котором данный интеграл путем тождественных преобразований подынтегральной функции и использовании свойств неопределенного интеграла приводится к одному или нескольким табличным интегралам.

Метод замены переменной (подстановки)

Этот способ заключается в переходе от данной переменной интегрирования к другой переменной для упрощения подынтегрального выражения и приведения его к табличному виду. В интеграле 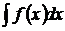сделаем подстановку 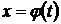, где функция 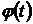имеет непрерывную производную. Тогда: 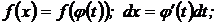на основании независимости неопределенного интеграла от выбора аргумента: 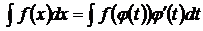– формула замены переменных в неопределенном интеграле. Иногда целесообразно подбирать подстановку в виде 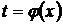, тогда 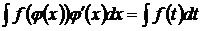, где .

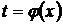Метод интегрирования по частям

Интегрирование по частям состоит в том, что подынтегральное выражение заданного интеграла представляется каким-либо образом в виде произведения двух сомножителей u и dv (это, как правило, можно осуществить несколькими способами); затем, после нахождения v и du, используется формула интегрирования по частям.

Если u=u(x) и v=v(x) – дифференцируемые функции, тогда d(uv)=vdu+udv, откуда udv=d(uv)-vdu. Интегрируя последнее выражение, получаем: 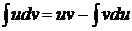– формула интегрирования по частям, которая применяется в тех случаях, если интеграл в правой части более прост, чем исходный. Эта формула дает возможность свести вычисление интеграла 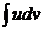к вычислению интеграла 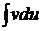, который может оказаться существенно более простым, чем исходный.

Решение задач

Пример 7.1. Найти интегралы:

1) 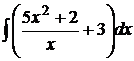. 2) .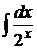

Решение. 1) Применяя свойства 4 и 5 неопределенного интеграла, а также алгебраические преобразования сведем интеграл к трем табличным интегралам:

;

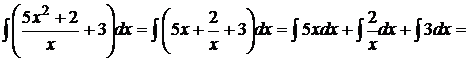
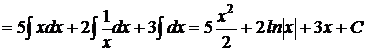2) Учитывая, что 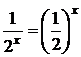и используя основные формулы интегрирования, имеем: .

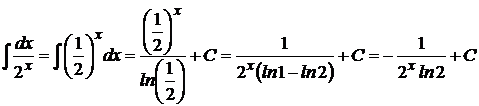Пример 7.3. Найти интегралы:

1) 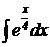. 2) .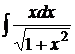

Решение. 1) Введем замену: пусть x=4t, тогда dx=d(4t)=4dt. Следовательно, можем записать:

.

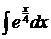
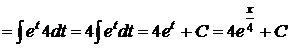2) Положим 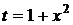. Тогда 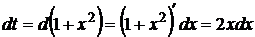, следовательно 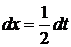. Можем записать:

.

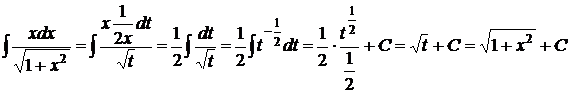Пример 7.4. Найти интеграл .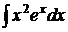

Решение. Интеграл будем искать методом интегрирования по частям. Положим 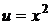, 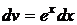; тогда 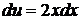, 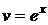. Применяем формулу интегрирования по частям: .

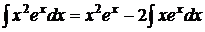Мы добились понижения степени х на единицу. Чтобы найти 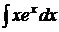, применим ещё раз интегрирование по частям. Пусть 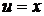, 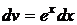; тогда 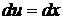, 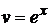и можно записать

.

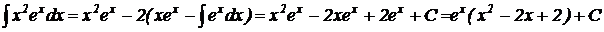Пример 7.5. Найти интегралы:

1) .

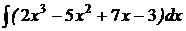2) .

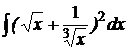3) .

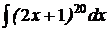4 ;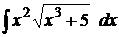

5) .

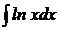Решение: 1). Применим метод непосредственного интегрирования: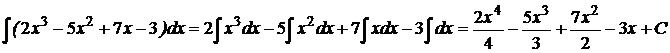

2). Воспользуемся формулой сокращенного умножения для преобразования подынтегральной функции и применим метод непосредственного интегрирования:

.

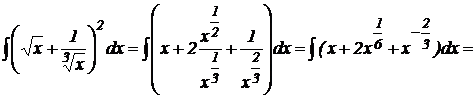
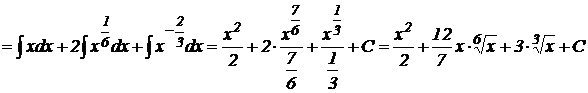3). Этот интеграл можно найти с помощью замены переменной. Полагая 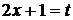, имеем 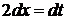, т.е. 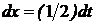. Отсюда получим

.

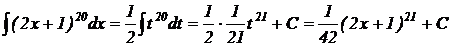4). Введем подстановку: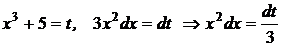

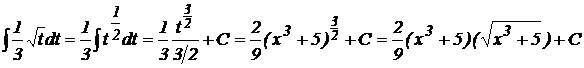
5). Применим метод интегрирования по частям. Пусть 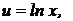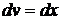; тогда 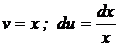. Используя формулу интегрирования по частям, получим .

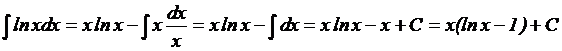Пример 7.6. Найти закон изменения скорости тела, если уравнение ускорения имеет вид: 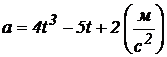и, если известно, что скорость тела через 2 секунды была равна 10 .

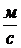Решение: Так как ускорение движения тела есть первая производная скорости движения по времени, то имеет место формула 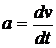. Следовательно, можно записать 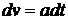. Проинтегрировав данное соотношение, получим 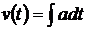. Тогда .

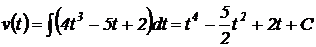Исходя из начальных условий: при 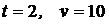, найдем С:

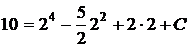Þ .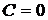

Итак, уравнение скорости движения тела .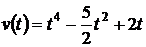

Самостоятельная работа студентов на занятии.

Найти интегралы

1. .

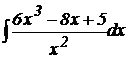2. .

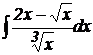3. .

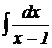4. .

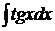5. .

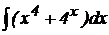6. .

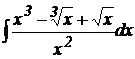7. .

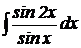8. .

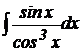9. .

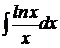10. .

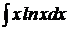11. .

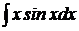Задание на дом.

6.1. Практика:

6.1.1. Найти интегралы:

1. .

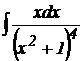2. .

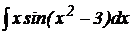3. .

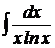4. .

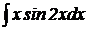5. .

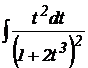6.

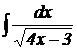
Теория.

1. Лекция по теме «Понятие определенного интеграла. Формула Ньютона-Лейбница. Приложение определенного интеграла к решению прикладных задач».

2. Занятие 5 данного методического пособия.

3. Павлушков И.В. и другие стр. 157-177.

Занятие 5. Определенный интеграл и его основные свойства. Приложения определенного интеграла.

Актуальность темы: понятие определенного интеграла широко используется в математике и других науках для вычисления площадей плоских фигур, работы переменной силы и т.п.

Цель занятия: освоить методы вычисления определенного интеграла, решения прикладных задач.

Целевые задачи:

знать: понятие определенного интеграла, свойства определенного интеграл, формулу Ньютона-Лейбница, определенный интеграл с переменным верхним пределом;

уметь: вычислять определенный интеграл, пользуясь формулой Ньютона-Лейбница; применять методы интегрирования для вычисления определенного интеграла, решения прикладных задач.

Краткие сведения из теоретического курса.

Определенный интеграл как предел интегральной суммы

Пусть функция y=f(x) определена на отрезке [a, b], a<b. Выполним следующие действия: разобьем отрезок [a, b] точками а=х₀,х₁…,х_n=b (х₀<х₁<…<х_n) на n частичных отрезков [x₀, x₁], [x₁, x₂],… [x_n-1, x_n]; в каждом частичном отрезке [x_i-1, x_i] возьмем произвольную точку с_i и вычислим f(c_i); умножим f(c_i) на длину соответствующего частичного отрезка Dx_i=x_i–x_i-1: f(c_i)Dx_i и составим сумму всех таких произведений. Сумма всех таких произведений 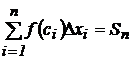называется интегральной суммой функции y=f(x) на отрезке [a, b]. Найдем предел интегральной суммы, когда n® ∞ или maxDx_i®0.

Если при этом интегральная сумма имеет предел I, который не зависит от способа разбиения отрезка на частичные отрезки, ни от выбора в них, то число I называют определенным интегралом и обозначается .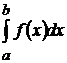

Таким образом, .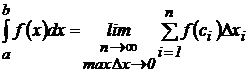

Числа а и b называются, соответственно, нижним и верхним пределами интегрирования, f(x) – подынтегральной функцией, х – подынтегральной функцией, отрезок [a, b] – областью (отрезком) интегрирования.

Функция у= f(x), для которой на отрезке [a, b] существует определенный интеграл 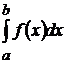, называется интегрируемой на этом отрезке.